Просмотр содержимого документа
«Практическая работа по теме: «Синус, косинус и тангенс угла»»
Практическая работа по теме: «Синус, косинус и тангенс угла»
Теоретический блок
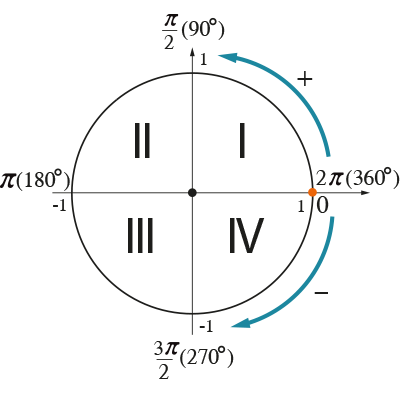
В системе координат построим полуокружность радиуса 1 с центром в начале координат.
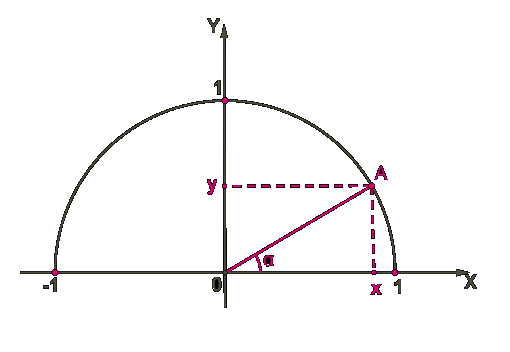
Как уже известно, в прямоугольном треугольнике синус острого угла определяется как отношение противолежащего катета к гипотенузе, а косинус острого угла определяется как отношение прилежащего катета к гипотенузе.
В треугольнике AOX:
sinα =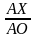 ; cosα =
; cosα =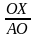 .
.
Так как радиус полуокружности R = AO = 1, то sinα = AX; cosα = OX.
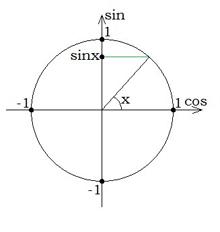
Длина отрезка AX равна величине координаты y точки A, а длина отрезка OX равна величине координаты x точки A:
A(cosα; sinα).
Следовательно, для углов 0° ≤ α ≤ 180° видно, что −1 ≤ cosα ≤ 1;
0 ≤ sinα ≤ 1.
Длина отрезка AX равна величине координаты y точки A, а длина отрезка OX равна величине координаты x точки A:
A(cosα; sinα).
Следовательно, для углов 0° ≤ α ≤ 180° видно, что −1 ≤ cosα ≤ 1;
0 ≤ sinα ≤ 1.
В прямоугольном треугольнике тангенс острого угла равен отношению противолежащего катета к прилежащему катету, а значит,
tgα =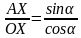 .
.
Используя единичную полуокружность и рассмотренную информацию, определим синус, косинус и тангенс для 0°; 90°; 180°.
sin0°=0;
cos0°=1;
tg0°=0;
sin90°=1;
cos90°=0;
tg90° не существует;
sin180°=0;
cos180°=−1;
tg180°=0.
Практическая часть
Задание 1. Используя единичную окружность, определите синус, косинус и тангенс для 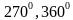 .
.
Задание 2. Найти координаты точки единичной окружности, полученной поворотом точки (1; 0) на заданный угол: 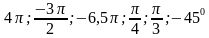 .
.
Задание 3. Построить на единичной окружности точки, соответствующие числу α, если:
 .
.






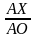 ; cosα =
; cosα =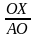 .
.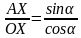 .
.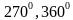 .
.
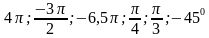 .
. .
.









