.
Практическая работа №2
«Построение углов»
Цели работы:
Познакомиться с алгоритмом построения угла заданной градусной меры.
Научиться строить угол заданной градусной меры.
Научиться определять вид угла.
Оборудование: транспортир, линейка, карандаш.
Ход работы
| Понятие «градуса» и появление первых инструментов для измерения углов связывают с развитием цивилизации в древнем Вавилоне. Хотя само слово градус имеет латинское происхождение (градус – от лат. gradus – “шаг, ступень”). Предполагают, что создание транспортира было связано с созданием первого календаря. Древние вавилонские математики и астрономы полный оборот (окружность) разделили на столько частей, сколько дней в году. Они думали, что в году 360 дней. Поэтому круг, обозначающий год, они разделили на 360 равных частей. Такое изображение было очень удобным. На нём можно было отмечать каждый прошедший день, и видеть, сколько дней осталось до конца года. Каждой части дали название – градус. Каждый градус разделили на 60 минут, а минуту – на 60 секунд. Градусная мера сохранилась и до наших дней.
| 
|
| Для измерения углов применяют транспортир. Транспортир состоит из линейки (прямолинейной шкалы) и полуокружности (угломерной шкалы). Центр этой полуокружности отмечен на транспортире или штрихом, или отверстием. Штрихи шкалы транспортира делят полуокружность на 180 долей. В некоторых моделях – на 360 долей – это круглые транспортиры.
|

|
| Если из центра этой полуокружности провести лучи через каждый штрих, то получится 180 углов. Каждый, из которых равен 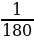 доле развернутого угла. доле развернутого угла. Такие углы принято называть градусами. Каждое деление шкалы транспортира равно 1°. Кроме делений по 1° на шкале транспортира есть ещё деления по 5° и по 10°.
| 
|
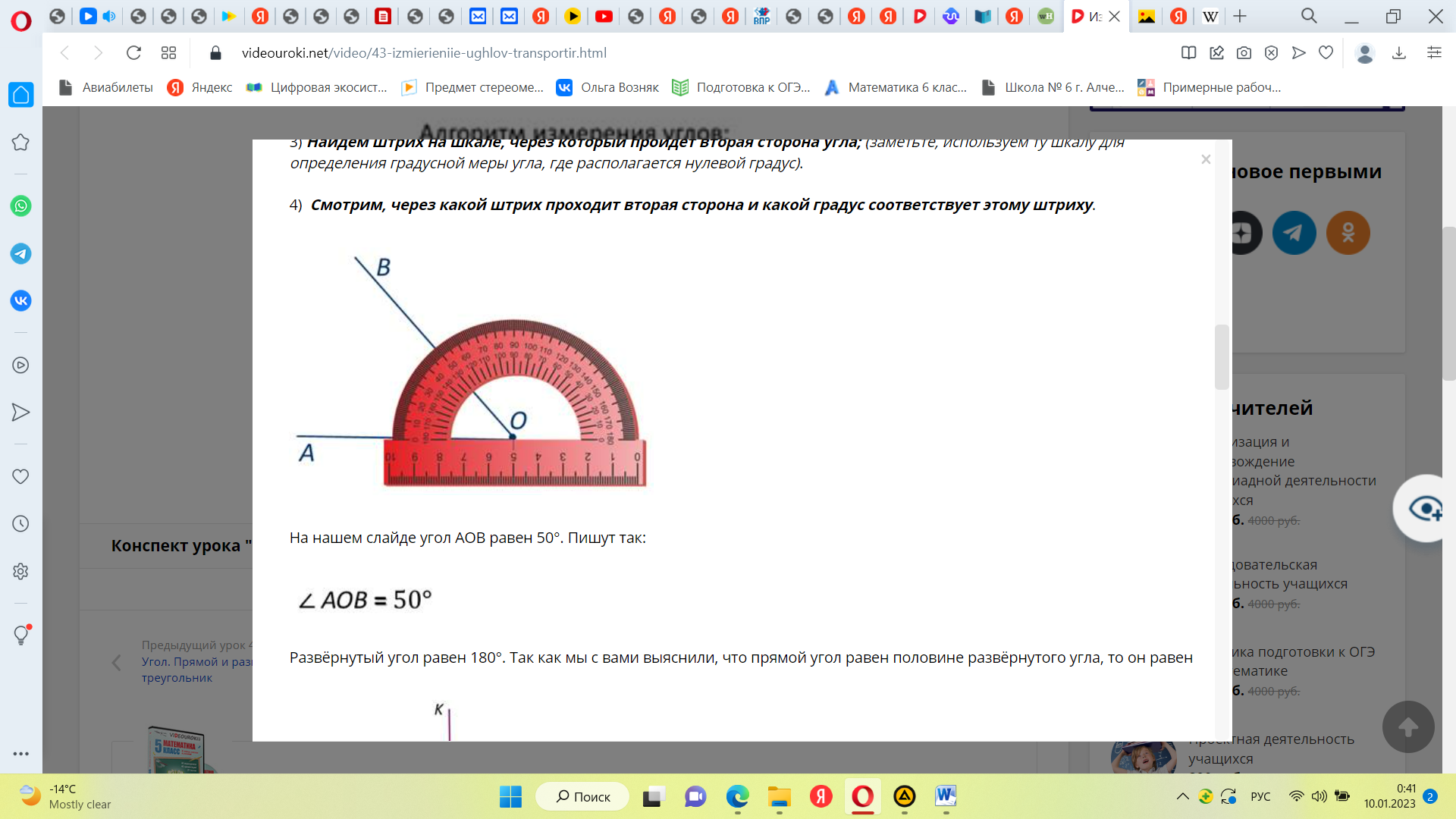
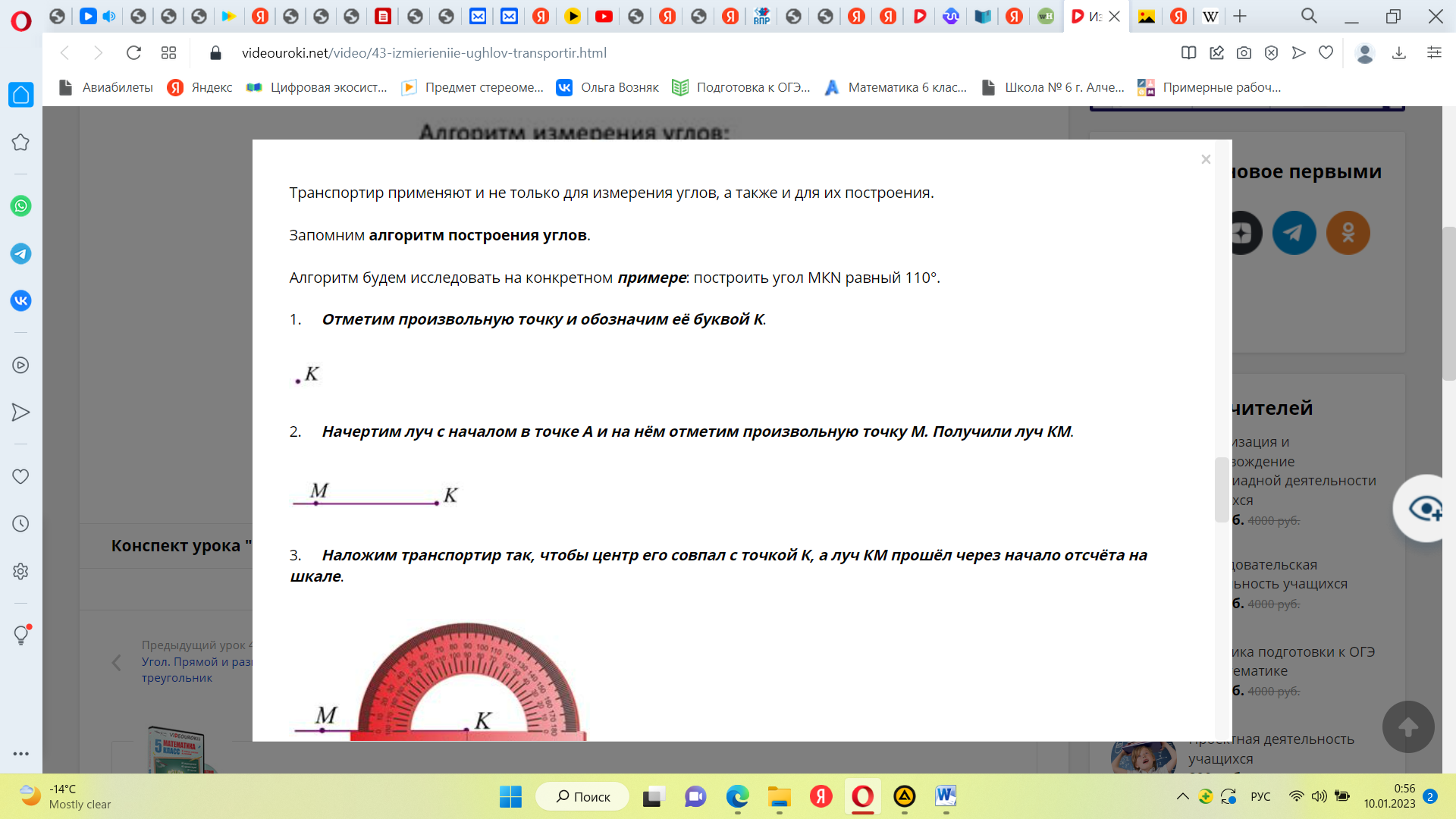
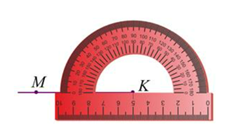
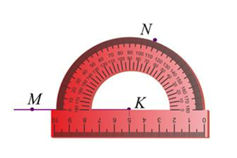
| 1) Совместить вершину угла с центром транспортира. 2) Расположить транспортир так, чтобы одна из сторон угла проходила через начало отсчёта на шкале транспортира; 0 – начало отсчёта. 3) Найдём штрих на шкале, через который пройдёт вторая сторона угла (заметьте, используем ту шкалу для определения градусной меры угла, где располагается нулевой градус). 4) Смотрим, через какой штрих проходит вторая сторона и какой градус соответствует этому штриху.
|
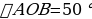
|
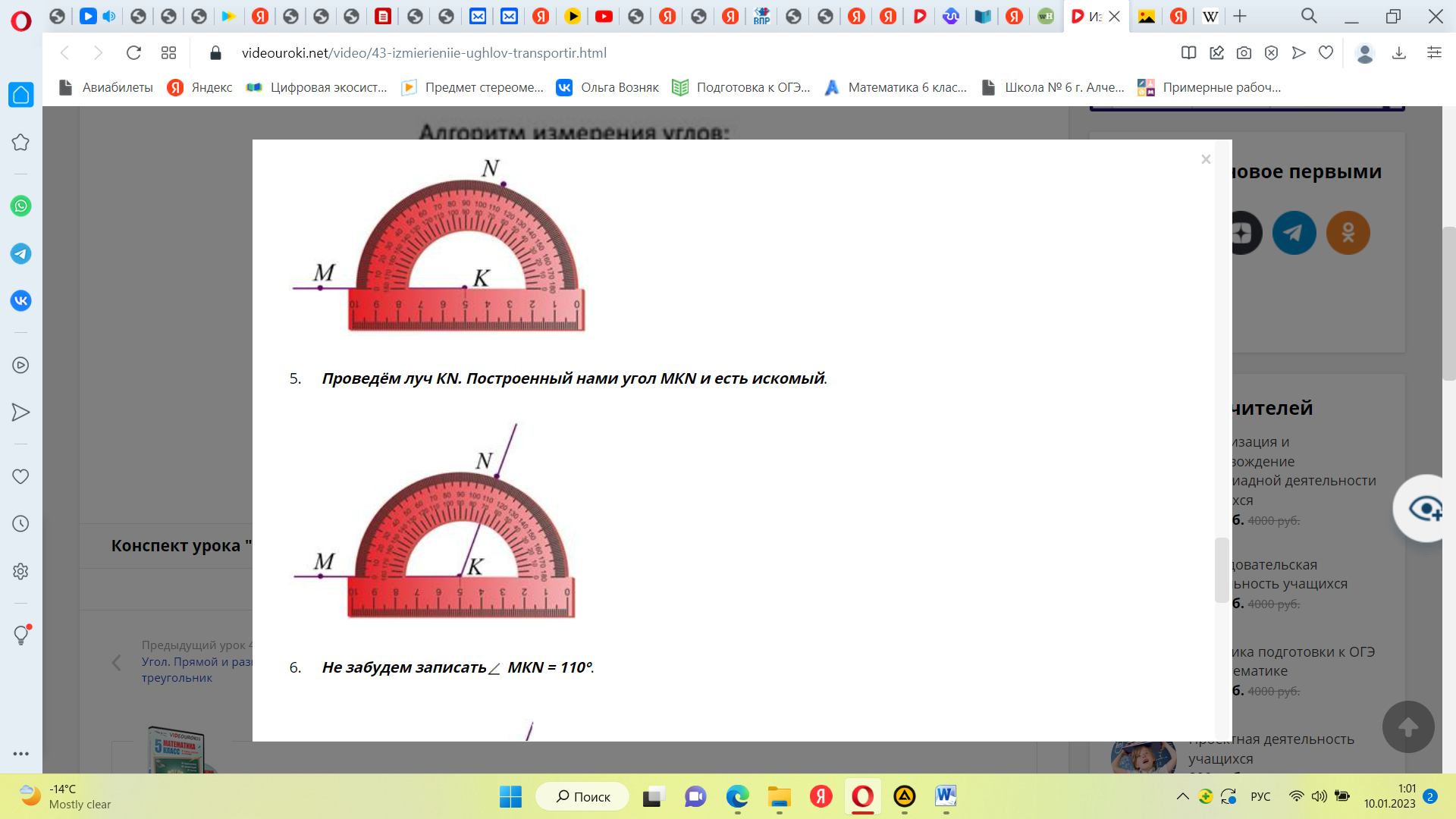
Построить угол МКN равный 110°.
Задание 1.
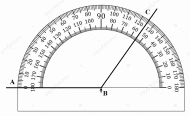
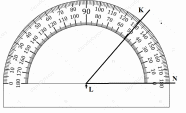
Запишите величины углов, изображенных на рисунках:
Задание 2.
Обозначьте, измерьте углы и запишите результаты измерений:
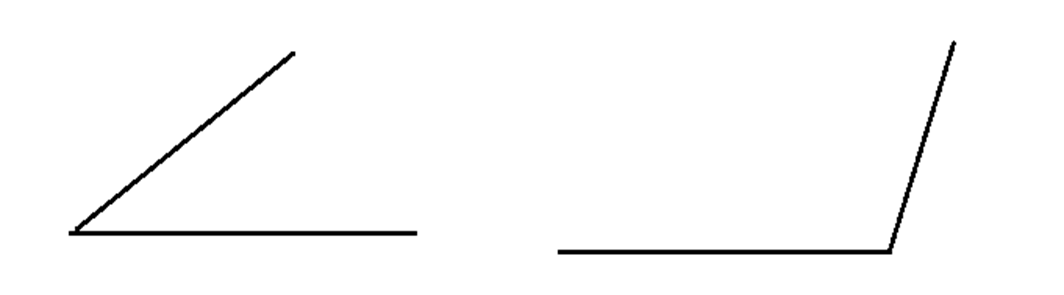
Задание 3.
Простройте:  КLM = 75°
КLM = 75°  DRS = 160
DRS = 160
Задание 4.
Назовите все углы, изображенные на рисунке:
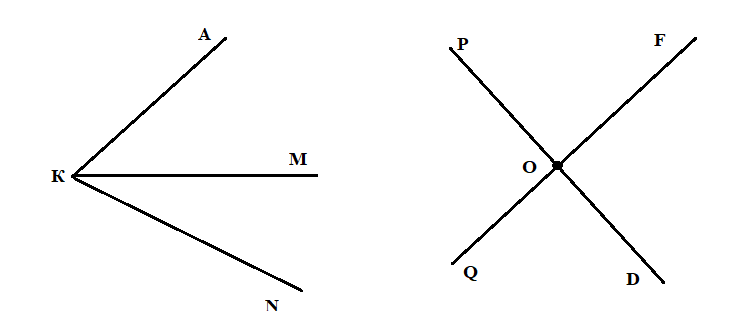
Задание 5.
Найдите величину углов:
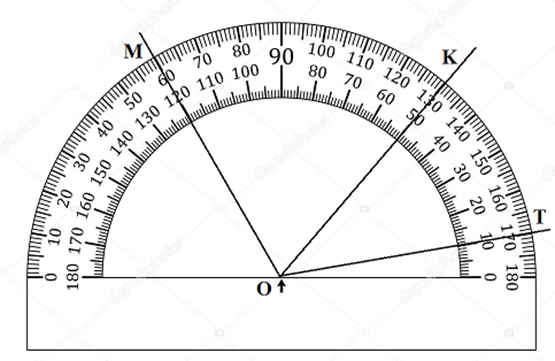
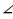 MOK=_________
MOK=_________ 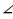 KOT = __________
KOT = __________ 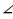 MOT =_____________
MOT =_____________
Задание 6.
Какой угол образуют часовая и минутная стрелки:
| в 3 часа утра | в 20 часов | в 18 часов 30 минут |
|

|

|

|
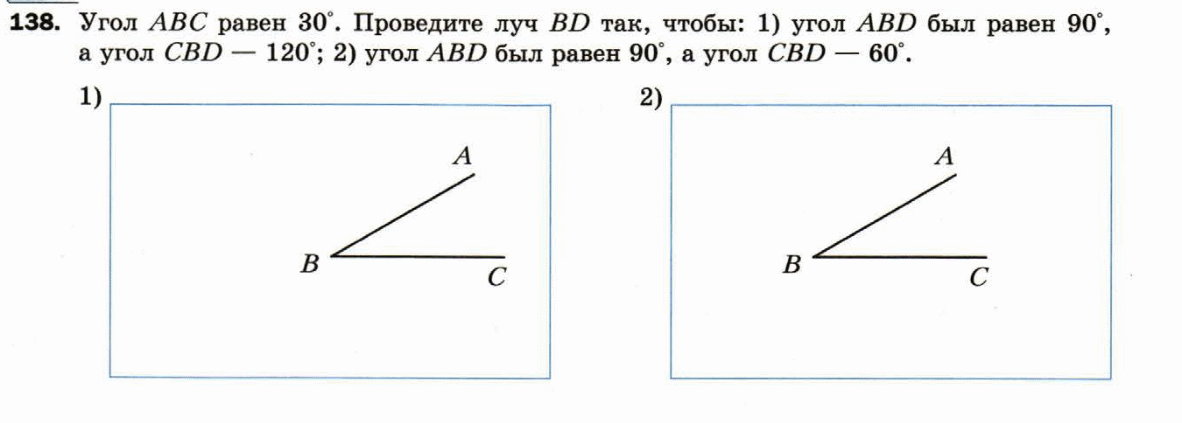
Задание 7.
Угол АВС равен 30°. Проведите луч BD так, чтобы
| угол ABD был равен 90°, а угол CBD равен 120° | угол ABD был равен 90°, а угол CBD равен 60° |
|
|

|
Практическая работа №3
«Построение прямоугольника с заданными сторонами на нелинованной бумаге»
Цели работы:
Познакомиться с алгоритмом построения прямоугольника с заданными сторонами на нелинованной бумаге.
Научиться строить прямоугольник с заданными сторонами на нелинованной бумаге.
Оборудование: чертёжный угольник, линейка, карандаш.
Ход работы
Познакомьтесь с алгоритмом построения прямоугольника с заданными сторонами на нелинованной бумаге.
С помощью угольника чертим прямой угол с вершиной в точке А. | 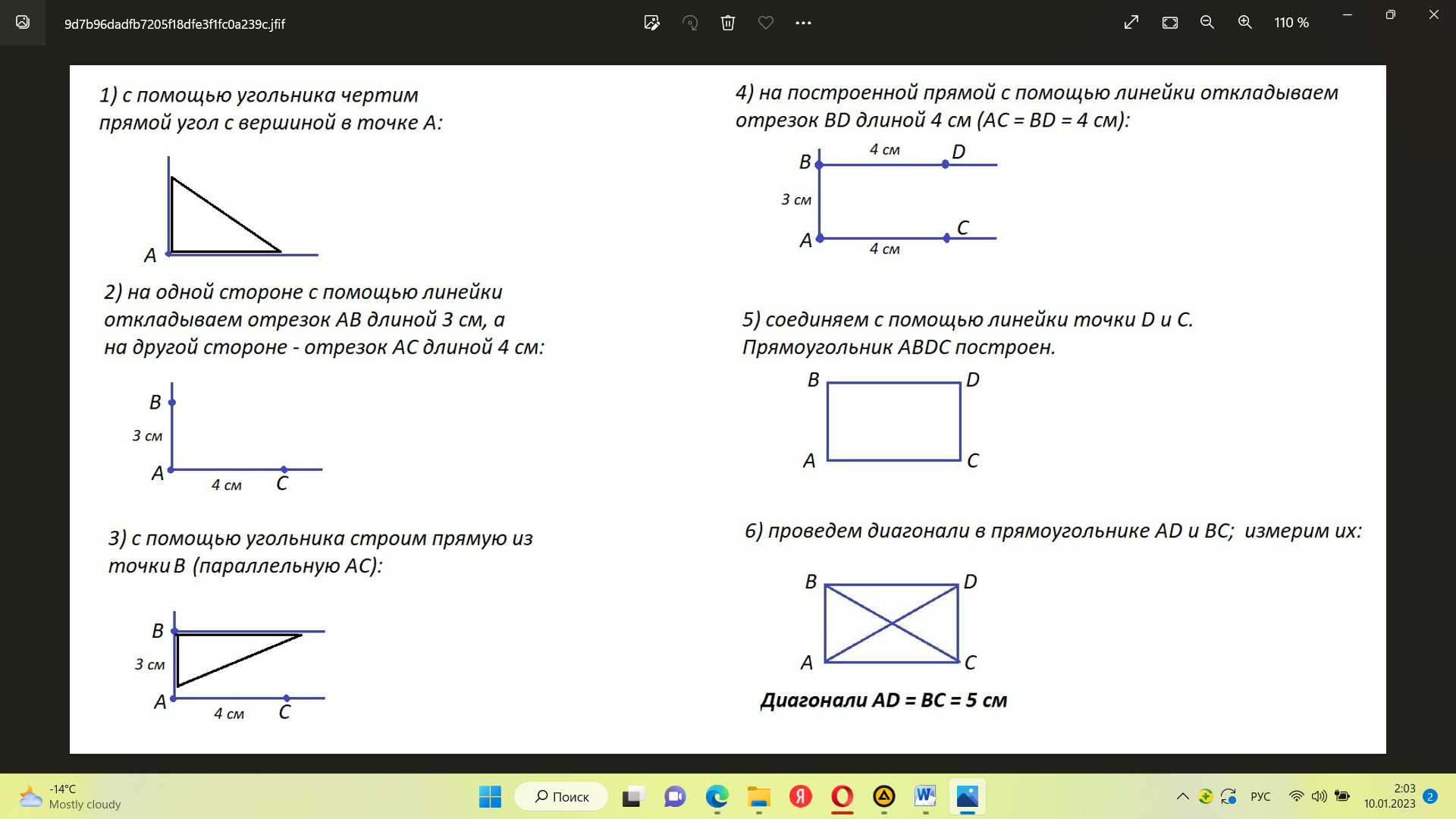
|
На одной стороне с помощью линейки откладываем отрезок АВ длиной 3 см. а на другой стороне – отрезок АС длиной 4 см. | 
|
С помощью угольника строим прямую из точки В (параллельную АС). | 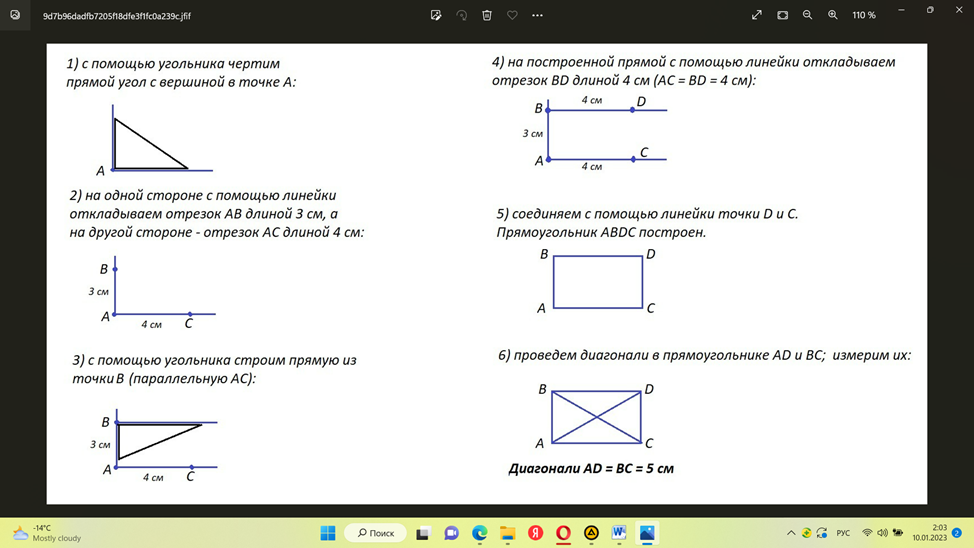
|
На построенной прямой с помощью линейки откладываем отрезок BD длиной 4 см (AC = BD = 4 см). | 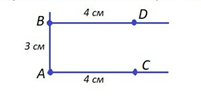
|
Соединяем с помощью линейки точки D и С. Прямоугольник ABCD построен. | 
|
Проведем диагонали AD и BC в прямоугольнике и измерим их. | 
|
| Диагонали AD=BC=5см. |
|
Задание 1.
Выполните построение прямоугольника ABCD с указанными длинами сторон и проведите в нем диагонали, заполните таблицу.
| Длина стороны, a см | Длина стороны, b см | Длина диагонали AD | Длина диагонали BC |
| 4 | 5 |
|
|
Контрольный вопрос:
Сравните длины диагоналей, сделайте вывод, запишите его в тетрадь.
Вычислите периметр и площадь получившегося прямоугольника.
Задание 2.
| Начертите два разных прямоугольника, периметры которых равны периметру данного прямоугольника. Начертите квадрат, периметр которого равен периметру данного прямоугольника | 
|
Заполните таблицу:
| Прямоугольник | Длина | Ширина | Площадь | Периметр |
| 1 |
|
|
|
|
| 2 |
|
|
|
|
| 3 |
|
|
|
|
| 4 |
|
|
|
|
Периметры прямоугольников равны. Равны ли их площади? Какой из прмоугольников имеет наибольшую площадь?
Практическая работа №4 «Куб. Изображение куба»
Цели работы:
Изучить геометрическую объёмную фигуру куб.
Определить сколько граней, рёбер, вершин.
Определить размеры рёбер и углов.
Определить форму граней.
Выяснить, какие предметы окружающего мира имеют форму куба.
Научиться чертить куб.
Оборудование: кубики, линейка
Ход работы.
Рассмотрите внимательно фигуру. Пересчитайте грани куба. Грань куба - это стороны куба. Сколько их? Запишите ответ в тетрадь.
Покажите боковые грани куба. Сколько их. Запишите в тетрадь. Покажите верхнюю грань. Сколько их. Запишите. Покажите нижнюю грань куба. Сколько их. Запишите.
Какой геометрической фигурой является грань куба? Запишите ответ.
Пересчитайте все рёбра куба. Ребро куба – это отрезок, соединяющий 2 грани. Сколько рёбер в кубе? Запишите ответ в тетрадь.
Равны ли рёбра по длине? Запишите в тетрадь.
Верно ли, что каждые две грани имеют общее ребро? Запишите ответ.
Сколько вершин у куба? Вершина куба– это угол куба. Запишите в тетрадь.
Сколько рёбер пересекаются (сходятся) в одной вершине? Запишите в тетрадь.
Какие углы в кубе (острые, прямые, тупые)? Запишите в тетрадь.
Определите, куб - это плоская или объёмная фигура? Объясните. Запишите ответ в тетради.
Научитесь чертить куб в тетради. Выполните действия по порядку:
Чертим квадрат со стороной 2 см. Отмечаем точки – вершины.
От верхней левой вершины проводим диагональ через 2 клетки направо вверх. Отмечаем вершину точкой.
Проводим 2см направо и отмечаем вершину. Соединяем эту вершину с верхним правым углом квадрата. Получилась верхняя грань куба.
От нижнего правого угла квадрата проводим диагональ через 2 клетки направо вверх. Отмечаем вершину. Ведём 2 см вверх и соединяем точки. Получилась боковая грань куба.
Это видимые грани. Сколько их?
Невидимые рёбра проводим пунктирной (прерывистой) линией. Находим нижнюю левую точку первоначального квадрата. От неё проводим диагональ через 2 клетки направо вверх пунктиром. Отмечаем вершину. Ведём пунктир вверх до вершины. Самостоятельно проведите ещё одно невидимое ребро.
Сверьте ответы с образцом и оцените свою работу.
За каждый правильный ответ 1 балл. За правильный чертёж куба 3 балла.
13-15 баллов – оценка «5»
10-12 баллов - оценка «4»
6-9 баллов – оценка «3»
0-5 баллов – оценка «2»
Практическая работа №5 «Площадь поверхности прямоугольного параллелепипеда»
Цели работы:
Познакомиться с алгоритмом измерения длины, ширины и высоты куба и прямоугольного параллелепипеда.
Научиться вычислять площадь поверхности куба и площадь поверхности прямоугольного параллелепипеда.
Оборудование: прямоугольные параллелепипеды, кубики, линейка.
Ход работы
И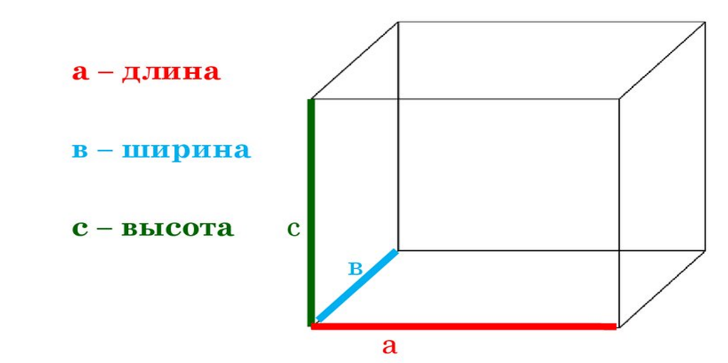 змерьте длину, ширину и высоту прямоугольного параллелепипеда (куба).
змерьте длину, ширину и высоту прямоугольного параллелепипеда (куба).
Вычислите площадь полной поверхности прямоугольного параллелепипеда.
S=2(ab + bc + ac)
Вычислите площадь полной поверхности куба.
S=6a2
Сделайте вычисления.
Перенесите таблицу в тетрадь и заполните её.
| Геометрическая фигура | Длина, a см | Ширина, b см | Высота, c см | Площадь поверхности, S см2 |
| Прямоугольный параллелепипед |
|
|
|
|
| Куб |
|
|
|
|
Контрольные вопросы:
Что можно сказать о противоположных гранях прямоугольного параллелепипеда? Сделайте вывод, запишите его в тетрадь.
Что можно сказать о гранях куба? Сделайте вывод, запишите его в тетрадь.
Дополнительные вопросы и задания:
1. Выразите:
а) в кубических дециметрах: 5 м3 680 см3; 7 м3 15 см3;
б) в кубических сантиметрах: 4 дм3 536 см3; 2 дм3 80 см3.
2. Сколько кубиков с ребром 10 см необходимо взять, чтобы построить башню длиной 25 м, шириной 6 м и высотой 100 м?







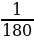 доле развернутого угла.
доле развернутого угла.

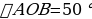
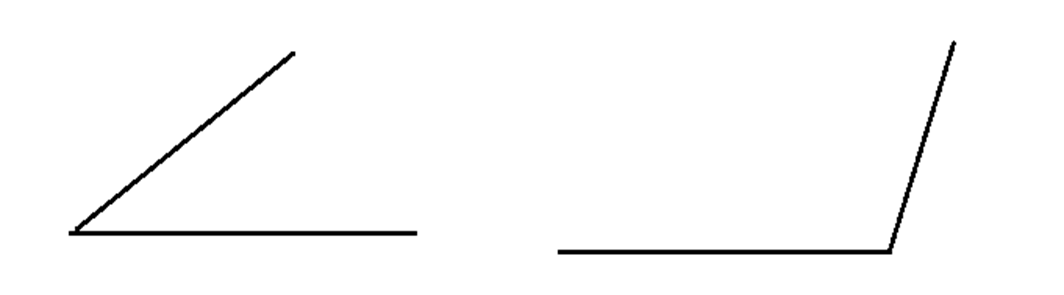
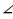 КLM = 75°
КLM = 75° 








 змерьте длину, ширину и высоту прямоугольного параллелепипеда (куба).
змерьте длину, ширину и высоту прямоугольного параллелепипеда (куба).









