ПРАКТИЧЕСКАЯ РАБОТА №28
«Исследование функции и построение ее графика»
ЦЕЛЬ РАБОТЫ:
Корректировать знания, умения и навыки в теме: «Исследование функции и построение ее графика».
Закрепить и систематизировать знания по теме.
Определить уровень усвоения знаний, оценить результат деятельности уч-ся.
ОБОРУДОВАНИЕ: инструкционно-технологические карты, таблицы производных элементарных функций, микрокалькуляторы.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ:
Ответить на контрольные вопросы:
а) Какую точку называют критической (стационарной) точкой функции?
б) Сформулируйте признак возрастания (убывания) функции.
в) Сформулируйте признак максимума (минимума) функции.
г) Опишите схему исследования функции.
С помощью обучающей таблицы повторить план исследования функции и изучить образцы решенных примеров.
Выполнить задания для самоконтроля (в таблице).
Изучить условие заданий для практической работы.
Оформить отчет о работе.
Теория.
1. Схема исследования функции.
Найти область определения функции D(f).
Проверить функцию на четность и нечетность.
Найти f(-x). Если 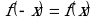 – функция четная;
– функция четная;
Если 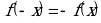 – функция нечетная;
– функция нечетная;
Если  – функция ни четная ни нечетная.
– функция ни четная ни нечетная.
3. Найти точки пересечения графика функции с осями координат.
4. Найти асимптоты графика функции.
5. Найти интервалы возрастания и убывания функции и ее экстремумы.
6. Найти интервалы выпуклости функции и точки перегиба.
7.Построить график, при необходимости найти дополнительные точки.
Экстремумы функции. Промежутки возрастания и убывания.
Определение 7. Функция 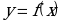 называется возрастающей на промежутке
называется возрастающей на промежутке 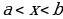 , если для любых
, если для любых 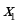 и
и 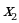 , принадлежащих этому промежутку и таких ,что
, принадлежащих этому промежутку и таких ,что 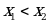 имеет место неравенство
имеет место неравенство 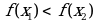 .
.
Определение 8. Функция 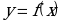 называется убывающей на промежутке
называется убывающей на промежутке 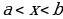 , если для любых
, если для любых 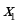 и
и 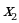 , принадлежащих этому промежутку и таких, что
, принадлежащих этому промежутку и таких, что 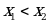 имеет место неравенство
имеет место неравенство 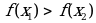 .
.
Как возрастающие, так и убывающие функции называются монотонными, а промежутки, в которых функция возрастает или убывает, - промежутками монотонности.
Возрастание и убывание функции 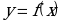 характеризуется знаком ее производной:
характеризуется знаком ее производной:
если производная в некотором промежутке 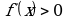 , то функция возрастает;
, то функция возрастает;
если же 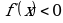 , то функция убывает в этом промежутке.
, то функция убывает в этом промежутке.
Исследование на экстремум функции
Определение 9. Точка  из области определения функции
из области определения функции 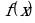 называется точкой минимума этой функции, если существует такая
называется точкой минимума этой функции, если существует такая 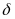 -окрестность
-окрестность 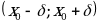 точки
точки 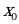 , что для всех ,
, что для всех ,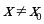 из этой окрестности выполняется неравенство
из этой окрестности выполняется неравенство 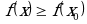
Определение 10. Точка 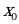 из области определения функции
из области определения функции 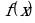 называется точкой максимума этой функции, если существует такая
называется точкой максимума этой функции, если существует такая 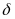 -окрестность
-окрестность 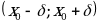 точки
точки 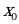 , что для всех ,
, что для всех ,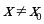 из этой окрестности выполняется неравенство
из этой окрестности выполняется неравенство 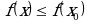 .
.
Точки максимума и минимума называются экстремальными точками (или точками экстремума) данной функции, а значения функции в этих точках - минимумом и максимумом ( или экстремумами) функции.
Точками экстремума могут служить только критические точки, т.е. точки, принадлежащие области определения функции, в которых производная 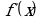 обращается в нуль или терпит разрыв.
обращается в нуль или терпит разрыв.
Если при переходе через критическую точку 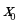 производная
производная 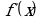 меняет знак, то функция
меняет знак, то функция 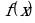 имеет в точке
имеет в точке 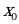 экстремум:
экстремум:
-минимум, когда производная меняет свой знак с минуса на плюс;
-максимум, когда производная меняет свой знак с плюса на минус.
Если же при переходе через критическую точку 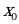 производная
производная 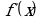 не меняет знака, то функция
не меняет знака, то функция 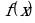 не имеет в точке
не имеет в точке 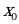 экстремума.
экстремума.
Правило нахождения экстремумов функции 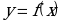 с помощью первой производной.
с помощью первой производной.
Найти производную 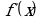 .
.
Найти критические точки функции 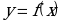 , т.е. точки, в которых
, т.е. точки, в которых 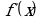 обращается в нуль или терпит разрыв.
обращается в нуль или терпит разрыв.
Исследовать знак производной 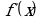 в промежутках, на которые найденные критические точки делят область определения функции
в промежутках, на которые найденные критические точки делят область определения функции 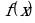 .
.
Вычислить значения функции в точках экстремума.
Пример. Для функции 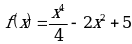 найти промежутки монотонности и точки экстремума функции.
найти промежутки монотонности и точки экстремума функции.
Решение.
Найдем производную функции 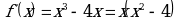 .
.
Найдем критические точки, т.е. решим уравнение 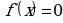 ,
, 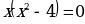 .
.
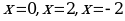
Исследуем знак первой производной 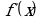 в некоторой окрестности каждой критической точки:
в некоторой окрестности каждой критической точки:
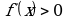 на
на 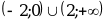 ;
; 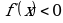 на
на 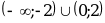 . Следовательно,
. Следовательно, 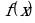 возрастает на
возрастает на 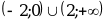 и убывает на
и убывает на 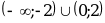 .
.
Точки 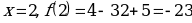 и
и 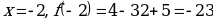 - точки минимума.
- точки минимума.
Точка 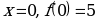 - точка максимума.
- точка максимума.
9. Выпуклость функции. Точки перегиба.
Определение 11. Кривая 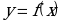 называется выпуклой вниз в промежутке
называется выпуклой вниз в промежутке 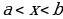 , если она лежит выше любой касательной в любой точке этого промежутка.
, если она лежит выше любой касательной в любой точке этого промежутка.
Определение 12. Кривая 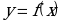 называется выпуклой вверх в промежутке
называется выпуклой вверх в промежутке 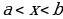 , если она лежит ниже любой касательной в любой точке этого промежутка.
, если она лежит ниже любой касательной в любой точке этого промежутка.
Определение 13. Промежутки, в которых график функции обращен выпуклостью вверх или вниз, называются промежутками выпуклости графика функции.
Выпуклость вверх или вниз кривой, являющейся графиком функции 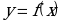 , характеризуется знаком ее второй производной:
, характеризуется знаком ее второй производной:
-если в некотором промежутке 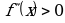 , то кривая выпукла вниз в этом промежутке;
, то кривая выпукла вниз в этом промежутке;
- если в некотором промежутке 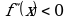 , то кривая выпукла вверх в этом промежутке.
, то кривая выпукла вверх в этом промежутке.
Определение 14. Точка графика функции 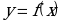 , разделяющая промежутки выпуклости противоположных направлений графика, называется точкой перегиба.
, разделяющая промежутки выпуклости противоположных направлений графика, называется точкой перегиба.
Точками перегиба могут служить только критические точки, принадлежащие области определения функции 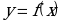 , в которых вторая производная
, в которых вторая производная 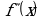 обращается в нуль или терпит разрыв.
обращается в нуль или терпит разрыв.
Если при переходе через критическую точку 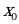 вторая производная
вторая производная 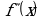 меняет знак, то график функции имеет точку перегиба
меняет знак, то график функции имеет точку перегиба 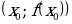 .
.
Правило нахождения точек перегиба графика функции 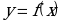 .
.
Найти вторую производную 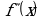 .
.
Найти критические точки функции 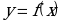 , в которых
, в которых 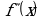 обращается в нуль или терпит разрыв.
обращается в нуль или терпит разрыв.
Исследовать знак второй производной 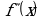 в промежутках, на которые найденные критические точки делят область определения функции
в промежутках, на которые найденные критические точки делят область определения функции 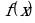 . Если при этом критическая точка
. Если при этом критическая точка 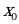 разделяет промежутки выпуклости противоположных направлений, то
разделяет промежутки выпуклости противоположных направлений, то 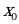 является абсциссой точки перегиба функции.
является абсциссой точки перегиба функции.
Вычислить значения функции в точках перегиба.
Пример. Найти промежутки выпуклости графика функции 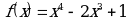 и точки перегиба.
и точки перегиба.
Решение.
Найдем первую и вторую производную:
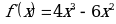 ;
; 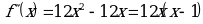 .
.
Найдем критические точки для второй производной:
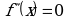 ,
, 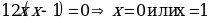 .
.
Выясним знак у 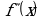 в окрестности каждой точки:
в окрестности каждой точки:
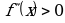 при
при 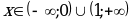 , следовательно график функции на этих промежутках обращен выпуклостью вниз;
, следовательно график функции на этих промежутках обращен выпуклостью вниз;
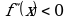 при
при 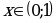 , следовательно график функции на этом промежутке обращен выпуклостью вверх.
, следовательно график функции на этом промежутке обращен выпуклостью вверх.
Абсциссы точек перегиба 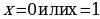 . Найдем значения функции при
. Найдем значения функции при 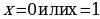 .
.
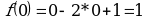 , и
, и 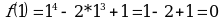
Таким образом, точки перегиба 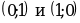 .
.
10. Асимптоты графика функции.
Определение 15. Прямая L называется асимптотой кривой 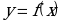 , если расстояние точки M(x;y) кривой от прямой L стремится к нулю при неограниченном удалении этой точки по кривой от начала координат
, если расстояние точки M(x;y) кривой от прямой L стремится к нулю при неограниченном удалении этой точки по кривой от начала координат
(т.е. при стремлении хотя бы одной из координат точки к бесконечности).
Определение 16. Прямая 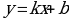 называется наклонной асимптотой кривой
называется наклонной асимптотой кривой 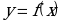 при
при 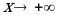 , если
, если
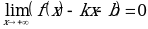
где 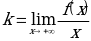 - угловой коэффициент наклонной асимптоты
- угловой коэффициент наклонной асимптоты
и 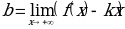 - начальная ордината асимптоты.
- начальная ордината асимптоты.
Аналогично определяется и находится асимптота кривой 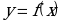 при
при 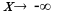 .
.
Определение 17. Асимптота, определяемая уравнением 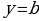 , называется горизонтальной асимптотой.
, называется горизонтальной асимптотой.
Определение 18. Прямая 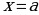 называется вертикальной асимптотой, если
называется вертикальной асимптотой, если 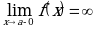 или
или 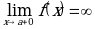 .
.
Для определения вертикальных асимптот надо отыскать те значения х, вблизи которых функция 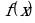 неограниченно возрастает по модулю. Обычно это точки разрыва второго рода данной функции.
неограниченно возрастает по модулю. Обычно это точки разрыва второго рода данной функции.
Пример. Найти асимптоты кривой 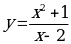 .
.
Решение.Так как 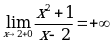 ,
, 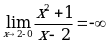 , то прямая
, то прямая 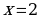 - вертикальная асимптота.
- вертикальная асимптота.
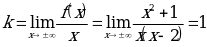 ,
,
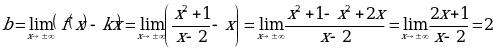 .
.
Итак, прямая 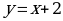 - наклонная асимптота данной функции при
- наклонная асимптота данной функции при 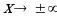 .
.
Таким образом функция имеет вертикальную асимптоту 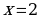 и наклонную асимптоту
и наклонную асимптоту 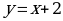 .
.
ОБУЧАЮЩАЯ ТАБЛИЦА
Задание. Исследуйте и постройте графики функции:
а) 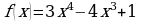 ; б)
; б) 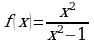 .
.
| № | План исследования | Применение | плана |
| шага | Функции | а) 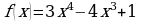 | б) 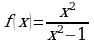 |
| 1 | Находим область определения функции | 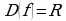
| 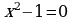 , , 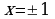 , ,
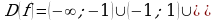
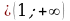
|
| 2 | Исследуем функцию на четность, нечетность | 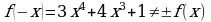 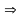 функция ни четная, ни нечетная функция ни четная, ни нечетная
| 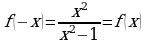 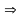 функция четная функция четная
|
| 3 
| Находим нули (корни) функции и промежутки её знакопостоянства | 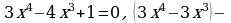 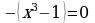 , , 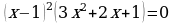 , ,
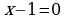 , , 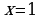 - нуль функции - нуль функции
| 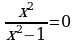 , ,
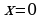 - нуль функции - нуль функции
|
| 4 | Находим производную функции и её критические точки | 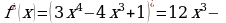 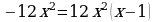 , ,
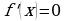 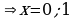 - критические точки функции - критические точки функции
| 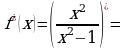
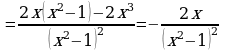 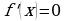 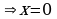 - критическая точка функции - критическая точка функции
|
| 5 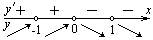
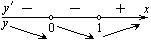
| Находим промежутки монотонности, точки экстремума и экстремумы функции |
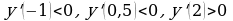
х=0 – не является точкой экстремума, х=1 – точка минимума, 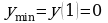 |
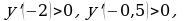
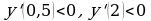 , ,
х=0 – точка максимума, 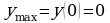
|
| 6 | Находим предел функции при 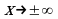 | 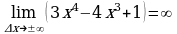
| 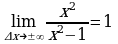
|
| 7 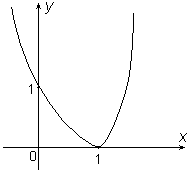
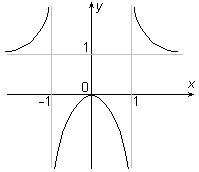
| Строим эскиз графика функции |
|
|
Пример. Построить график функции 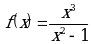 .
.
Область определения функции - вся числовая прямая, кроме 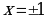 .
.
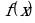 - нечетная функция, так как
- нечетная функция, так как 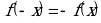 . Поэтому для построения графика функции
. Поэтому для построения графика функции 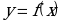 достаточно исследовать ее для
достаточно исследовать ее для 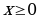 , а затем отобразить симметрично относительно начала координат.
, а затем отобразить симметрично относительно начала координат.
График функции пересекает оси координат только в точке (0;0).
Точки 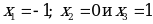 разбивают
разбивают
Так как 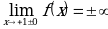 и
и 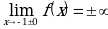 , то прямые
, то прямые 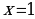 и
и 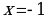 являются вертикальными асимптотами. А так как
являются вертикальными асимптотами. А так как 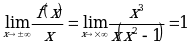 ,
,
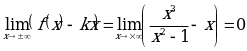 , то график данной функции имеет асимптоту
, то график данной функции имеет асимптоту 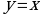 .
.
Найдем производную:
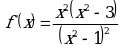 . Она существует во всех точках числовой прямой, кроме
. Она существует во всех точках числовой прямой, кроме 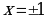 и равна нулю в точках
и равна нулю в точках 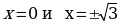 .
.
Поэтому критическими точками функции будут:
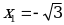 числовую прямую на четыре интервала:
числовую прямую на четыре интервала: 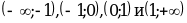 .
.
, 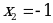 ,
, 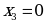 ,
, 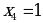 ,
, 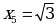 .
.
Изучим поведение 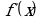 в окрестности каждой критической точки. Вследствие нечетности
в окрестности каждой критической точки. Вследствие нечетности 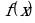 достаточно рассмотреть знак
достаточно рассмотреть знак 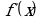 на промежутках
на промежутках 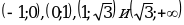 . Результаты исследования запишем в таблицу:
. Результаты исследования запишем в таблицу:
| x | 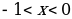
| 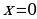
| 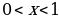
| 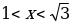
| 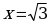
| 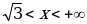
|
| 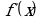
| – | 0 | – | – | 0 | + |
| 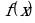
| 
| нет экстремума | 
| 
| минимум =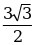 | 
|
В точках 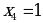 и
и 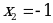 функция не имеет экстремума, так как эти точки не принадлежат области определения данной функции.
функция не имеет экстремума, так как эти точки не принадлежат области определения данной функции.
В силу нечетности функции можно утверждать, что при 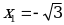 данная функция имеет максимум.
данная функция имеет максимум.
6) Чтобы исследовать график функции на выпуклость, найдем вторую производную:
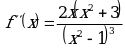 и критические точки данной функции (по второй производной):
и критические точки данной функции (по второй производной): 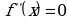 при
при 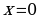 и
и 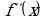 не существует при
не существует при 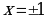 . Однако точки
. Однако точки 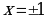 не принадлежат области определения функции, поэтому точа перегиба может быть только в точке с абсциссой
не принадлежат области определения функции, поэтому точа перегиба может быть только в точке с абсциссой 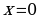 .
.
Исследуем знак второй производной и результаты исследования запишем в таблицу:
| x | 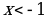
| 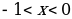
| 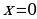
| 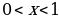
| 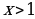
|
| 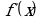
| – | + | 0 | – | + |
| 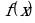
| 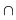
| 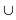
| точка перегиба | 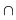
| 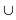
|
На основе проведенного исследования построим график функции.
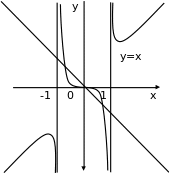
Примеры. Исследуйте и постройте графики функций:
1) 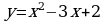 ; 2)
; 2) 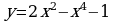 ; 3)
; 3) 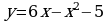 ; 4)
; 4) 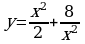 ; 5)
; 5) 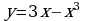 ; 6)
; 6) 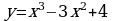 ; 7)
; 7) 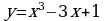 ; 8)
; 8) 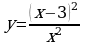 ; 9)
; 9) 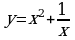 .
.
Задания для самостоятельного решения:
Исследуйте функцию 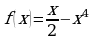 на максимум и минимум.
на максимум и минимум.
Исследуйте с помощью производной функцию 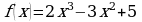 и постройте ее график.
и постройте ее график.
Контрольные вопросы:
1. Сформулируйте определение возрастающей и убывающей функции.
2.Чем можно охарактеризовать возрастание и убывание функции?
Поясните в каком случае функция возрастающая, а в каком убывающая.
3.Определите какие точки называются точками экстремума, (точки максимума и точки минимума).
4.Перечислите этапы нахождения промежутков монотонности и точек экстремума.
5.Дайте определение кривых выпуклых вверх и вниз.
6.Сформулируйте правило нахождения промежутков выпуклости графика функции.
7.Какие точки называются точками перегиба. Сформулируйте правило нахождения точек перегиба.
8. Что такое асимптота?
9. Каких видов бывают асимптоты?
10.Сформулируйте определение наклонной асимптоты.
11. Что такое вертикальная асимптота?
12.Дайте определение горизонтальной асимптоты.
1.Перечислите этапы исследования функции.
18.Как проверить функцию на четность или нечетность.
ВАРИАНТЫ ПРАКТИЧЕСКОЙ РАБОТЫ.
Вариант 1.
Исследуйте функцию 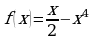 на возрастание и убывание функции и точки экстремума.
на возрастание и убывание функции и точки экстремума.
Составить уравнение касательной и нормали к графику функции в точке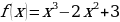 ,
, 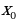 =-1
=-1
Точка движется прямолинейно по закону 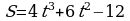 . Найти значение скорости и ускорения в момент времени 2c. Кинетическую энергию, если масса тела равна 4 кг.
. Найти значение скорости и ускорения в момент времени 2c. Кинетическую энергию, если масса тела равна 4 кг.
Найти тангенс угла наклона касательной к графику функции 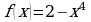 в точке
в точке 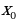 =-1
=-1
5.Исследовать на выпуклость и точки перегиба функции: 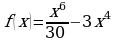
Вариант 2.
Исследуйте функцию 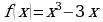 на возрастание и убывание функции и точки экстремума.
на возрастание и убывание функции и точки экстремума.
Найти тангенс угла наклона касательной к графику функции 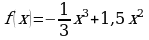 в точке
в точке 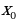 =-3
=-3
Составить уравнение касательной и нормали к графику функции в точке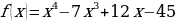 ,
, 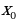 =2
=2
Точка движется прямолинейно по закону 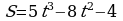 . Найти значение скорости и ускорения в момент времени
. Найти значение скорости и ускорения в момент времени 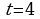 c. Кинетическую энергию, если масса тела равна 3 кг.
c. Кинетическую энергию, если масса тела равна 3 кг.
Исследовать на выпуклость и точки перегиба функцию: 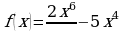
Вариант 3.
Исследуйте функцию 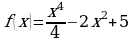 на максимум и минимум.
на максимум и минимум.
Исследуйте на выпуклость и точки перегиба функцию 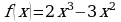
Составить уравнение касательной и нормали к графику функции в точке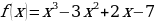 ,
, 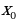 =3
=3
Точка движется прямолинейно по закону 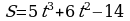 . Найти значение скорости и ускорения в момент времени
. Найти значение скорости и ускорения в момент времени 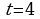 c. Кинетическую энергию, если масса тела равна 5 кг.
c. Кинетическую энергию, если масса тела равна 5 кг.
Найти тангенс угла наклона 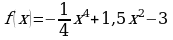 в точке
в точке 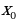 =-1
=-1
Вариант 4.
Исследуйте функцию 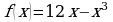 на максимум и минимум.
на максимум и минимум.
Исследуйте на выпуклость и точки перегиба функцию 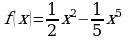
Составить уравнение касательной и нормали к графику функции в точке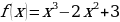 ,
, 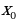 =-1
=-1
Точка движется прямолинейно по закону 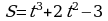 . Найти значение скорости и ускорения в момент времени
. Найти значение скорости и ускорения в момент времени 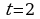 c. Кинетическую энергию, если масса тела равна 3 кг.
c. Кинетическую энергию, если масса тела равна 3 кг.
Найти тангенс угла наклона 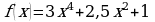 в точке
в точке 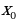 =3
=3
Вариант 5.
Исследуйте функцию 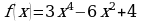 на максимум и минимум.
на максимум и минимум.
Исследуйте на выпуклость и точки перегиба функцию 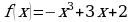 .
.
Составить уравнение касательной и уравнение нормали к кривой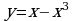 , в точке
, в точке 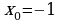 .
.
Точка движется прямолинейно по закону 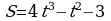 . Найти значение скорости и ускорения в момент времени
. Найти значение скорости и ускорения в момент времени 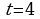 c. Кинетическую энергию, если масса тела равна 5 кг.
c. Кинетическую энергию, если масса тела равна 5 кг.
Найти тангенс угла наклона касательной к графику функции 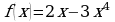 в точке
в точке 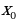 =-1
=-1
Вариант 6.
Исследуйте функцию 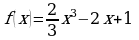 на максимум и минимум.
на максимум и минимум.
Исследуйте на выпуклость и точки перегиба функцию 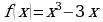 .
.
Составить уравнение касательной и уравнение нормали к кривой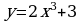 , в точке
, в точке 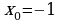 .
.
Точка движется прямолинейно по закону 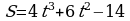 . Найти значение скорости и ускорения в момент времени
. Найти значение скорости и ускорения в момент времени 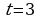 c. Кинетическую энергию, если масса тела равна 4 кг.
c. Кинетическую энергию, если масса тела равна 4 кг.
Найти тангенс угла наклона касательной к графику функции 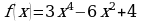 в точке
в точке 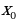 =-1
=-1
Вариант 7.
Исследуйте функцию 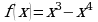 на максимум и минимум.
на максимум и минимум.
Исследуйте на выпуклость и точки перегиба функцию 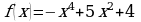 .
.
Составить уравнение касательной и уравнение нормали к кривой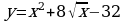 , в точке
, в точке 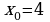 .
.
Точка движется прямолинейно по закону 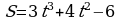 . Найти значение скорости и ускорения в момент времени
. Найти значение скорости и ускорения в момент времени 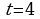 c. Кинетическую энергию, если масса тела равна 2 кг.
c. Кинетическую энергию, если масса тела равна 2 кг.
Найти тангенс угла наклона касательной к графику функции 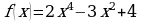 в точке
в точке 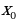 =-1
=-1
Вариант 8.
Исследуйте функцию 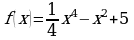 на максимум и минимум.
на максимум и минимум.
Исследуйте на выпуклость и точки перегиба функцию 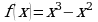
Составить уравнение касательной и уравнение нормали к кривой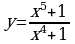 , в точке
, в точке 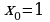 .
.
Точка движется прямолинейно по закону 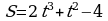 . Найти значение скорости и ускорения в момент времени
. Найти значение скорости и ускорения в момент времени 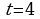 c. Кинетическую энергию, если масса тела равна 4 кг.
c. Кинетическую энергию, если масса тела равна 4 кг.
Найти тангенс угла наклона касательной к графику функции 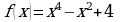 в точке
в точке 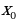 =-1
=-1





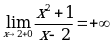 ,
, 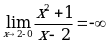 , то прямая
, то прямая 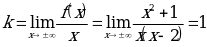 ,
,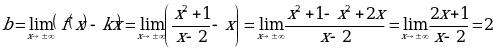 .
.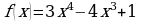 ; б)
; б) 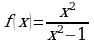 .
.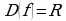
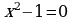 ,
, 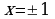 ,
, 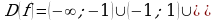
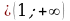
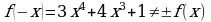
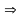 функция ни четная, ни нечетная
функция ни четная, ни нечетная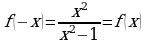
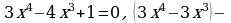
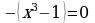 ,
, 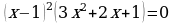 ,
,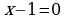 ,
, 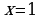 - нуль функции
- нуль функции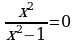 ,
,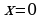 - нуль функции
- нуль функции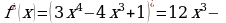
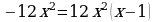 ,
,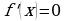
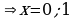 - критические точки функции
- критические точки функции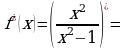
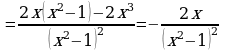
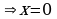 - критическая точка функции
- критическая точка функции

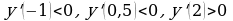
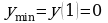
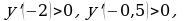
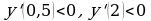 ,
,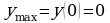
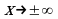
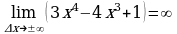
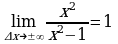


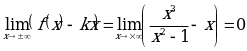 , то график данной функции имеет асимптоту
, то график данной функции имеет асимптоту 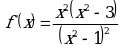 . Она существует во всех точках числовой прямой, кроме
. Она существует во всех точках числовой прямой, кроме 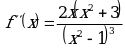 и критические точки данной функции (по второй производной):
и критические точки данной функции (по второй производной): 
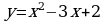 ; 2)
; 2) 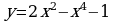 ; 3)
; 3) 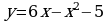 ; 4)
; 4) 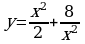 ; 5)
; 5) 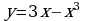 ; 6)
; 6) 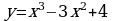 ; 7)
; 7) 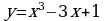 ; 8)
; 8) 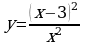 ; 9)
; 9) 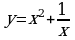 .
.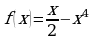 на максимум и минимум.
на максимум и минимум.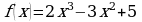 и постройте ее график.
и постройте ее график.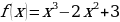 ,
, 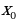 =-1
=-1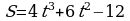 . Найти значение скорости и ускорения в момент времени 2c. Кинетическую энергию, если масса тела равна 4 кг.
. Найти значение скорости и ускорения в момент времени 2c. Кинетическую энергию, если масса тела равна 4 кг. 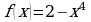 в точке
в точке 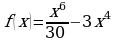
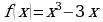 на возрастание и убывание функции и точки экстремума.
на возрастание и убывание функции и точки экстремума.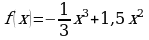 в точке
в точке 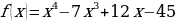 ,
, 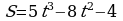 . Найти значение скорости и ускорения в момент времени
. Найти значение скорости и ускорения в момент времени 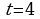 c. Кинетическую энергию, если масса тела равна 3 кг.
c. Кинетическую энергию, если масса тела равна 3 кг. 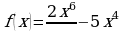
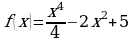 на максимум и минимум.
на максимум и минимум.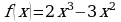
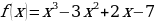 ,
, 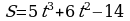 . Найти значение скорости и ускорения в момент времени
. Найти значение скорости и ускорения в момент времени 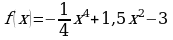 в точке
в точке 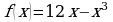 на максимум и минимум.
на максимум и минимум.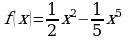
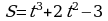 . Найти значение скорости и ускорения в момент времени
. Найти значение скорости и ускорения в момент времени 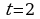 c. Кинетическую энергию, если масса тела равна 3 кг.
c. Кинетическую энергию, если масса тела равна 3 кг. 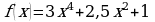 в точке
в точке 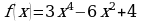 на максимум и минимум.
на максимум и минимум.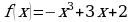 .
.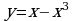 , в точке
, в точке 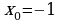 .
.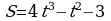 . Найти значение скорости и ускорения в момент времени
. Найти значение скорости и ускорения в момент времени 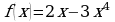 в точке
в точке 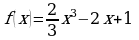 на максимум и минимум.
на максимум и минимум.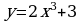 , в точке
, в точке 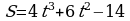 . Найти значение скорости и ускорения в момент времени
. Найти значение скорости и ускорения в момент времени 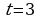 c. Кинетическую энергию, если масса тела равна 4 кг.
c. Кинетическую энергию, если масса тела равна 4 кг. 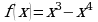 на максимум и минимум.
на максимум и минимум.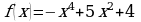 .
.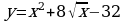 , в точке
, в точке 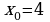 .
.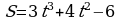 . Найти значение скорости и ускорения в момент времени
. Найти значение скорости и ускорения в момент времени 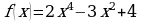 в точке
в точке 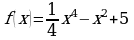 на максимум и минимум.
на максимум и минимум.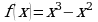
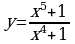 , в точке
, в точке 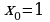 .
.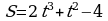 . Найти значение скорости и ускорения в момент времени
. Найти значение скорости и ускорения в момент времени 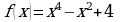 в точке
в точке 









