

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до 24.06.2025
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока

Была в сети 21.07.2022 21:34

Капиева Арзу Яверовна
преподаватель информатики и икт, экономики
42 года
Местоположение
Россия, Южно Сухокумск
Практическая работа "Работа с редактором формул"
Категория:
Информатика
19.07.2022 22:33


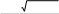 1,2 b b2 4ac
1,2 b b2 4ac 1,2 5 25 24 5 7 , x1 1, x2 2;
1,2 5 25 24 5 7 , x1 1, x2 2; 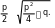
 апример, корни уравнения x2 6x70 таковы: x1,2 3 9 7 3 4, x1 7, x2 1.
апример, корни уравнения x2 6x70 таковы: x1,2 3 9 7 3 4, x1 7, x2 1.


















