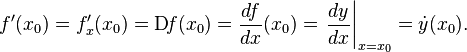Практическое занятие
Тема: «Математический анализ».
Наименование работы: «Вычисление производных функций».
Цель: совершенствовать умения вычислять производные функций.
Содержание
Часть 1. Теоретическая
Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке).
Процесс вычисления производной называется дифференци́рованием. Обратный процесс — нахождение первообразной — интегрирование.
Иллюстрация понятия производной
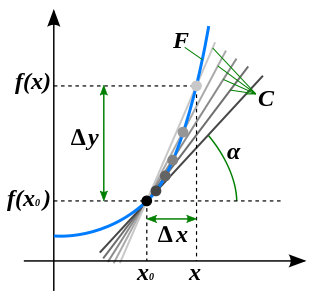
Определение производной функции через предел
Пусть в некоторой окрестности точки 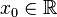 определена функция
определена функция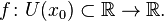 Производной функции
Производной функции 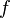 в точке
в точке 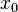 называется предел, если он существует,
называется предел, если он существует,
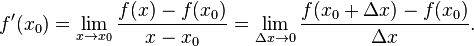
Общепринятые обозначения производной функции
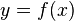
в точке
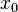
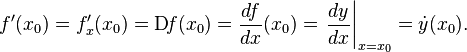
Заметим, что последнее обычно обозначает производную по времени (в теоретической механике).
Таблица производных
| Производные степенных функций | Производные тригонометрических функций | Производные обратных тригонометрических функций |
| 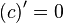
| 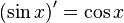
| 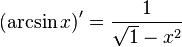
|
| 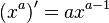
| 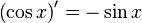
| 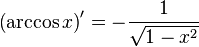
|
| 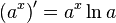
| 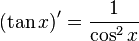
| 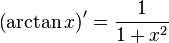
|
| 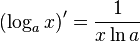
| 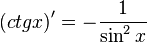
| 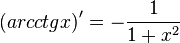
|
Правила дифференцирования
Операция нахождения производной называется дифференцированием. При выполнении этой операции часто приходится работать с частными, суммами, произведениями функций, а также с «функциями функций», то есть сложными функциями. Исходя из определения производной, можно вывести правила дифференцирования, облегчающие эту работу. Если C — постоянное число и f=f(x), g=g(x) — некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:
Пример: Найти производную функции .
Решение. .
Пример: Найти производную функции  и вычислить ее значения в точках
и вычислить ее значения в точках  и
и 
Решение.
Пример: Найти производную функции .
Решение.
Пример: Найти производную функции .
Решение.
Часть 2. Практическая
Задание: Вычислите производные следующих функций:
| № | Задание | № | Задание |
| 1 | а) у = , б) у= , б) у= , , в) у= г) y = г) y =  | 6 | а) у=  , б) у= , б) у= , в) г) y = ln(1 + cosx) , в) г) y = ln(1 + cosx) |
| 2 | а) у=  б) у= б) у= , , в)  , г) y = , г) y =  | 7 | а) у= б) у= , в) у= , в) у= , г) y = 2sin5x – cos2x , г) y = 2sin5x – cos2x |
| 3 | а) у =  б) у= б) у= в)  г) y = г) y =  | 8 | а) у= б) у= , в) , в)  , г) y = tg( , г) y = tg( ) ) |
| 4 | а) у =  , б) у= , б) у= , в) в) , в) в)  , г) y = , г) y =  | 9 | а) у=  , б) у= , б) у= , , в)  г) y = lntg5x г) y = lntg5x |
| 5 | а) у =  , б) у= , б) у= , в) у= , в) у= , г) y = lnsinx , г) y = lnsinx | 10 | а) у=  б) у= б) у= , в) , в)  , г) y= , г) y=  |
Вопросы к практическому занятию
-
Дайте определение производной.
-
Как называется действие нахождение производной?
-
Запишите формулу производной суммы.
-
Запишите формулу производной произведения.
-
Запишите формулу производной частного.
-
Чему равна производная константы.
-
Выучите формулы производных элементарных функций.
-
Как вычислить производную сложной функции?