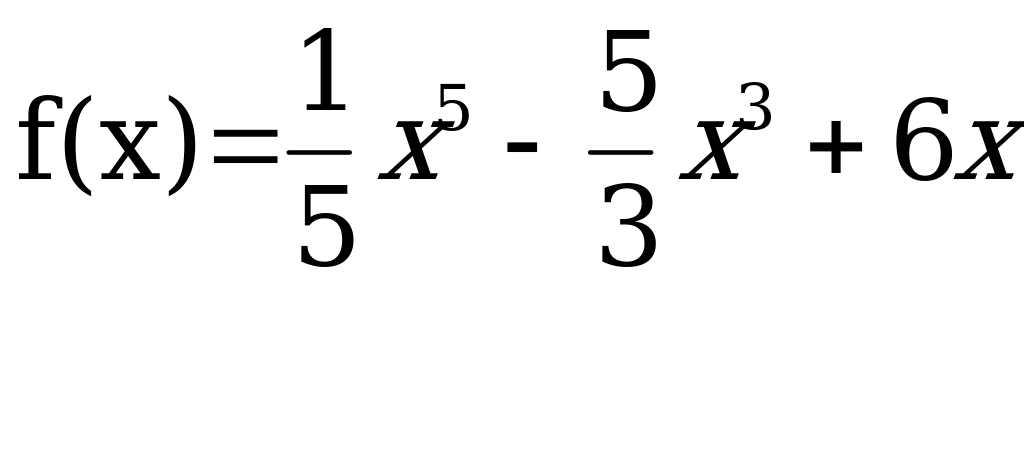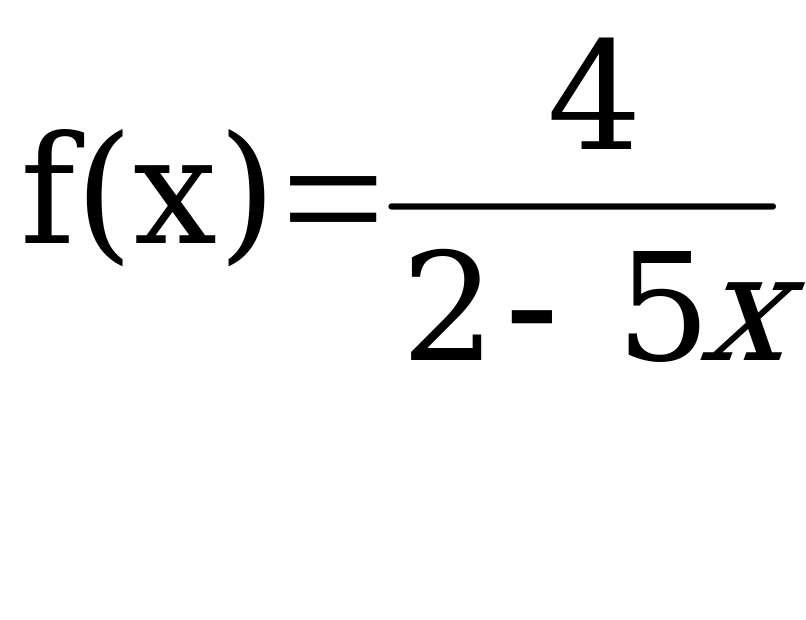Задание по математике за 2 семестр
для группы заочного отделения
ЮРЗ-22-09
1 Общие методические указания к выполнению работы
Задание по дисциплине «Математика» предполагает решение набора типовых задач по нескольким темам учебной программы.
Отчёт по выполненной работе представляет собой набор решённых задач с необходимыми пояснениями и расчётами.
2. К сессии допускаются студенты, выполнившие задание (можно не решать все примеры, если они кажутся однотипными, но аналогичные примеры будут на экзамене!!!)
3. Задание выполняется на листах формата А 4(задание может быть написано «от руки» (так, чтобы его можно было прочитать) или напечатано) или в отдельной тетради в клетку чернилами синего, черного или фиолетового цвета
4. На титульном листе указать название дисциплины, номер группы и ФИО студента.
5. Задание второго семестра состоит из трех тем:
1) тригонометрические функции, тригонометрические уравнения;
2) производная функции, использование производной для исследования функции;
3) многогранники и тела вращения, площади поверхностей и объемы.
6. Каждая новая тема начинается с новой страницы. Условие задачи приводить обязательно.
7. Выполненные задания должны содержать все необходимые пояснения, формулы и расчеты.
2 Задания 2.1 Тригонометрические функции, тригонометрические уравнения
Справочный материал
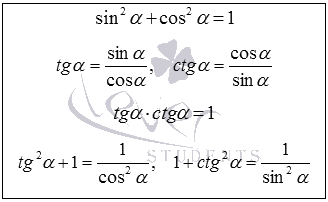
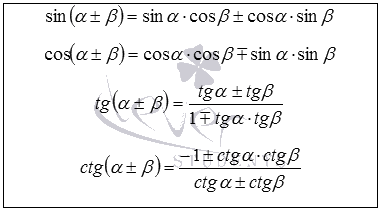
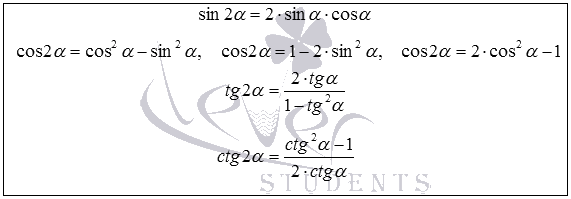
Вычислить:
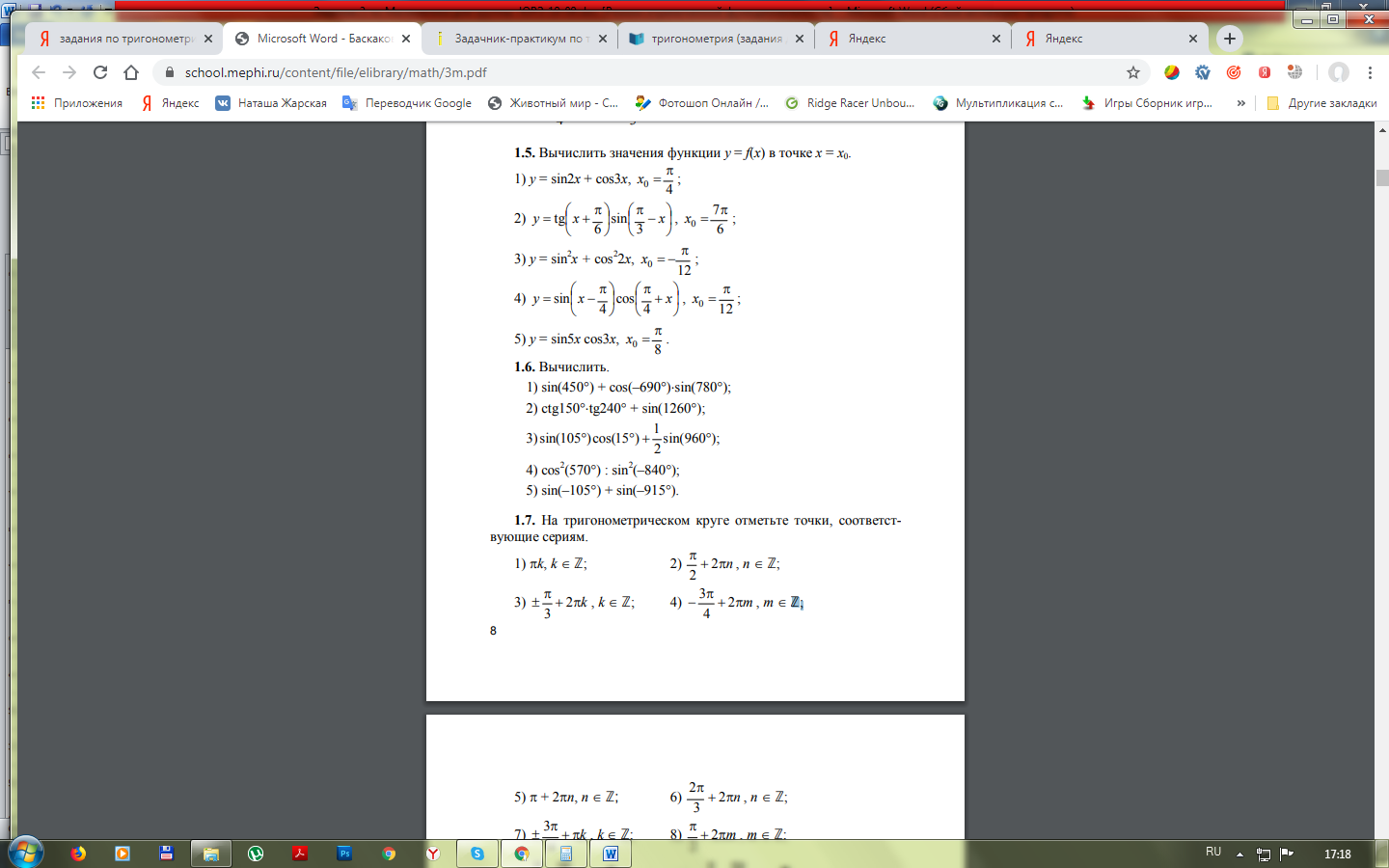
Вычислить:
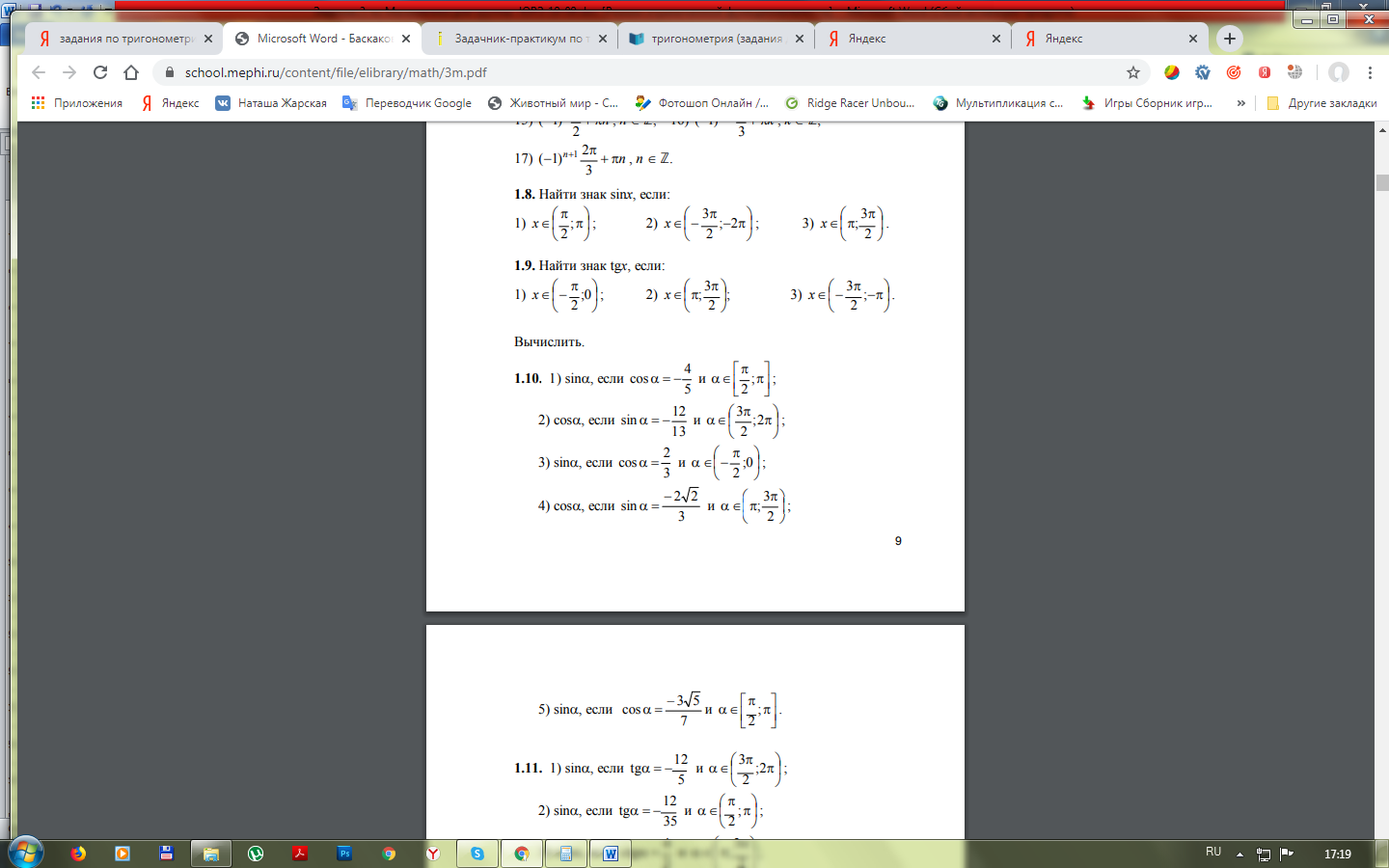
Вычислить:
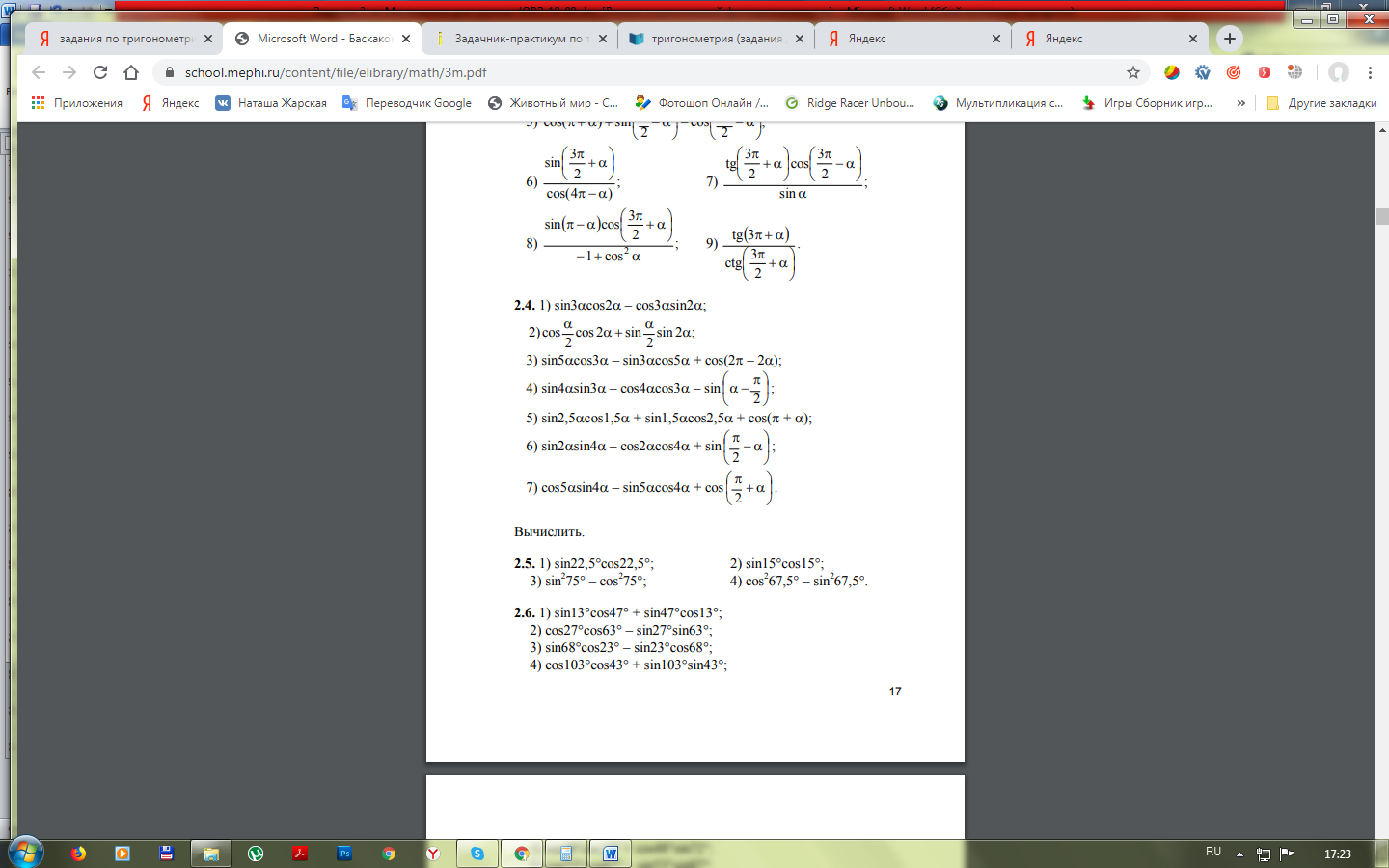
Вычислить:
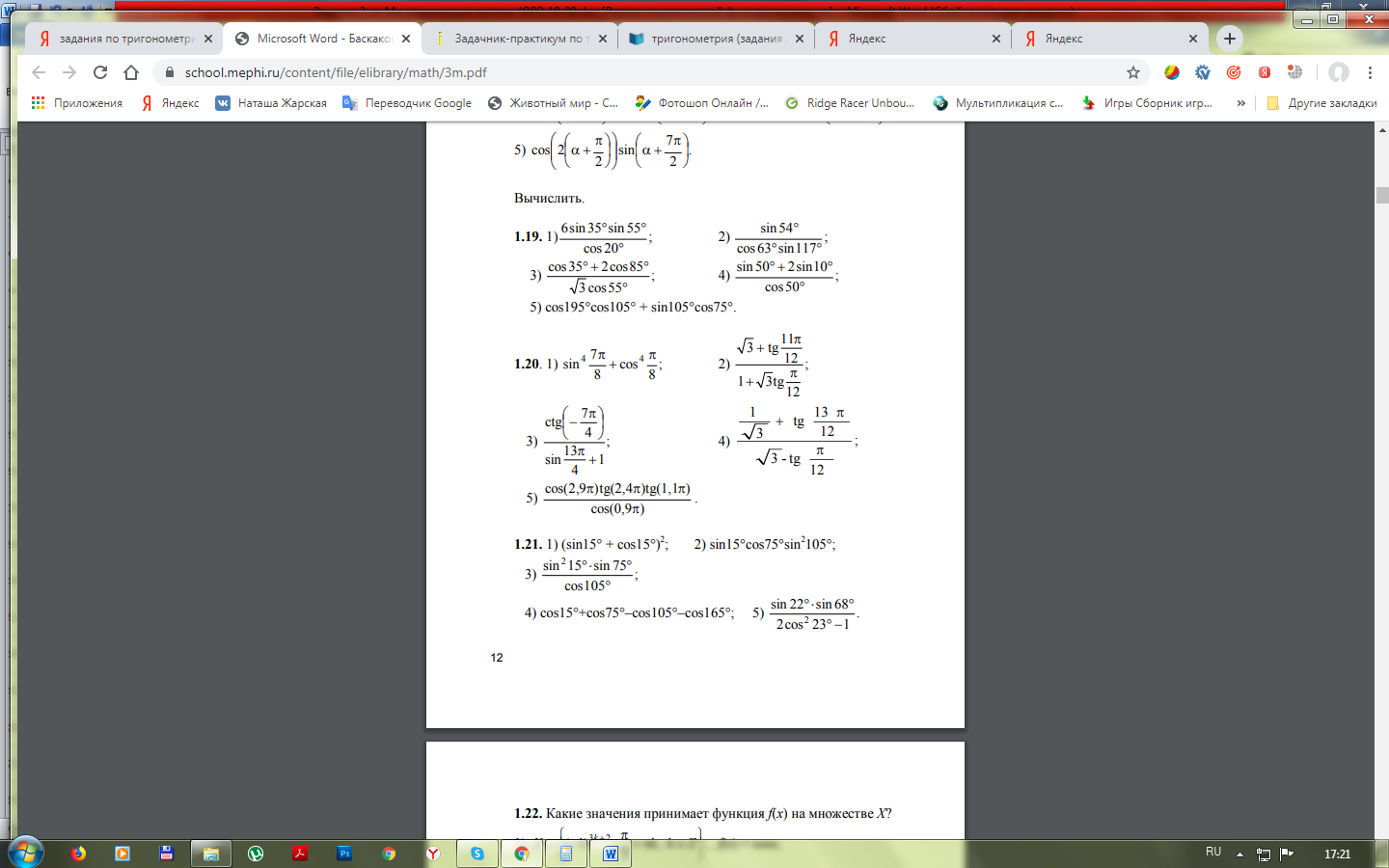
Упростить выражение:
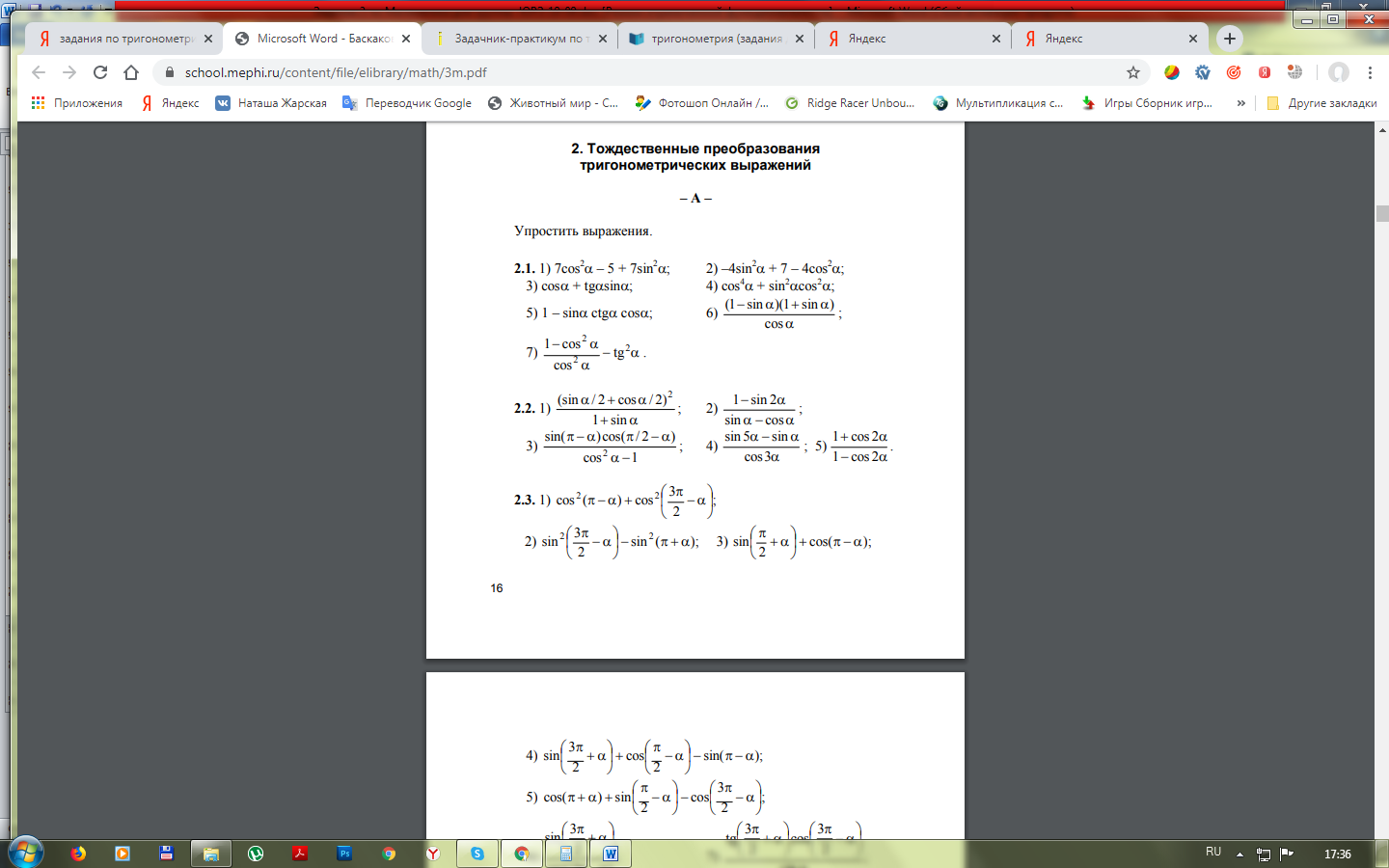
Решить уравнения
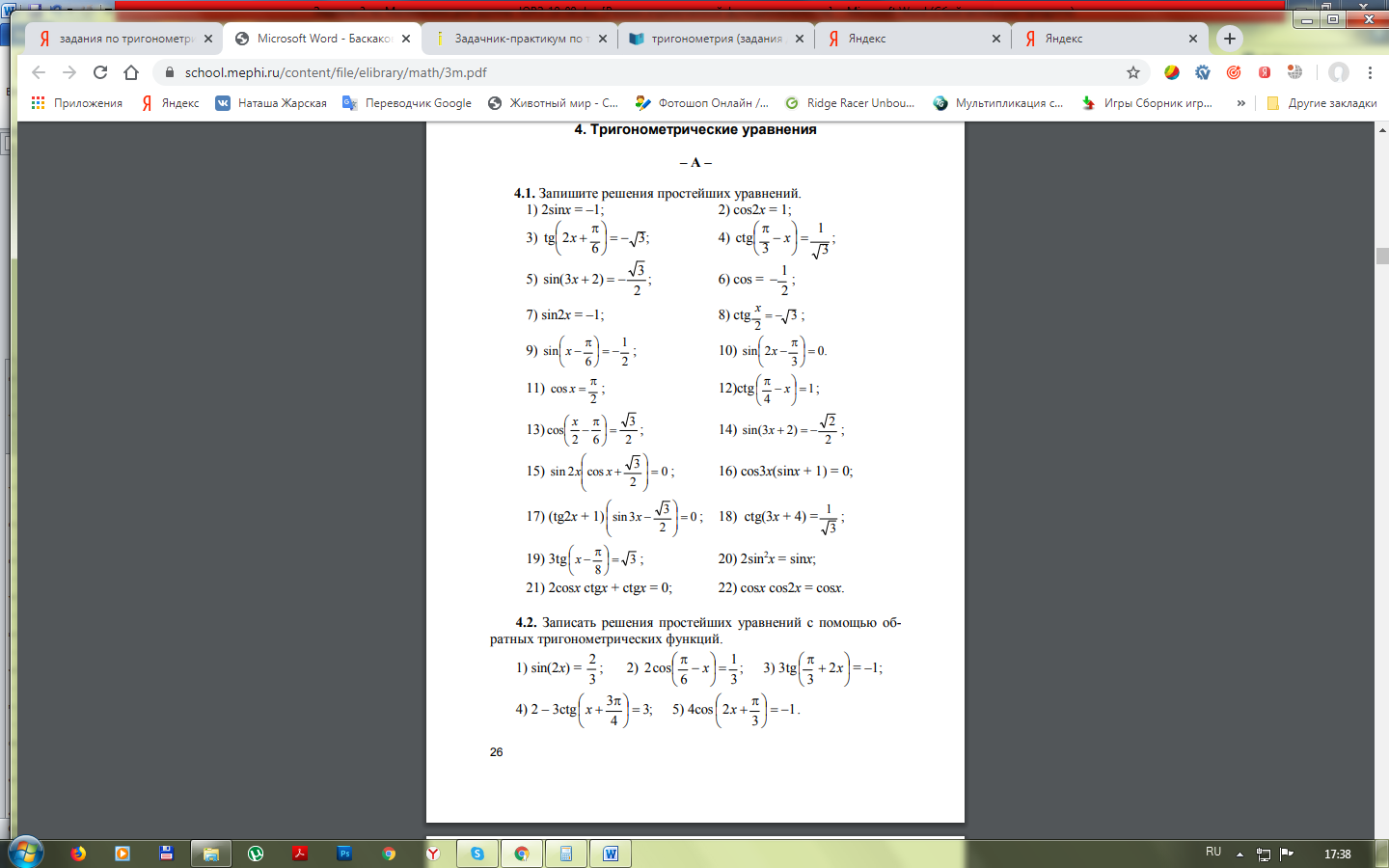
! ( в 6-ом уравнении cosх)
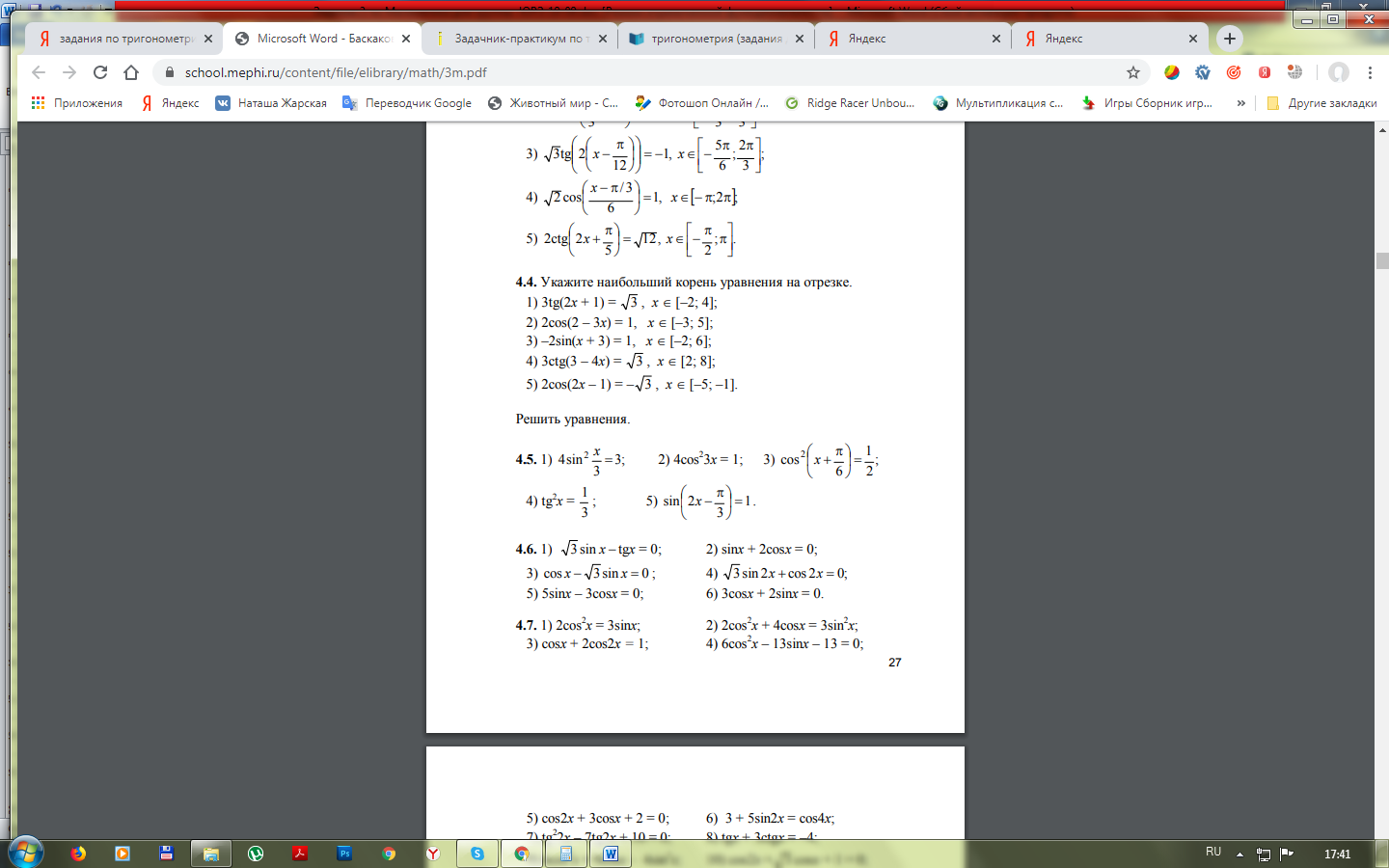
Уравнения, приводимые к квадратным:
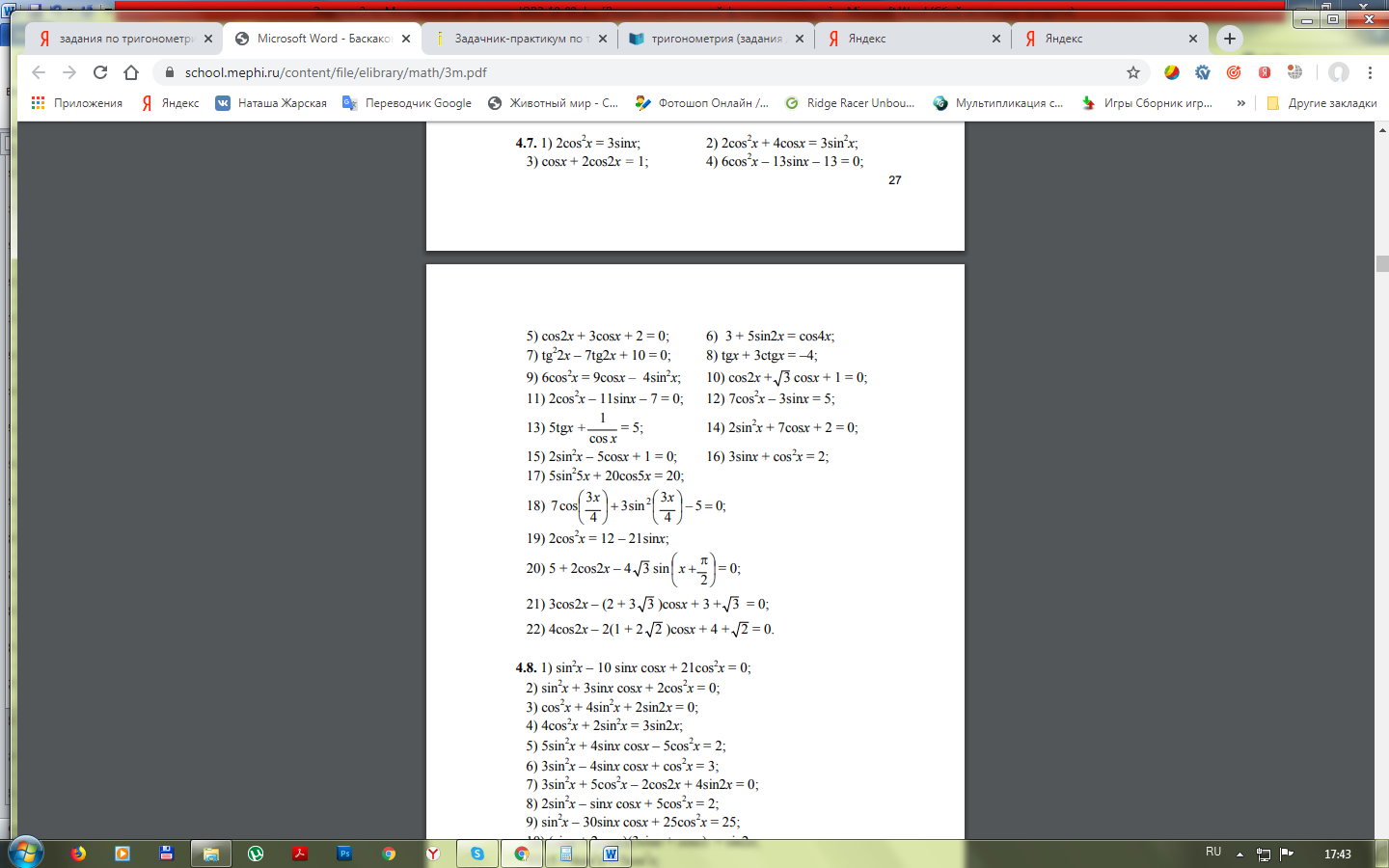
Однородные уравнения второй степени:

2.2 Производная функции,
использование производной для исследования функции
Справочный материал
Таблица производных
Если имеется дифференцируемая функция U(x), то справедливы формулы:
1. 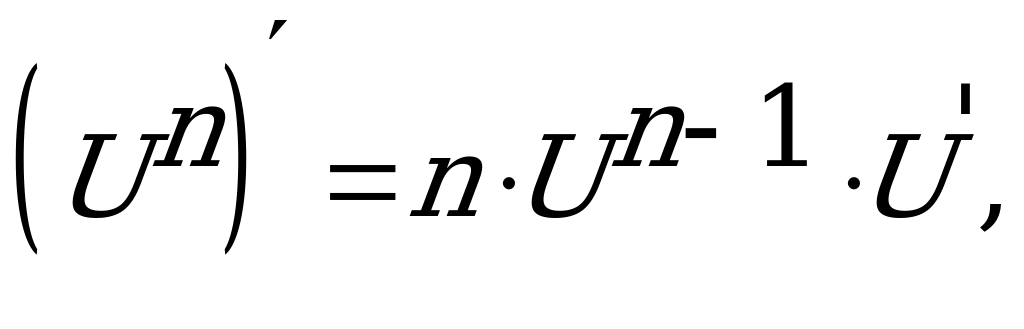 где n – любое действительное число.
где n – любое действительное число.
2. 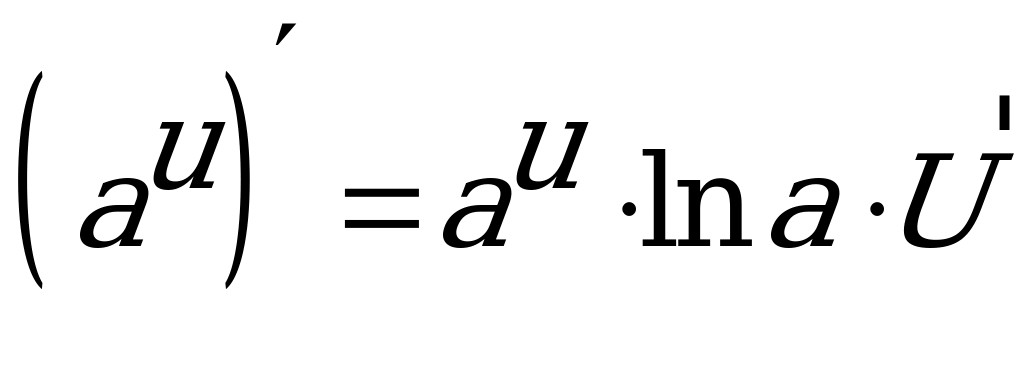 , где a0, a – действительное число.
, где a0, a – действительное число.
3. 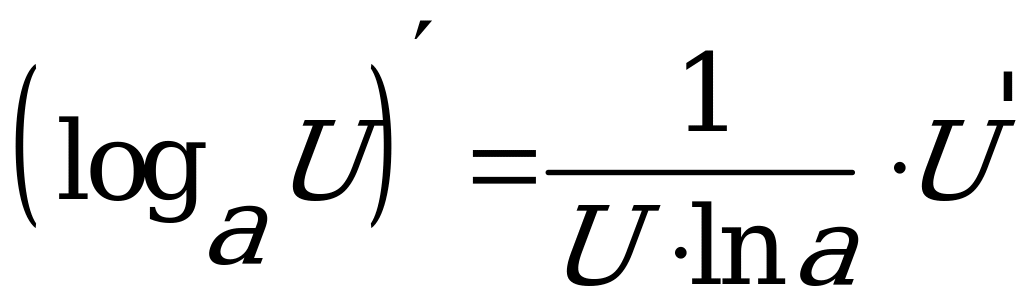 .
.
4. 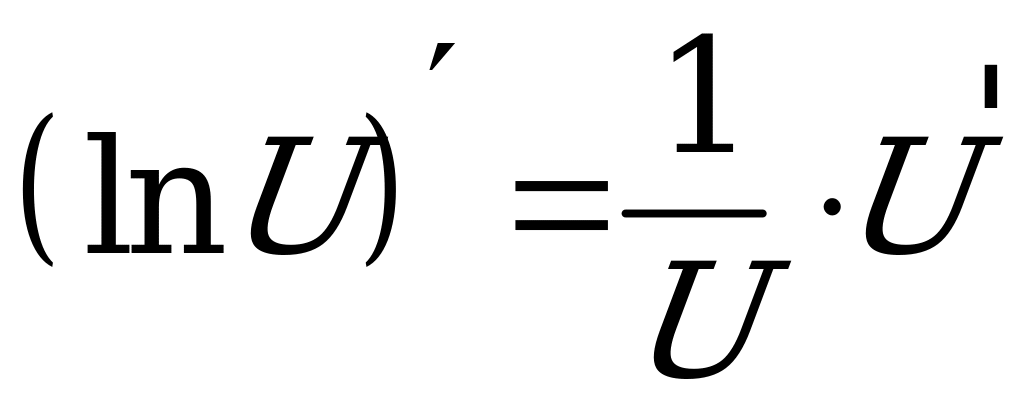 .
.
5. 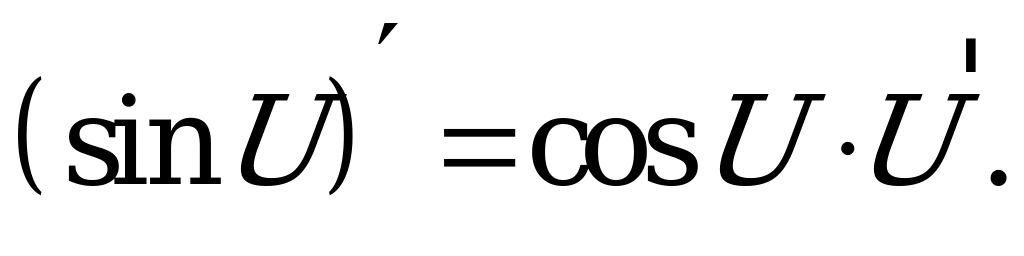
6. 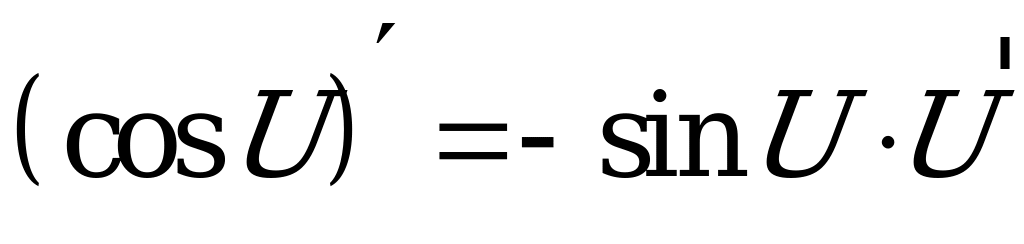 .
.
7. 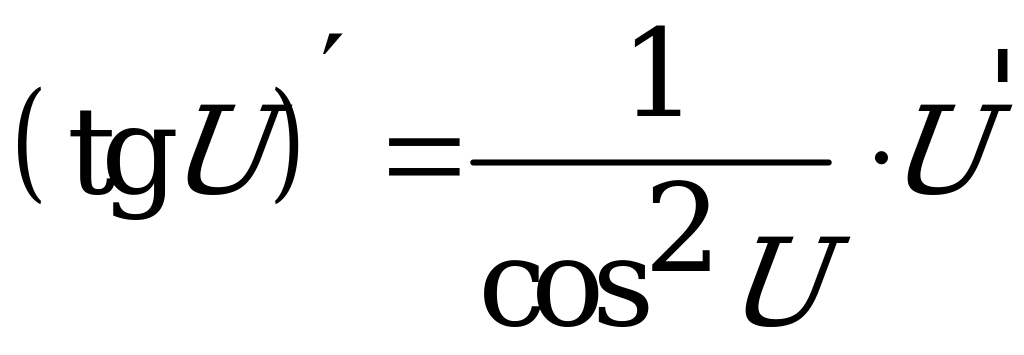 .
.
8. 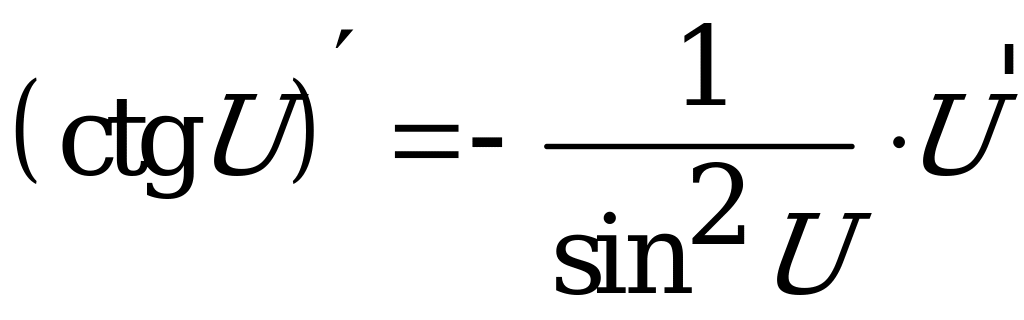 .
.
Основные правила дифференцирования
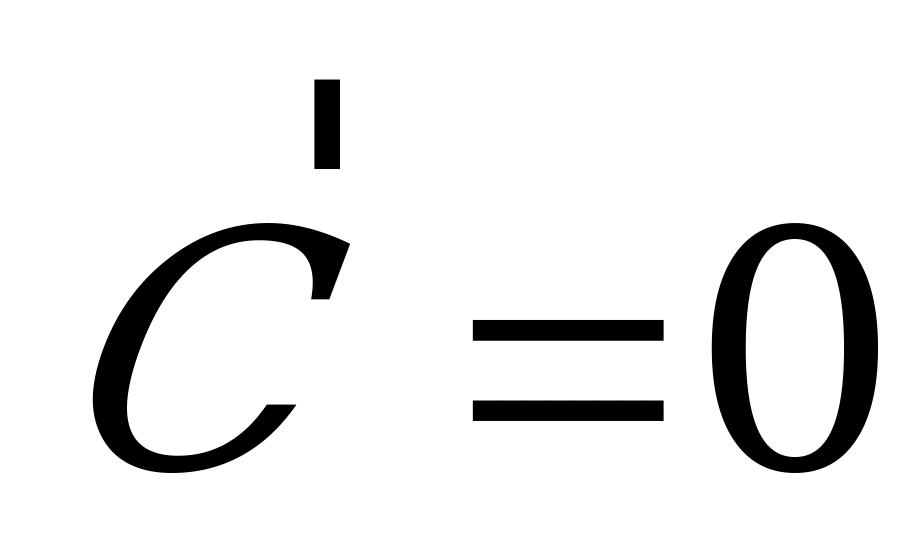 , где
, где 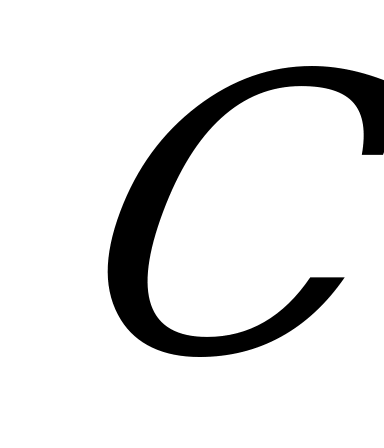 – const.
– const.
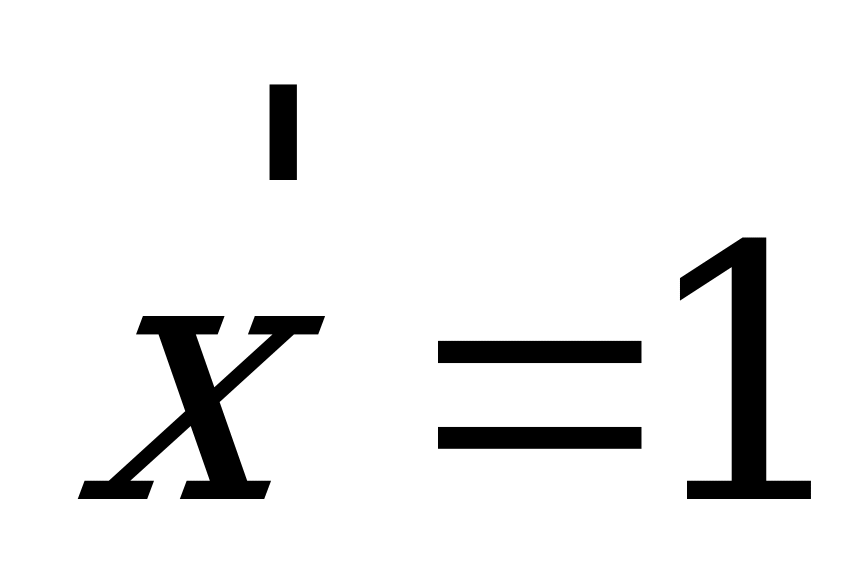 .
.
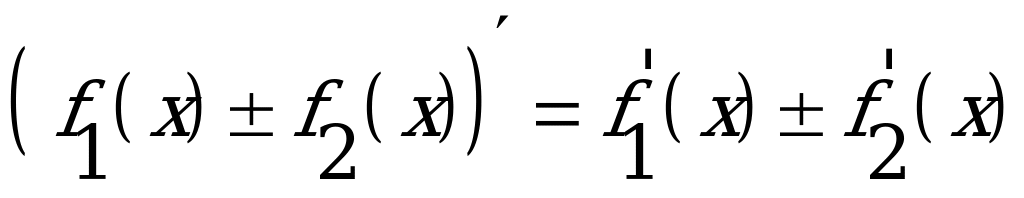 .
.
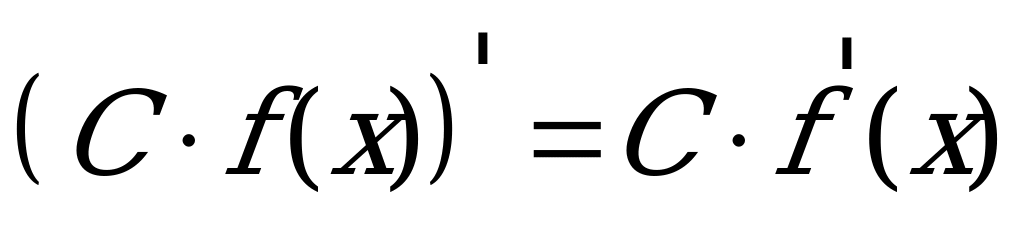 , где
, где 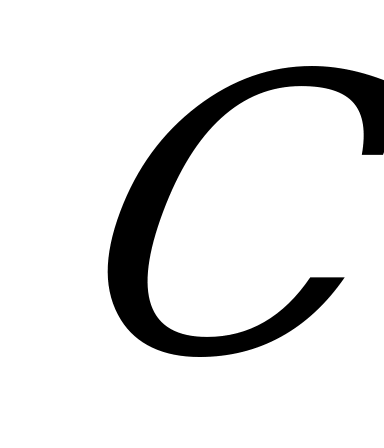 – const.
– const.
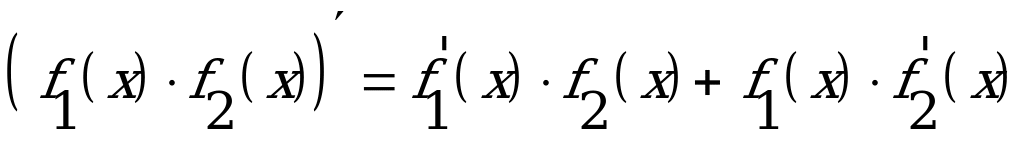
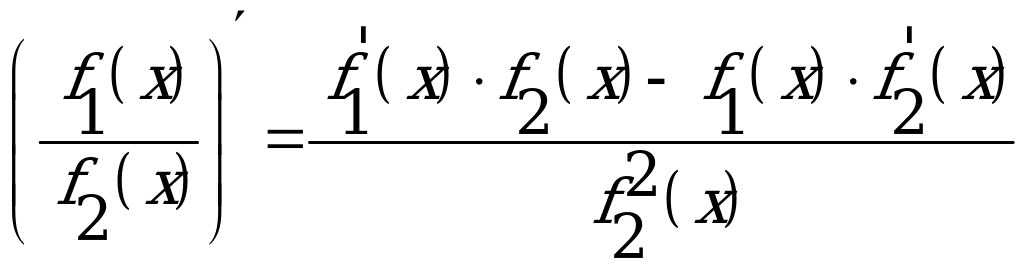 , (
, (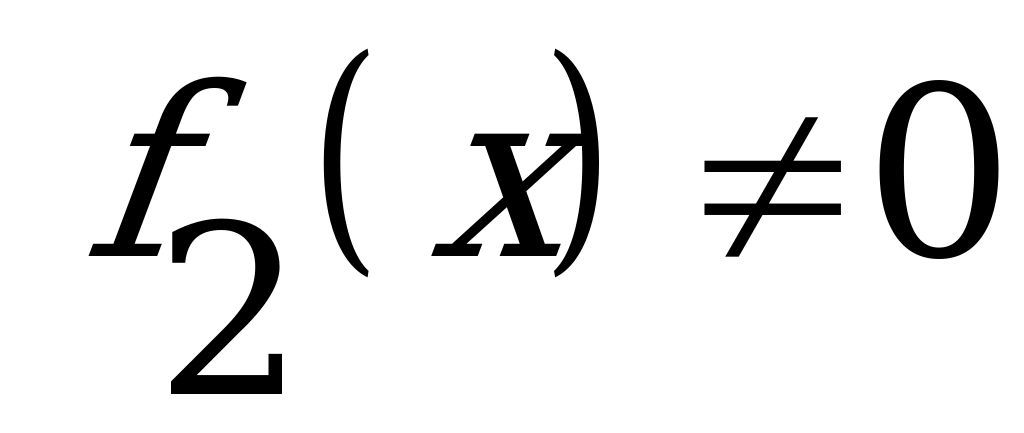 )
)
Вычислить производную функции:

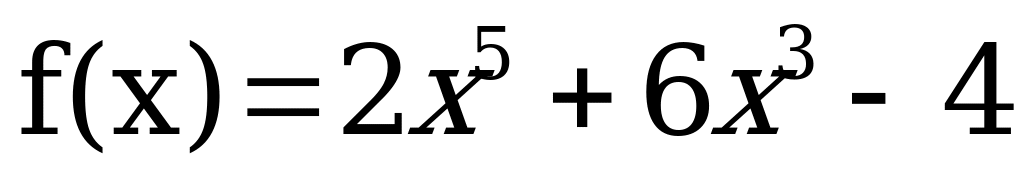
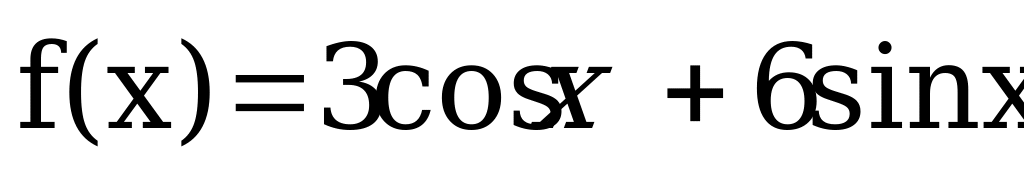
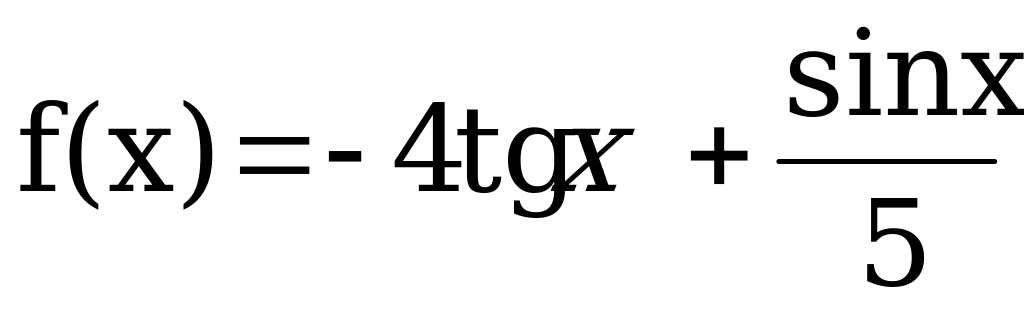
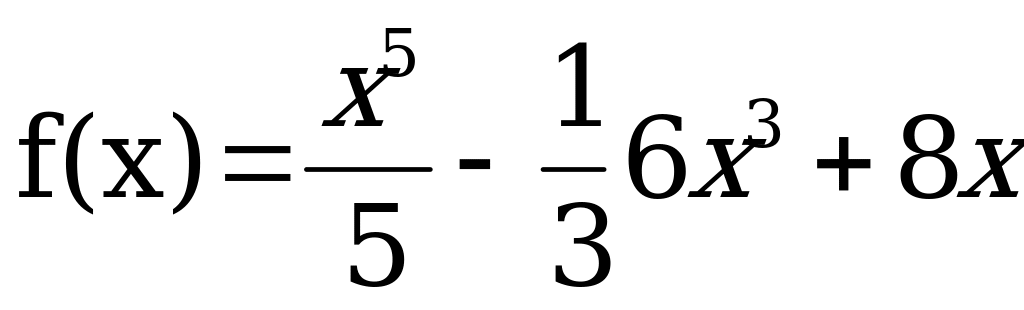
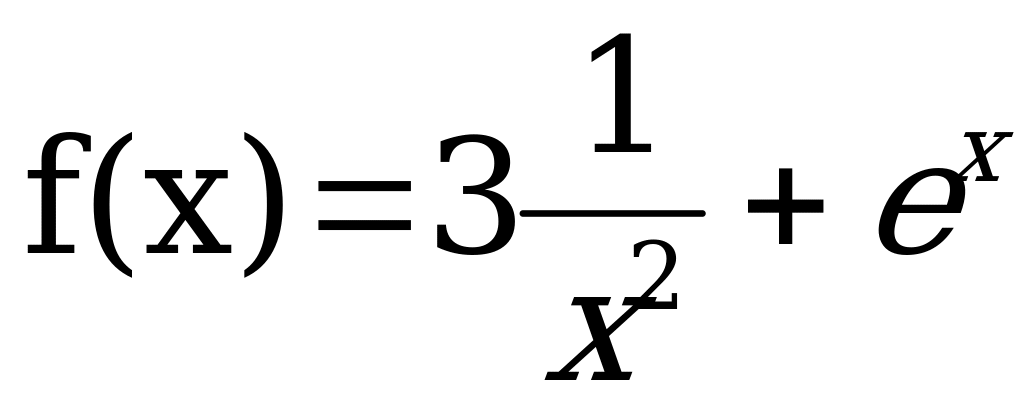
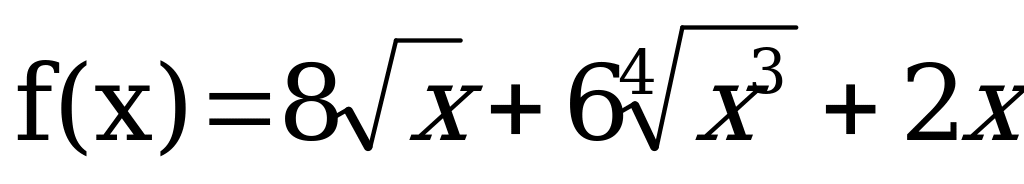
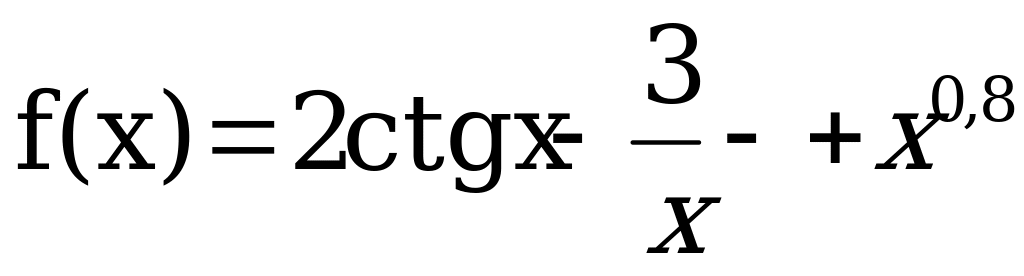
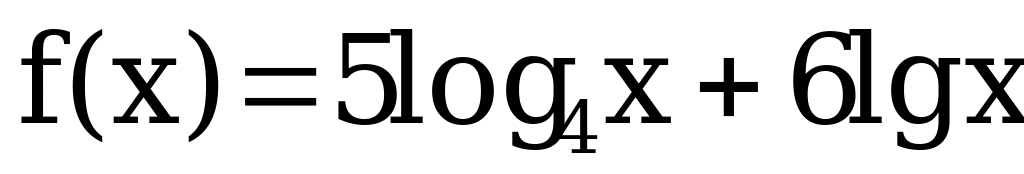
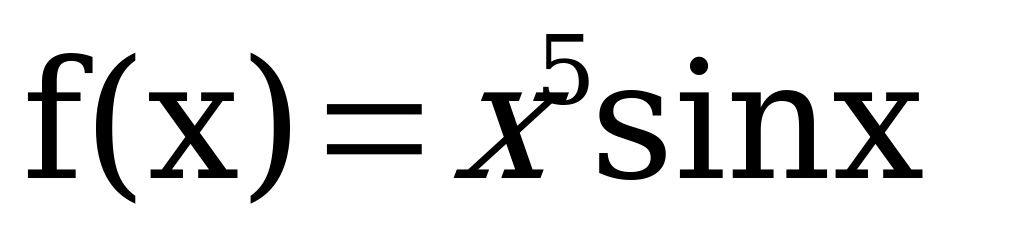
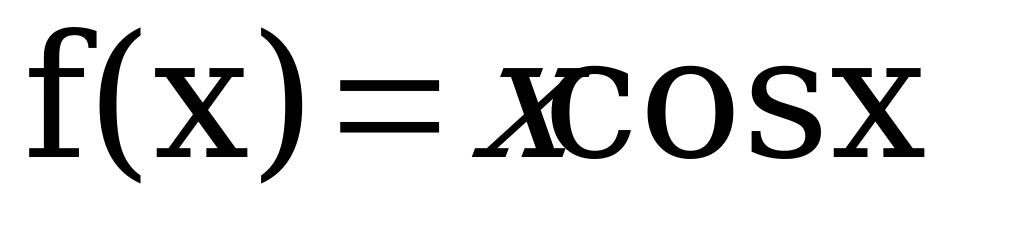
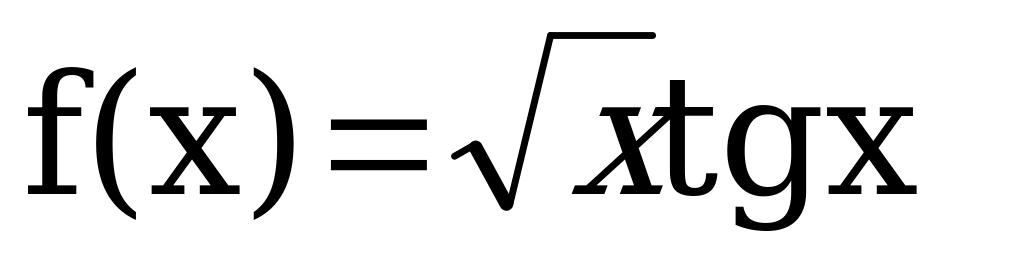
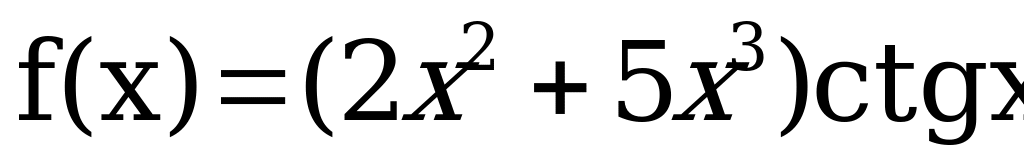
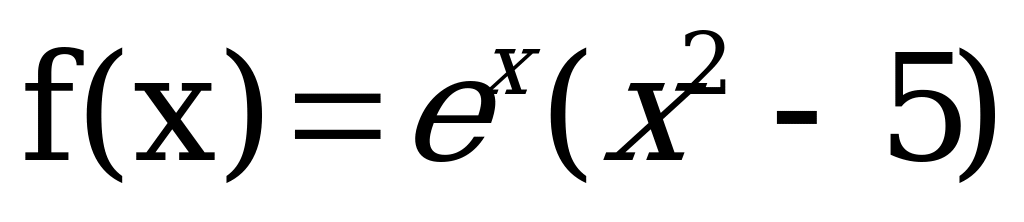
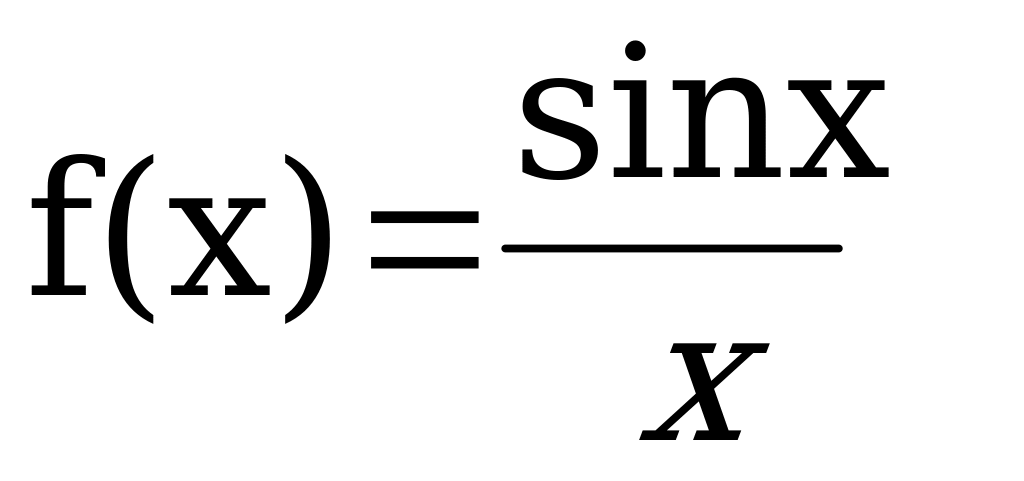
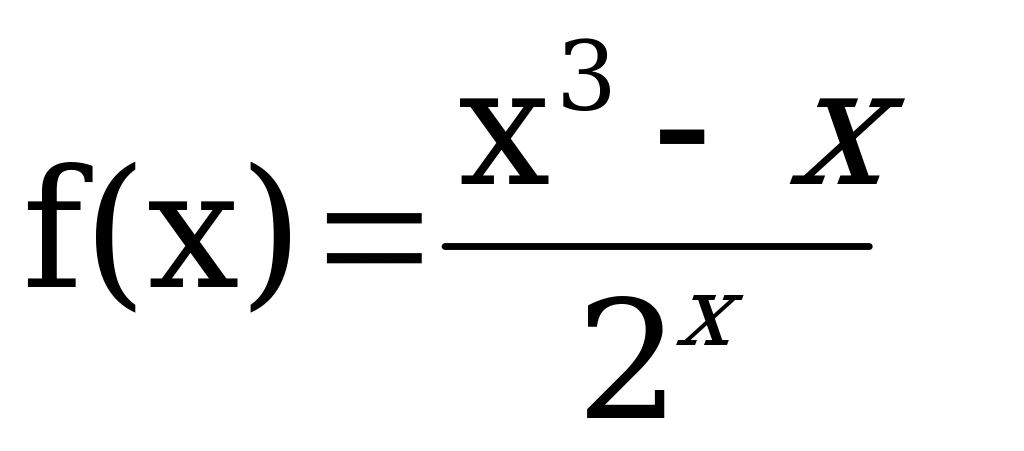
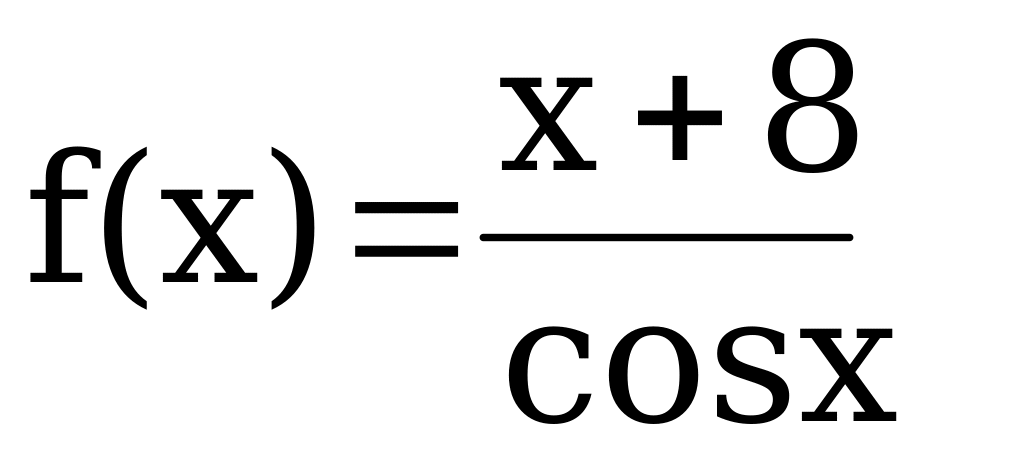
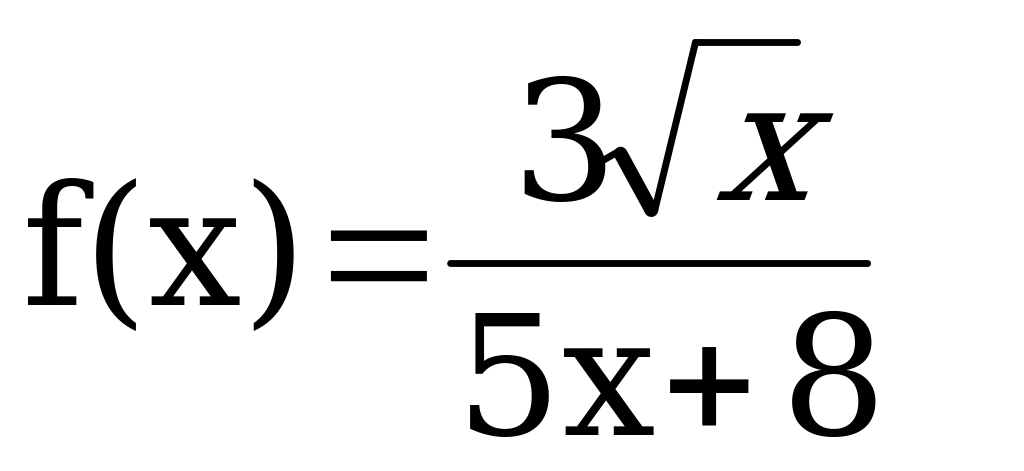
Решить уравнение:
f”(x) = 0, если 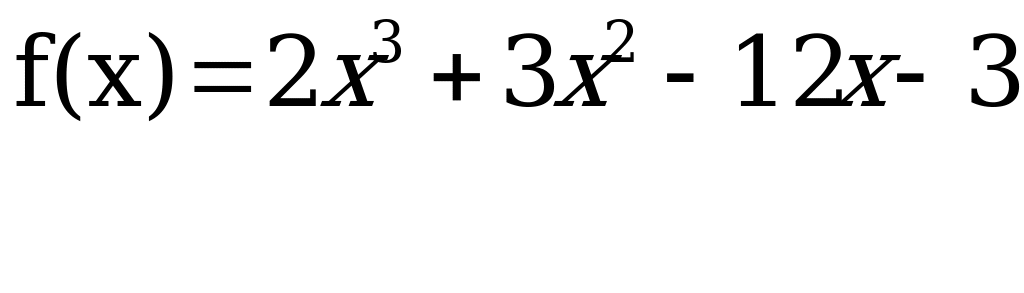
f”(x) = 2, если 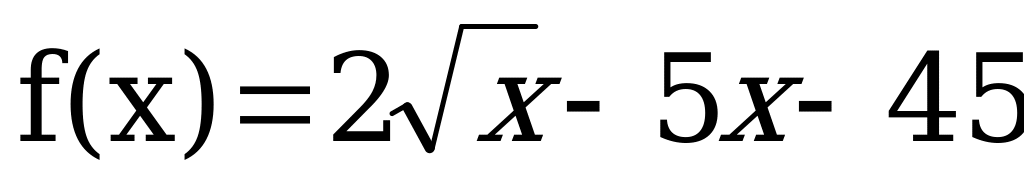
Решить неравенство:
f”(x) 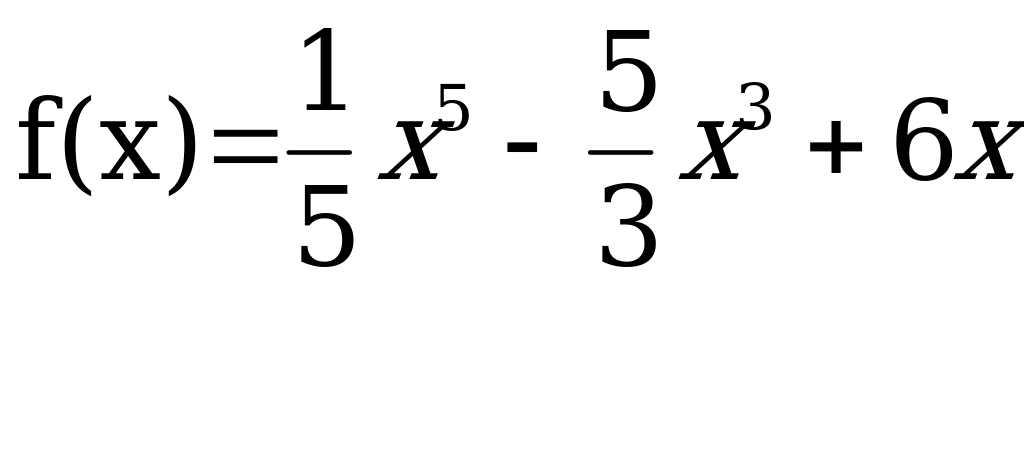
f”(x) 0, если 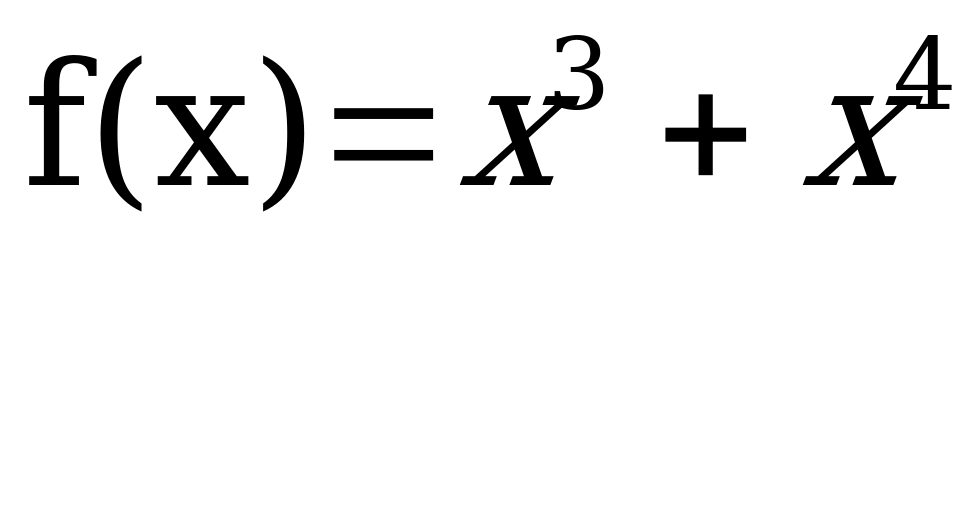
f”(x) 0, если 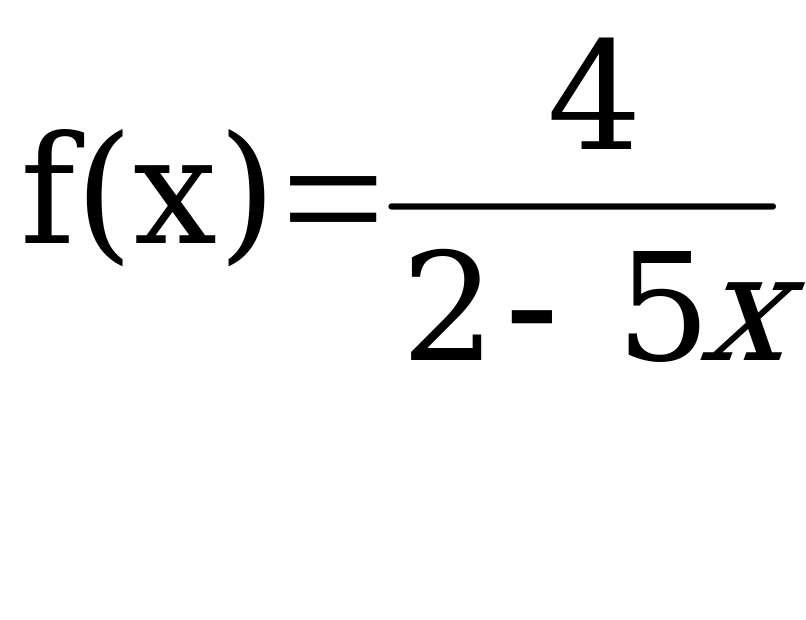
Справочный материал
Алгоритм исследования функции
и построения ее графика
Исследование функции проводится в следующей последовательности:
Находим область определения функции, точки разрыва, вертикальные асимптоты.
Находим точки пересечения графика функции с осями координат.
Исследуем четность функции.
Находим точки экстремума и значения функции в этих точках, интервалы монотонности.
Если необходимо, вычисляем значения функции в дополнительных токах (для уточнения графика).
На основании проведенного исследования строим график функции.
Провести полное исследование и построить график функции 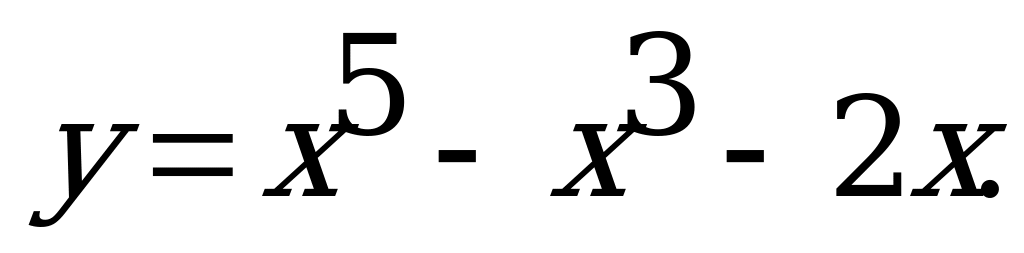
Провести полное исследование и построить график функции 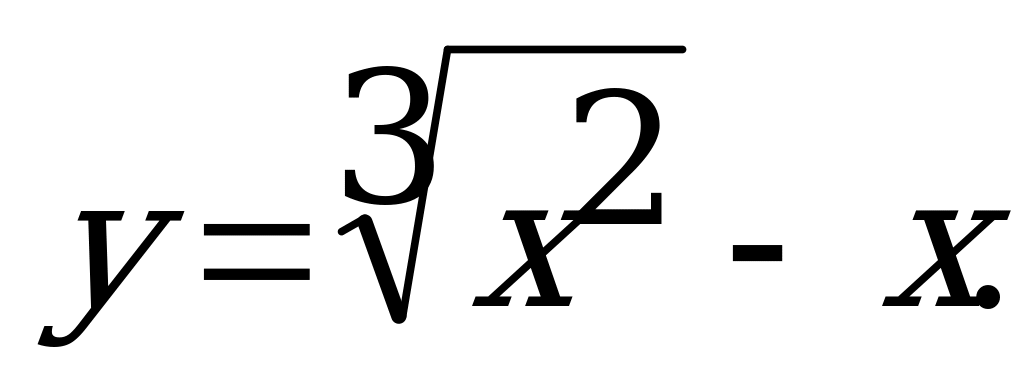
Провести полное исследование и построить график функции 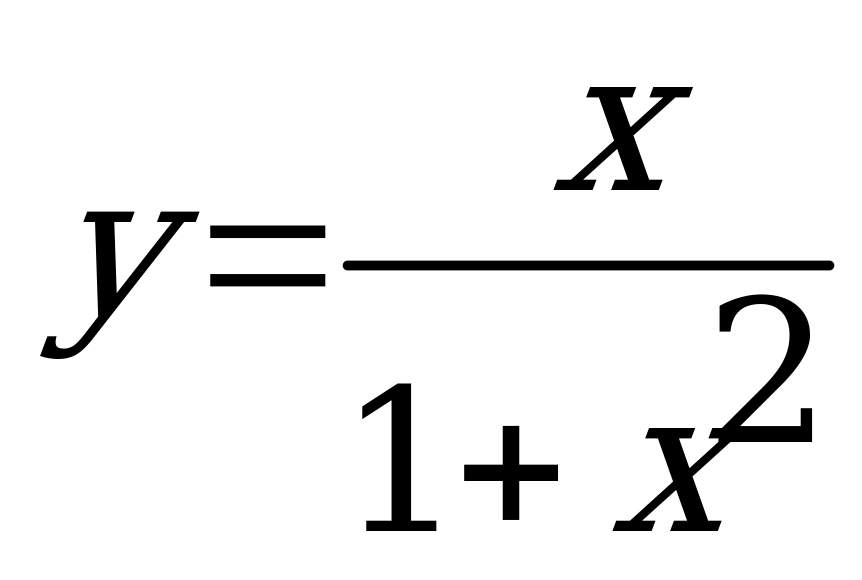
2.3 Многогранники и тела вращения,
площади поверхностей и объемы.
Справочный материал 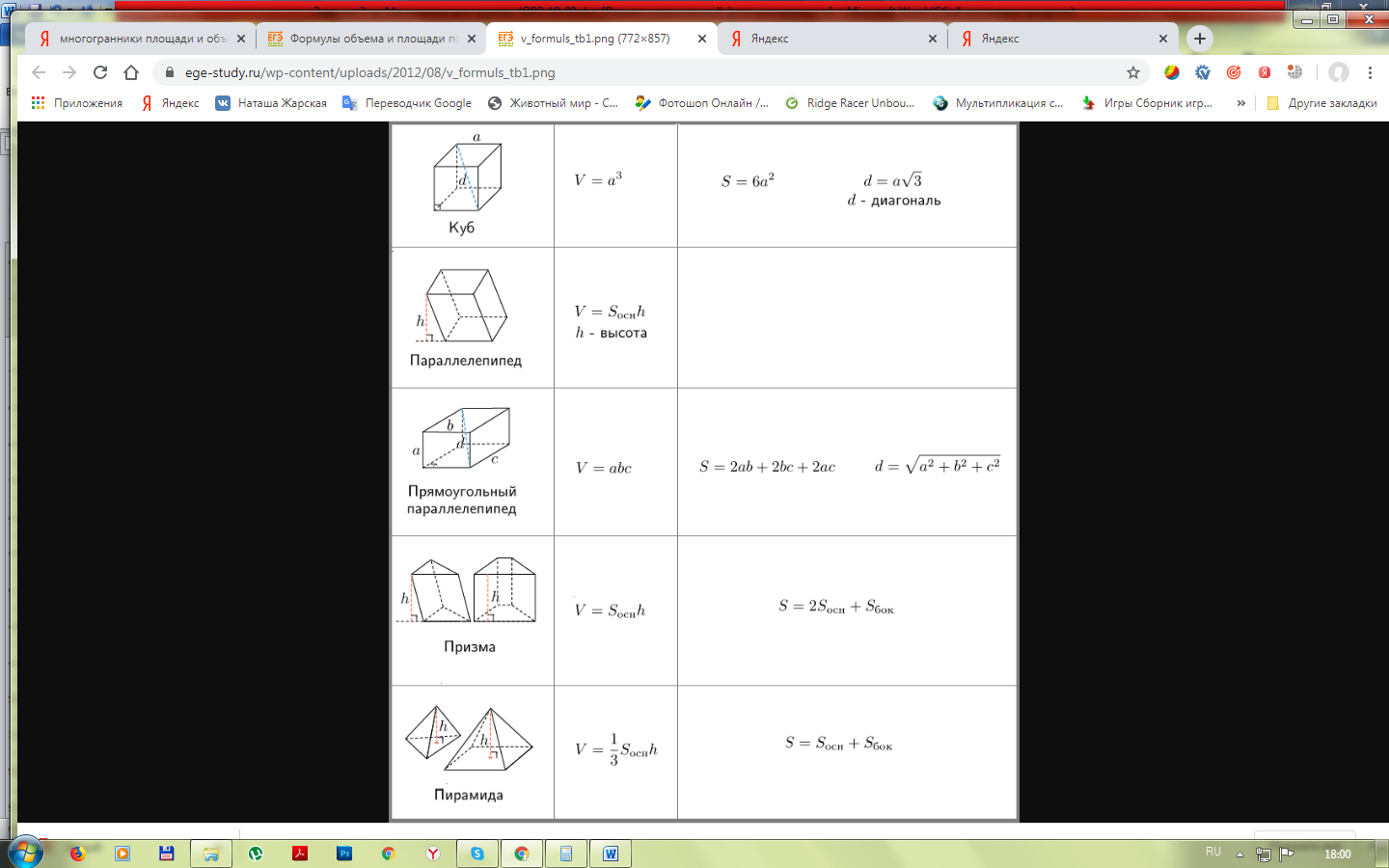
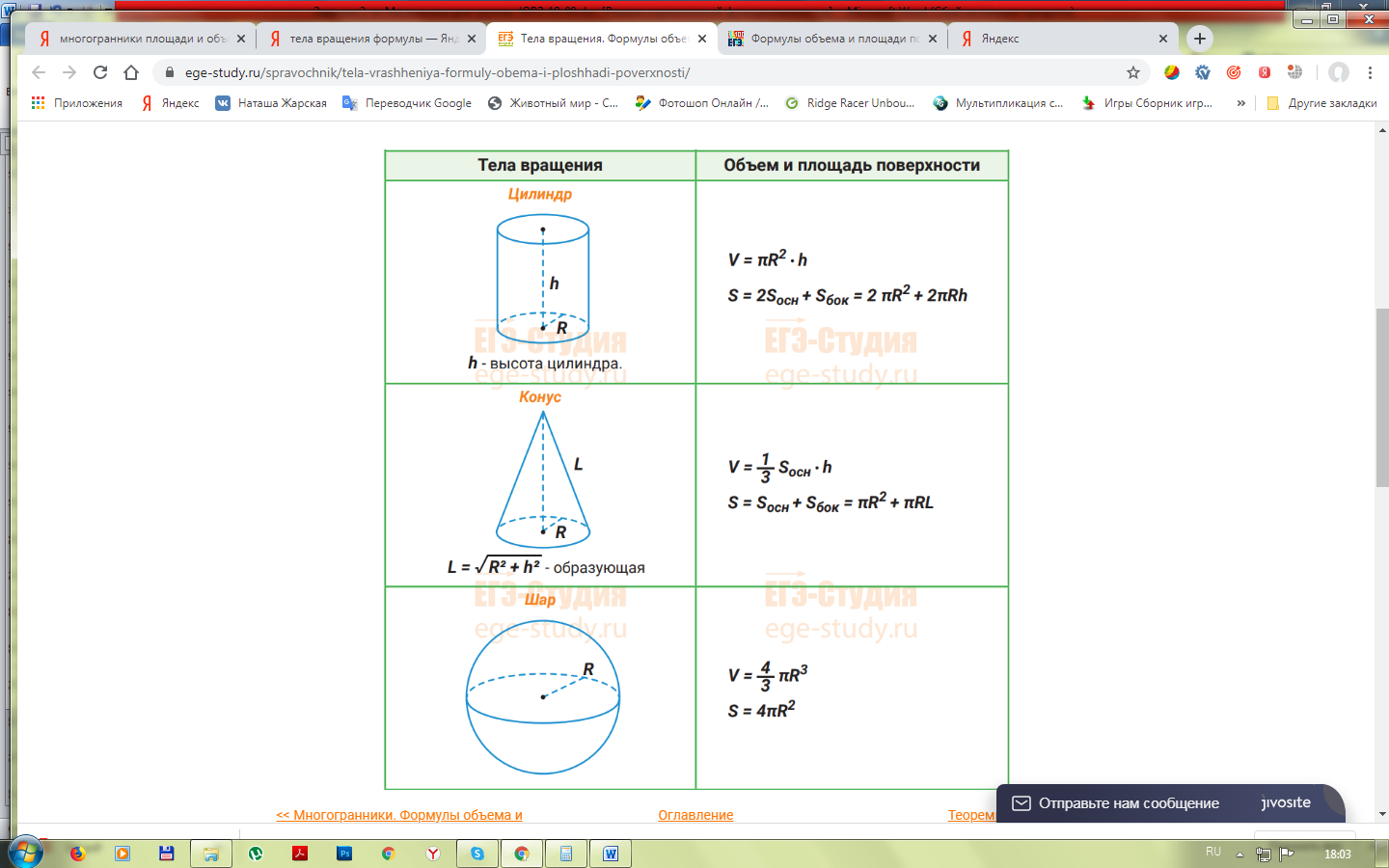
Решить задачи:
Основанием прямой четырехугольной призмы является ромб с диагоналями 1,6 дм и 3 дм, боковое ребро призмы равно 10 дм. Найдите площадь боковой и полной поверхности призмы.
Основанием прямой треугольной призмы является прямоугольный треугольник с катетами 0,7 см и 2,4 см, боковое ребро призмы равно 10 см. Найдите площадь боковой и полной поверхности призмы.
Основанием пирамиды является параллелограмм, стороны которого равны 20 см и 36 см, а площадь равна 360 см2. Высота пирамиды проходит через точку пересечения диагоналей основания и равна 12 см. Найдите площадь боковой поверхности пирамиды.
Основанием пирамиды является параллелограмм со сторонами 5 м и 4 м и меньшей диагональю 3 м. Высота пирамиды проходит через точку пересечения диагоналей основания и равна 2 м. Найдите площадь полной поверхности пирамиды.
Основанием пирамиды DABC является треугольник ABC, у которого АВ = АС= 13 см, ВС=10 см; ребро AD перпендикулярно к плоскости основания и равно 9 см. Найдите площадь боковой поверхности пирамиды.
Найдите объем куба ABCDA1B1C1D1 если: а) АС= 12 см; б) AC1 =3√2; в) DE= 1 см, где Е — середина ребра АВ.
Найдите объем прямоугольного параллелепипеда ABCDA1B1C1D1, если AC1 = 13 см, BD= 12 см и ВС1 = 11 см.
Найдите объем прямой призмы АВСA1B1C1 и если ∠BAC = 90°, ВС =37 см, АВ = 35 см, AA1 = 1,1 дм.
Пусть V, г и h соответственно объем, радиус и высота цилиндра. Найдите: а) V, если r = 2√2 см, h = 3 см; б) r, если V =120 см3, h = 3,6 см; в) h, если r = h, V = 8π см3.
Площадь основания цилиндра равна Q, а площадь его осевого сечения равна S. Найдите объем цилиндра.
Найдите объем пирамиды с высотой h, если: a) h = 2 м, а основанием служит квадрат со стороной 3 м; б) h = 2,2 м, а основанием служит треугольник ABC, в котором АВ — 20 см, ВС = 13,5 см, ∠AВС = 30°.
Найдите объем правильной треугольной пирамиды, высота которой равна 12 см, а сторона основания равна 13 см.
Пусть h, г и V — соответственно высота, радиус основания и объем конуса. Найдите: а) V, если h = 3 см, r=1,5 см; б) h, если г = 4 см, V = 48πсм3; в) r, если h = m, V = p.
Найдите объем конуса, если площадь его основания равна Q, а площадь боковой поверхности равна Р.
Найдите объем конуса, если его образующая равна 13 см, а площадь осевого сечения равна 60 см2.
Пусть V —объем шара радиуса R, a S — площадь его поверхности. Найдите: а) S и V, если R = 4 см; б) R и S, если V = 113,04 см3; в) R и V, если S = 64π см2.
В цилиндрическую мензурку диаметром 2,5 см, наполненную водой до некоторого уровня, опускают 4 равных металлических шарика диаметром 1 см. На сколько изменится уровень воды в мензурке?
В цилиндр вписан шар. Найдите отношение объемов цилиндра и шара.






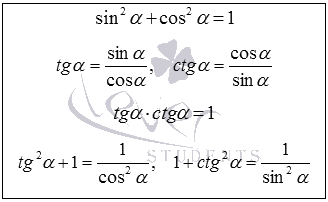
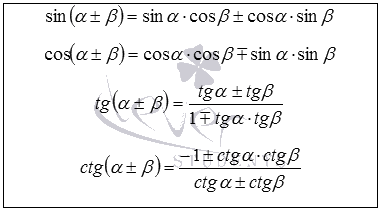
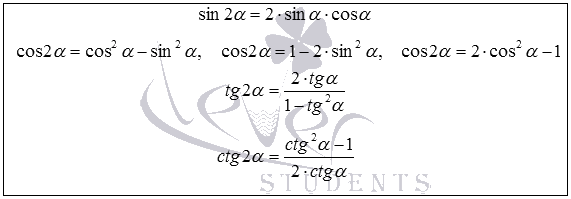








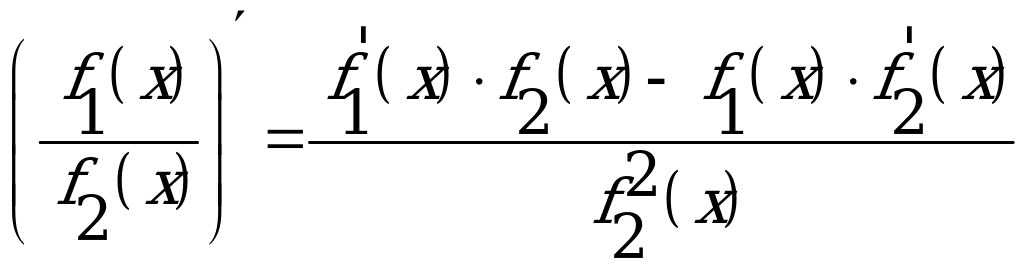 , (
, (