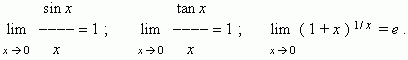Практическая работа
Вычисление пределов
Цель: формирование умений вычислять пределы последовательностей и функций,
раскрывать в простейших случаях неопределенности.
Методические рекомендации для выполнения практической работы по теме: Пределы числовых последовательностей
Предел числовой последовательности. Рассмотрим числовую последовательность, общий член которой приближается к некоторому числу a при увеличении порядкового номера n. В этом случае говорят, что числовая последовательность имеет предел. Это понятие имеет более строгое определение.
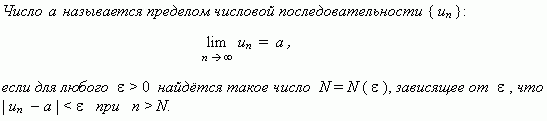
Это определение означает, что a есть предел числовой последовательности, если её общий член неограниченно приближается к a при возрастании n. Геометрически это значит, что для любого  0 можно найти такое число N, что начиная с n N все члены последовательности расположены внутри интервала ( a
0 можно найти такое число N, что начиная с n N все члены последовательности расположены внутри интервала ( a  a
a 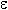 ). Последовательность, имеющая предел, называется сходящейся; в противном случае – расходящейся.
). Последовательность, имеющая предел, называется сходящейся; в противном случае – расходящейся.
Последовательность называется ограниченной, если существует такое число M, что | un | 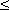 Mдля всех n . Возрастающая или убывающая последовательность называется монотонной.
Mдля всех n . Возрастающая или убывающая последовательность называется монотонной.
Основные свойства пределов. Нижеприведенные свойства пределов справедливы не только для числовых последовательностей, но и для функций.
Если { un } и { vn } две сходящиеся последовательности, то:
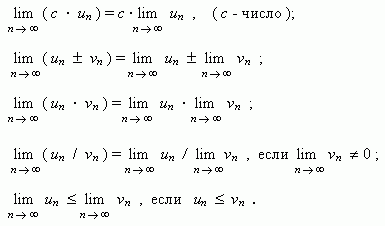
Если члены последовательностей { un }, { vn }, { wn } удовлетворяют неравенствам
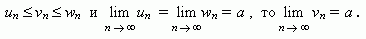
З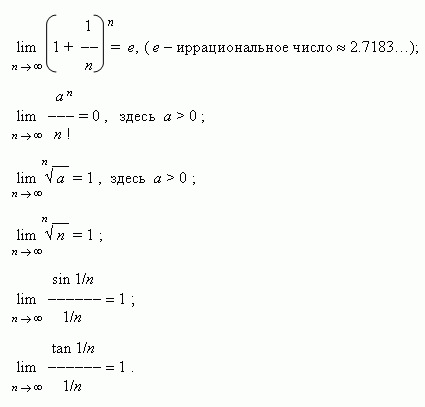 амечательные пределы
амечательные пределы
Предел функции. Число L называется пределом функции y = f ( x ) при x, стремящемся к a :
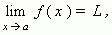
если для любого 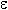 0 найдётся такое положительное число
0 найдётся такое положительное число 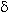 =
= 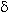 (
( 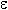 ), зависящее от
), зависящее от 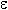 , что из условия | x - a |
, что из условия | x - a | 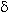 следует | f ( x ) – L |
следует | f ( x ) – L | 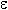 .
.
ПРИМЕР. Найти
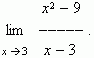
Решение. Подставляя x = 3 в выражение 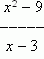 получим не имеющее смысла выражение
получим не имеющее смысла выражение 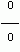 . Поэтому решим по-другому:
. Поэтому решим по-другому:
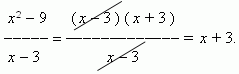
Сокращение дроби в данном случае корректно, так как x  3 , он лишь приближается к 3. Теперь мы имеем:
3 , он лишь приближается к 3. Теперь мы имеем:
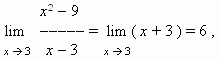 поскольку, если x стремится к 3, то x + 3 стремится к 6 .
поскольку, если x стремится к 3, то x + 3 стремится к 6 .
Замечательные пределы
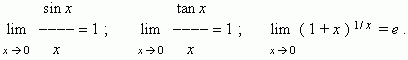
Бесконечно малая и бесконечно большая величины. Если предел некоторой переменной равен 0, то эта переменная называется бесконечно малой.
1.Найдите пределы последовательностей:
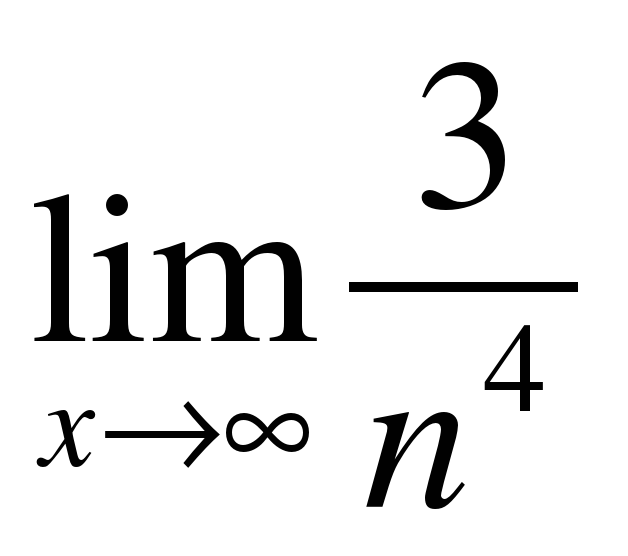 ; 3)
; 3) 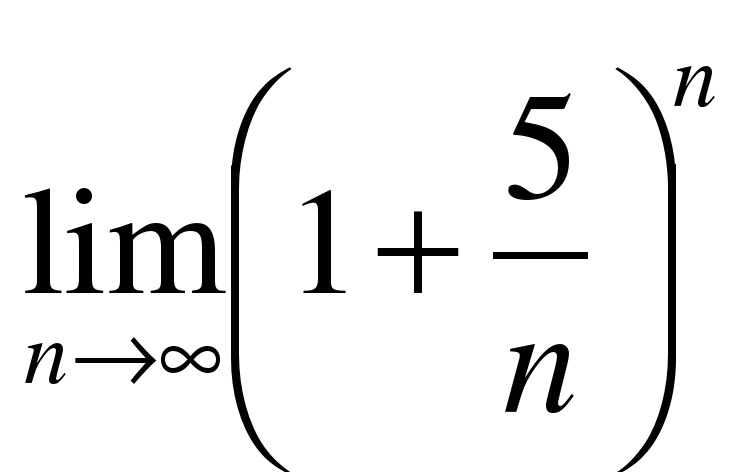 ;
;
; 4) .
2.Найдите пределы функций:
;
;
;
;
.
3. Раскрытие неопределенностей вида . Найдите пределы:
; ;
; .
Раскрытие неопределенностей вида . Найдите пределы:
; .
4







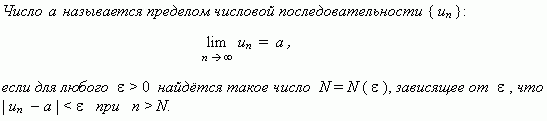
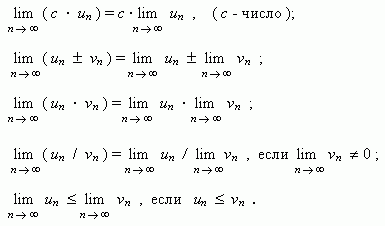
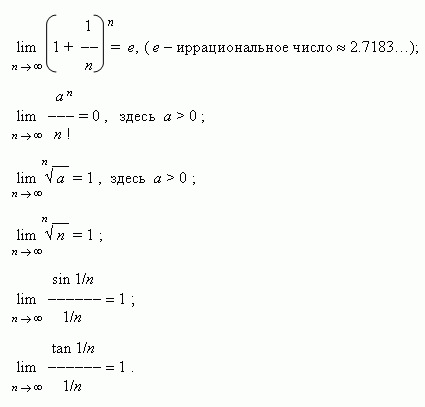 амечательные пределы
амечательные пределы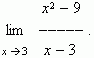
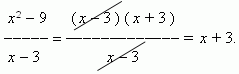
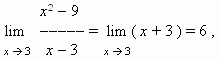 поскольку, если x стремится к 3, то x + 3 стремится к 6 .
поскольку, если x стремится к 3, то x + 3 стремится к 6 .