по МДК.01.02 Математический аппарат для построения компьютерных сетей (тема 1. Теория графов)
3) теперь для удобства «обратного хода» вершины можно отсортировать так, чтобы сначала шли все вершины, в которые можно доехать только из начальной точки А:
| 1 . На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К? 
| 2. На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Ж? 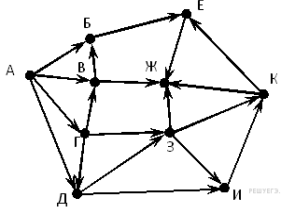
|
| 3. На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Ж?  | 4. На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К? 
|
| 5. На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К? 
| 6. На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К. По
каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К? 
|
| 7. На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Ж? 
| 8. На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К? 
|
| 9. На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Ж? 
| 10. На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К? 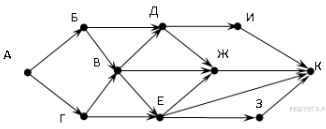
|
| 11 . На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Ж? 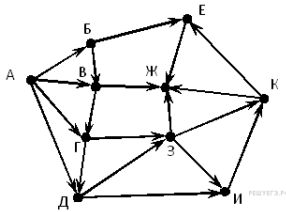
| 12. На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город З?  |
| 13. На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К? 
| 14. На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?  |
| 15. На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город З?  | 16. На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Ж?  |
| 17. На рисунке – схема дорог, связывающих города A, B, C, D, E, F, G H. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города A в город H? 
| 18. На рисунке – схема дорог, связывающих города A, B, C, D, E, F, G, H, K, L, M. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города A в город M? 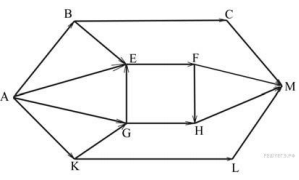
|
| 19. На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К, Л. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?  | 20. На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К, Л, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город M? 
|
| 21. На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К? 
| 22. На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город И? 
|
| 23. На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К? 
| 24. На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город И?  |
| 25. На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город И? 
| 26. На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город З? 
|
| 27. На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Е? 
| 28. На рисунке – схема дорог, связывающих города A, B, C, D, E, F, G, H, K, L, M. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города A в город E?  |
| 29. На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город З? 
| 30. На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К, Л. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К? 
|
В основе построения большинства алгоритмов на графах лежит систематический перебор вершин графа, при котором каждая вершина просматривается в точности один раз, а количество просмотров ребер графа ограничено заданной константой (лучше – не более одного раза). Один из основных методов проектирования графовых алгоритмов – это поиск (или обход графа) в глубину (depth first search, DFS), при котором начиная с произвольной вершины v
, ищется ближайшая смежная вершина v, для которой в свою очередь осуществляется поиск в глубину (т.е. снова ищется ближайшая, смежная с ней вершина) до тех пор, пока не встретится ранее просмотренная вершина, или не закончится список смежности вершины v (то есть вершина полностью обработана). Если нет новых вершин, смежных с v, то вершина v считается использованной, идет возврат в вершину, из которой попали в вершину v, и процесс продолжается до тех пор, пока не получим v = v
. Иными словами, поиск в глубину из вершины v основан на поиске в глубину из всех новых вершин, смежных с вершиной v. В алгоритме поиска в ширину (breadth first search, BFS). Обработка вершины v осуществляется путем просмотра сразу всех новых соседей этой вершины. При этом полученный путь является кратчайшим путем из одной вершины в другую. Методические рекомендации по выполнению и оформлению
1. Изучить инструкцию к практической работе.
2. Выполнить задание.
3. Оформить отчет.
1. Тема.
2. Цель.
4. Практическое задание.
5. Ответ на 1 контрольный вопрос (по указанию преподавателя).
Инструкционная карта составлена преподавателем: Шнарева Г.В.










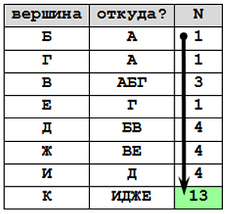 Б ← А Г ← А
Б ← А Г ← А







































