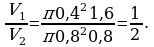Практикум по теме "Вычисление объемов тел и поверхностей вращения"

Практическое занятие

Вычисление объемов тел и поверхностей вращения

Цель работы:

студент должен:

знать:

- формулы объемов тел и поверхностей вращения;

уметь:

• вычислять объемы тел и поверхностей вращения.

Сведения из теории:

Объем прямоугольного параллелепипеда

V=abc,

где a, b, c – стороны параллелепипеда.

Объем куба

V=a³,

где a – длина грани куба.

Объем призмы

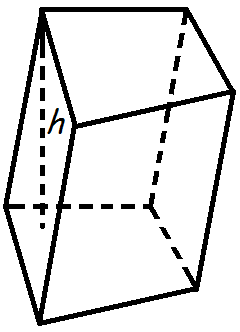
Рисунок 70. Призма

Объем призмы равен произведению площади основания призмы, на высоту:

V=S_oh,

где S_o – площадь основания призмы, h – высота призмы.

Объем параллелепипеда

Рисунок 71. Параллелепипед

Объем параллелепипеда равен произведению площади основания на высоту:

V=S_o·h,

где S_o – площадь основания, h – длина высоты.

Объем прямоугольного параллелепипеда

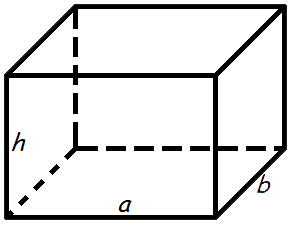
Рисунок 72. Прямоугольный параллелепипед

Объем прямоугольного параллелепипеда равен произведению его длины, ширины и высоты:

V=a·b·h,

где a – длина, b – ширина, h – высота.

Объем пирамиды

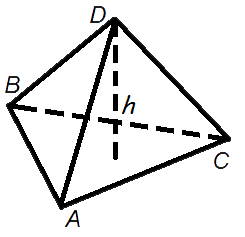
Рисунок 73. Пирамида

Объем пирамиды равен трети от произведения площади ее основания на высоту:

,

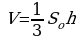где S_o – площадь основания пирамиды, h – длина высоты пирамиды.

Объем правильного тетраэдра

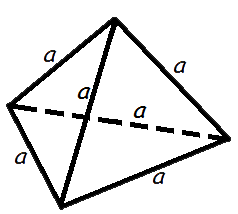
Рисунок 74. Тетраэдр

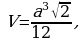
где a – длина ребра правильного тетраэдра.

Объем цилиндра

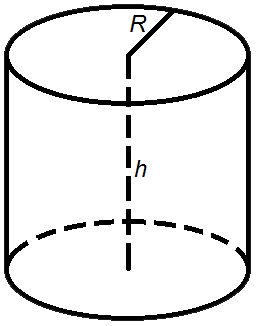
Рисунок 75. Цилиндр

Объем цилиндра равен произведению площади его основания на высоту:

V=πR²h

или

V=S_oh,

где S_o – площадь основания цилиндра, R – радиус цилиндра, h – высота цилиндра, π=3,141592.

Объем конуса

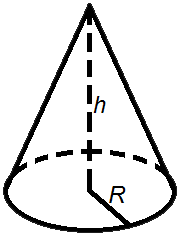
Рисунок 76. Конус

Объем конуса равен трети от произведения площади его основания на высоту:

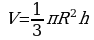
или

,

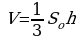где S_o – площадь основания конуса, R – радиус основания конуса, h – высота конуса, π=3,141592.

Объем шара

,

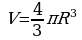где R – радиус шара, π=3,141592.

Пример 124.

Если каждое ребро куба увеличить на 2 см, то его объем увеличится на 98 см³. Определите ребро куба.

Решение:

обозначим ребро куба за х и составим уравнение:

(х+2)³=х³+98,
х³+6х²+12х+8=х³+98,
6х²+12х-90=0,
х²+2х-15=0,
х₁=-5, х₂=3.

х₁=-5 – не удовлетворяет условию задачи.

Ответ: 3.

Пример 125.

Прямоугольный лист жести, имеющий 1,6 м длины и 0,8 м ширины, можно согнуть в трубку двояким образом: в первом случае длина трубки будет 1,6 м, во втором 0,8 м. Найти отношение объемов трубок.

Решение:

трубки образуют цилиндры, объем, которого вычисляется по формуле:

V=πR²h.

У первого цилиндра высота будет 1,6 м, тогда радиус 0,4 м. Во втором цилиндре высота будет 0,8 м, тогда радиус 0,8 м. Вычислим отношение объемов двух цилиндров:

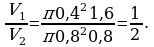
Ответ: 1:2.

Задания для самостоятельного решения:

Решите задачи:

1) Измерения прямоугольного параллелепипеда: 15 м, 50 м и 36 м. Найти ребро равновеликого ему куба.

2) Измерения прямоугольного бруса: 3 см, 4 см и 5 см. Если увеличить каждое его ребро на х см, то поверхность увеличится на 54 см². Как увеличится его объем?

3) Осевое сечение цилиндра – квадрат, диагональ которого равна 4. Найти объем цилиндра.

4) Основанием пирамиды служит прямоугольник со сторонами 9 м и 12 м, каждое из боковых ребер равно 12,5 м. Найти объем пирамиды.

5) Основанием пирамиды служит равнобедренный треугольник, у которого равные стороны по 6 см, а основание 8 см. Боковые ребра равны между собой и равны 9 см. Найти объем пирамиды.

6) В прямом параллелепипеде стороны основания равны 8 см и 15 см и образуют угол в 60⁰. Меньшая диагональ параллелепипеда составляем с плоскостью основания угол 30⁰. Найти объем параллелепипеда.

7) Высота и образующая конуса относятся как 4:5, а объем конуса равен 96π см³. Найти полную поверхность конуса.

Контрольные вопросы:

1. Запишите формулы объемов тел и поверхностей вращения.
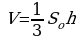
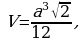
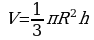
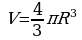