Инструкционная карта № 17
Тақырыбы/ Тема: «Правила вычисления производной».
Мақсаты/ Цель:
1.Обеспечить усвоение учащимися правил вычисления производной, перевести эти правила с теоретического уровня на практическое применение.
2. При решении упражнений, развивать у учащихся умения выделять главное, существенное в изучаемом материале, обучить умению рационально находить правильное решение изучаемого вопроса.
3. Развивать самостоятельность и рациональность при решении упражнений, развивать логику мышления.
Теоретический материал:
Правило 1: Если функции U и V дифференцируемы в точке х0, то их сумма дифференцируема в этой точке и
(U V)’=U’
V)’=U’ V’ (1)
V’ (1)
Коротко говорят: производная суммы равна сумме производных.
Пример1. Найдите производные функций: у=х2+3х, для нахождения у’ применим правило 1. Зная (х2)’=2х и (kx)’=k, получим у’=(х2+3х)’=(х2)’+(3х)’=2х+3.
Правило 2: Если функции U и V дифференцируемы в точке х0, то их произведение дифференцируемо в этой точке и
(UV)’=U’V+UV’ (2)
Следствие: Если функция U дифференцируема в точке х0, а С- постоянная, то функция CU дифференцируема в этой точке и (CU)’=CU’.
Коротко говорят: постоянный множитель можно выносить за знак
производной, т.е. (3х)’=3(x)’=3.
Пример 2. Найдите производные функций: f(x)=(3x-2)(5x+8) находим по правилу 2, вот так: f’(x)=((3x-2)(5x+8))’=(3x-2)’(5x+8)+(3x-2)(5x+8)’=(3-0)(5x+8)+(3x-2)(5+0)= =3(5x+8)+(3x-2)5=15x+24+15x-10=30x+14.
Правило 3: Если функции U и V дифференцируемы в точке х0 и функция V не
равна нулю, то частное  также дифференцируемо в этой точке х0 и
также дифференцируемо в этой точке х0 и
 (3)
(3)
Пример 3. Найдите производные функций: f(x)= по правилу 3, найдем так: f’(x)=
по правилу 3, найдем так: f’(x)= ’=
’= =
=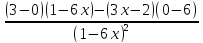 =
= = =
= = =
= .
.
Практическая часть:
I вариант Найдите производные функций:
а)у=х5+4х3-7х+6; г) у=  ; ж) у=(7-х2)
; ж) у=(7-х2) ; к) у=4-х-2,7+
; к) у=4-х-2,7+ ;
;
б) у= ; д) у= (2х2-3х+2)(5+3х-4х2); з) у=
; д) у= (2х2-3х+2)(5+3х-4х2); з) у=  ; л) у=
; л) у= (2х3-5х);
(2х3-5х);
в) у= е) у=
е) у=  -
-  +2; и) у=х-6+4х4-7х; м) у=
+2; и) у=х-6+4х4-7х; м) у=  .
.
II вариант Найдите производные функций:
а) у=x8-3х2+8х-5; г) у= ; ж) у=
; ж) у=  (7-х3); к) у=х1,3-2х-7+3;
(7-х3); к) у=х1,3-2х-7+3;
б) у=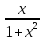 ; д) у=(3х2-7х+2)(1-2х-5х2); з) у=
; д) у=(3х2-7х+2)(1-2х-5х2); з) у=  л) у=
л) у= (4х + х4);
(4х + х4);
в) у=х3(8-х); е) у= - х-5+2х; и) у=
- х-5+2х; и) у=  +
+ - х5; м) у=
- х5; м) у= 
III вариант Найдите производные функций:
а) у=х4-5х2+3х-2; г) у= (5х2-3х+1)(7+4х-2х2); ж) у=  к) у= (6-х2)
к) у= (6-х2)
б) у= ; д) у= х-7+
; д) у= х-7+ -9х; з) у= (х4+х)
-9х; з) у= (х4+х) ; л) у=
; л) у=
в) у=х3(x-2x2); е) у=  и) у=
и) у=  +
+ -
-  м) у=2х3,4+х-5-
м) у=2х3,4+х-5-
IV вариант Найдите производные функций:
а) у=х9+8х6-5х+1; г) у=(х3-5х)(8х2+1); ж) у= к) у=
к) у=  (7+х2);
(7+х2);
б) у= д) у=х-4-
д) у=х-4- +
+ ; з) у=(
; з) у=( л) у=
л) у= 
в) у=х2(4+x); е) у=  и) у=
и) у= - х-7+8х2; м) у= 4х4-3х-3,2+
- х-7+8х2; м) у= 4х4-3х-3,2+
Контрольные вопросы:
Как вычисляется производная, если количество слагаемых больше 2?
Какое условие должно выполняться при вычислении производной частного?
Как можно сформулировать правило нахождения производной Cf(x)?
Можно ли рассматривать производную частного как производную произведения двух функций?
Напишите основные правила нахождения производной.







 V)’=U’
V)’=U’ также дифференцируемо в этой точке х0 и
также дифференцируемо в этой точке х0 и  (3)
(3) по правилу 3, найдем так: f’(x)=
по правилу 3, найдем так: f’(x)= ’=
’= =
=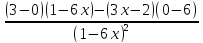 =
= = =
= = =
= .
.  ; ж) у=(7-х2)
; ж) у=(7-х2) ; к) у=4-х-2,7+
; к) у=4-х-2,7+ ;
; ; д) у= (2х2-3х+2)(5+3х-4х2); з) у=
; д) у= (2х2-3х+2)(5+3х-4х2); з) у=  ; л) у=
; л) у= (2х3-5х);
(2х3-5х); е) у=
е) у=  +2; и) у=х-6+4х4-7х; м) у=
+2; и) у=х-6+4х4-7х; м) у=  .
. ; ж) у=
; ж) у= 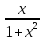 ; д) у=(3х2-7х+2)(1-2х-5х2); з) у=
; д) у=(3х2-7х+2)(1-2х-5х2); з) у=  л) у=
л) у=









