Преобразование графиков элементарных функций

Руководитель:

Синякова Елена Александровна

МБОУ СОШ №67

г.Владивосток

Оглавление

• Основные определения
• Основные характеристики функции
• Основные элементарные функции
• Преобразования графиков функций
• Порядок выполнения преобразования графиков функций

• Переменная у является функцией от переменной х, если задана такая зависимость между этими переменными, которая позволяет для каждого значения х однозначно определить значение у.
• Графиком функции f называется множество точек плоскости с координатами (х ;f(x)), где х пробегает область определения функции f.

0 (f(x) 4. Четность( f(x)=f(-x)) и нечетность( f(x)=-f(x)) . 5 .Точки экстремума, т.е. точки, лежащие внутри области определения, в которых функция принимает самое большое(максимум) или самое маленькое(минимум) значение по сравнению со значениями в близких точках. 6 .Промежутки монотонности, т.е. промежутки, на которых функция или возрастает, или убывает. 7.Наибольшее и наименьшее значение функции(по сравнению со всеми возможными точками). 8.Область значений функции, т.е. множество чисел, состоящее из всех значений функции. " width="640"

Основные характеристики функции

1.Область определения, т.е. множество значений аргумента, при которых задана функция.

2.Корни, т.е. точки, в которых функция обращается в нуль, или иначе решение уравнения f(x)=0.

1.Проекция графика на ось х .

2.Точки пересечения графика с осью х.

3.Участки оси х, соответствующие точкам графика, лежащим выше (ниже) оси х.

4.Симметричность относительно оси у или начала координат.

5. ” Вершины ” на графике функции.

6.Участки оси х, где график идет вверх или вниз.

7.Ординаты самой высокой и самой низкой точек графика.

8.Проекция графика на ось у.

3 .Промежутки постоянного знака, т.е. промежутки, на которых функция положительна(отрицательна), или иначе решение неравенства f(x)0 (f(x)

4. Четность( f(x)=f(-x)) и нечетность( f(x)=-f(x)) .

5 .Точки экстремума, т.е. точки, лежащие внутри области определения, в которых функция принимает самое большое(максимум) или самое маленькое(минимум) значение по сравнению со значениями в близких точках.

6 .Промежутки монотонности, т.е. промежутки, на которых функция или возрастает, или убывает.

7.Наибольшее и наименьшее значение функции(по сравнению со всеми возможными точками).

8.Область значений функции, т.е. множество чисел, состоящее из всех значений функции.

Основные элементарные функции

• Y=kx+b - линейная функция
• Y=k/x - обратная пропорциональность
• Y=ax 2 +bx+c - квадратичная функция
• Y=sin x - тригонометрическая функция
• Y=cos x - тригонометрическая функция
• Y=tg x - тригонометрическая функция
• Y=a x - показательная функция
• Y=log a x - логарифмическая функция

0, b=5. 1.Область определения - множество всех действительных чисел . 2. Область значений – множество R. 3.Функция возрастает на R , если k0 , убывает, если k4. Графиком функции является прямая линия. 5.Если k=0 , графиком функции является прямая , параллельная оси Ох. " width="640"

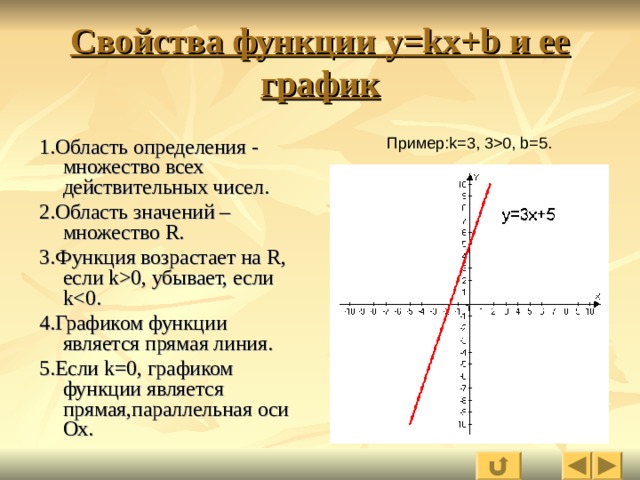
Свойства функции у =kx+b и ее график

Пример :k=3, 30, b=5.

1.Область определения - множество всех действительных чисел .

2. Область значений – множество R.

3.Функция возрастает на R , если k0 , убывает, если k

4. Графиком функции является прямая линия.

5.Если k=0 , графиком функции является прямая , параллельная оси Ох.

0. 1. Область определения : все действительные числа, кроме 0. 2. Область значений : все действительные числа, кроме 0. 3. Функция возрастает при k0. 4. Функция нечетная, т.к. f(-x)=-f(x). 5. Графиком функции является гипербола. " width="640"

Свойства функции у = k/ х и ее график

Пример :k=3, k0.

1. Область определения : все действительные числа, кроме 0.

2. Область значений : все действительные числа, кроме 0.

3. Функция возрастает при k0.

4. Функция нечетная, т.к. f(-x)=-f(x).

5. Графиком функции является гипербола.

0, вниз при aПример :a=2, b=3, c=-5. " width="640"

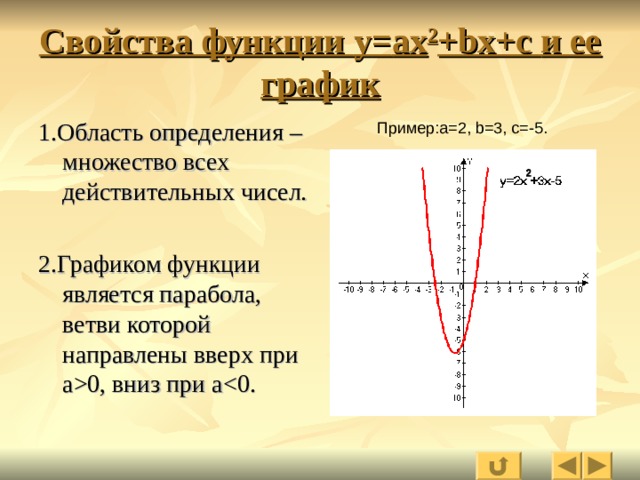
Свойства функции y= ах 2 + bx+c и ее график

1. Область определения – множество всех действительных чисел.

2. Графиком функции является парабола, ветви которой направлены вверх при а 0, вниз при a

Пример :a=2, b=3, c=-5.

Свойства функции y=cos x и ее график

1.Область определения – множество R всех действительных чисел .

2 .Множество значений – отрезок [-1;1].

3. Функция y=cos x периодическая с периодом 2П .

4. Функция y=cos x четная.

5.Функция y=cos x принимает :

• значение, равное 0, при х = П/2+П n , n- целое.
• наибольшее значение, равное 1, при х = 2П n , n- целое.
• наименьшее значение, равное -1, при х = П+2П n , n- целое.
• положительные значения на интервале(-П/2,П/2) и на интервалах, получаемых сдвигами этого интервала на 2П n , n -целое.
• отрицательные значения на интервале(П/2 ;3 П/2) и на интервалах, получаемых сдвигами этого интервала на 2П n , n -целое.

6.Функция y=cos x:

• возрастает на отрезке [ П ; 2П ] и на отрезках, получаемых сдвигами этого отрезка на 2П n , n- целое.
• убывает на отрезке [ 0 ; П ] и на отрезках, получаемых сдвигами этого отрезка на 2П n , n- целое.

Свойства функции y=sin x и ее график

1.Область определения – множество R всех действительных чисел .

2 .Множество значений – отрезок [-1;1].

3. Функция y=sin x периодическая с периодом 2П .

4. Функция y=sin x нечетная.

5.Функция y=sin x принимает :

• значение, равное 0, при х = П n , n- целое.
• наибольшее значение, равное 1, при х =П/2+2П n , n- целое.
• наименьшее значение, равное -1, при х = -П/2+2П n , n- целое.
• положительные значения на интервале(0 ; П) и на интервалах, получаемых сдвигами этого интервала на 2П n , n -целое.
• отрицательные значения на интервале(П ; 2П) и на интервалах, получаемых сдвигами этого интервала на 2П n , n -целое.

6.Функция y=sin x:

• возрастает на отрезке [ -П/2 ; П/2 ] и на отрезках, получаемых сдвигами этого отрезка на 2П n , n- целое.
• убывает на отрезке [ П/2 ; 3П/2 ] и на отрезках, получаемых сдвигами этого отрезка на 2П n , n- целое.

Свойства функции y=tg x и ее график

1.Область определения – множество всех действительных чисел, кроме х = П/2+П n , n -целое.

2 .Множество значений – множество R всех действительных чисел .

3. Функция y=tg x периодическая с периодом П .

4. Функция y=tg x нечетная.

5.Функция y=tg x принимает :

• значение, равное 0, при х = П n , n- целое.
• положительные значения на интервалах ( П n; П/2+П n ), n- целое.
• отрицательные значения на интервалах ( -П/2+П n; П n ), n- целое.

6.Функция y=tg x возрастает на интервалах(-П/2+П n; П/2+П n) , n- целое .

1, и убывающей, если 0 Пример :a=3. " width="640"

Свойства функции у =a x и ее график

1.Область определения – множество R всех действительных чисел .

2 .Множество значений – множество всех положительных чисел .

3.Показательная функция y=a x является возрастающей на множестве всех действительных чисел, если a1, и убывающей, если 0

Пример :a=3.

0 , если a1, и убывающей, если 0 4. Если a1, то функция у =log a x принимает положительные значения при x1, отрицательные при 01. " width="640"

Свойства функции у =log a x и ее график

Пример :a=2.8

1.Область определения – множество всех положительных чисел .

2 .Множество значений – множество R всех действительных чисел .

3.Логарифмическая функция y=log a x является возрастающей на промежутке x0 , если a1, и убывающей, если 0

4. Если a1, то функция у =log a x принимает положительные значения при x1, отрицательные при 01.

Преобразования графиков функций

• Установим связь между графиками функций y =f(x) и …
• у = f(x-a)
• у = f(x) + b
• y = f(x-a) + b
• Y=f(|x|)
• Y=|f(x)|

0) или влево (если а 0). Примеры: у = 1/x, y=1/(x-3), y=1/(x+2) y=sin(x), y=sin(x-1), y=sin(x+0.5) y=2 x, y=2 (x+2) ,y=2 (x-3) " width="640"

График функции y=f(x-a)

• Для построения графика функции y=f(x-a) надо изобразить график исходной функции f(x) и сдвинуть его вдоль оси Ох на а единиц вправо (если а 0) или влево (если а 0).

Примеры:

• у = 1/x, y=1/(x-3), y=1/(x+2)
• y=sin(x), y=sin(x-1), y=sin(x+0.5)
• y=2 x, y=2 (x+2) ,y=2 (x-3)

y=2 x

Y=2 x-3

y=2 x+2

0) вдоль оси О y или вниз (если b ). Примеры: 1) у = 1/x, y=(1/x)-3, y=(1/x)+2 2) y=sin(x), y=sin(x)-3, y=sin(x)+2 3) Y=2 x ,y=2 x +1,y=2 x -3 " width="640"

График функций у = f(x) + b

• Для построения графика функции у = f(x) +b надо изобразить график функции y= f (х) и сдвинуть его на b единиц вверх (если b 0) вдоль оси О y или вниз (если b ).

Примеры:

1) у = 1/x, y=(1/x)-3, y=(1/x)+2

2) y=sin(x), y=sin(x)-3, y=sin(x)+2

3) Y=2 x ,y=2 x +1,y=2 x -3

y=2 x +1

y=2 x

y=2 x -3

0 ) или в лево (если a 0), и вдоль оси О y на b единиц вверх (если b0 ) или вниз (если b . НАПРИМЕР: 1) y=1/x; y=(1/(x-3))+2; y=(1/(x+1))-3 ) 2) y=sinx,y=sin(x-2)+3, y=sin(x-3)+2 3 ) y=2x,y=2 (x-3) +2,y=2 (x+2) -2 " width="640"

График функции y=f(x-a)+b

Для построения графика функции Y= f (x-a)+b

надо изобразить график исходной функции y= f (x) и сдвинуть его вдоль оси О x на a единиц в право(если a0 ) или в лево (если a 0), и вдоль оси О y на b единиц вверх (если b0 ) или вниз (если b .

НАПРИМЕР:

1) y=1/x; y=(1/(x-3))+2; y=(1/(x+1))-3 )

2) y=sinx,y=sin(x-2)+3, y=sin(x-3)+2

3 ) y=2x,y=2 (x-3) +2,y=2 (x+2) -2

y=2 x

Y=2 x-3 +2

y=2 x+2 -2

1 производится сжатие в k раз, при 0 k производится растяжение в k раз. При k 0 производится отображение графика относительно оси О y. НАПРИМЕР: 1) y=1/x; y=1/3x; y= - (1/x) 2) y=sin x ; y=sin( 2 x) ; y=sin( 0,4 x) 3) y=2x,y=2 0,4x ,y=2 3x " width="640"

График функции y= f ( k x)

▪ Для построения графика функции y= f ( k x) необходимо построить график исходной функции y= f (x) и растянуть или сжать его вдоль оси Ox .Если k 1 производится сжатие в k раз, при 0 k производится растяжение в k раз. При k 0 производится отображение графика относительно оси О y.

НАПРИМЕР:

1) y=1/x; y=1/3x; y= - (1/x)

2) y=sin x ; y=sin( 2 x) ; y=sin( 0,4 x)

3) y=2x,y=2 0,4x ,y=2 3x

y=2 x

y=2 0.4x

y=2 3x

0 ) или сжать(если 0 k 1 ) вдоль оси О y в k раз. Если k при этом отрицательное, то необходимо отобразить график относительно оси О x НАПРИМЕР: 1) y=1/x; y=2/x; y=- 3 /x 2)y=sin x; y=2sin x; y=0.6sin x 3)y=2x,y=2*2 x ,y=-3*2 x " width="640"

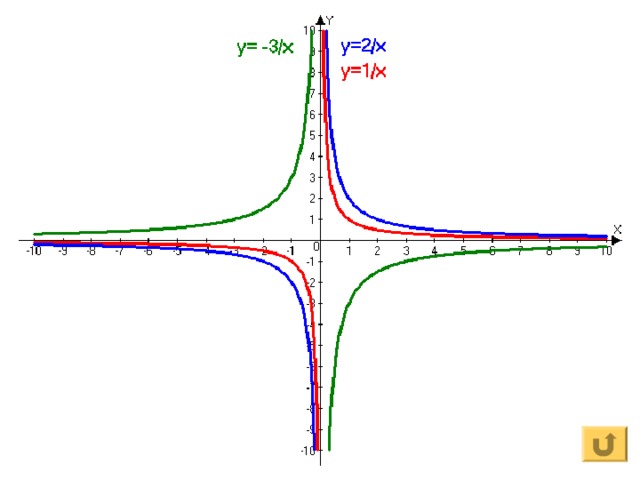
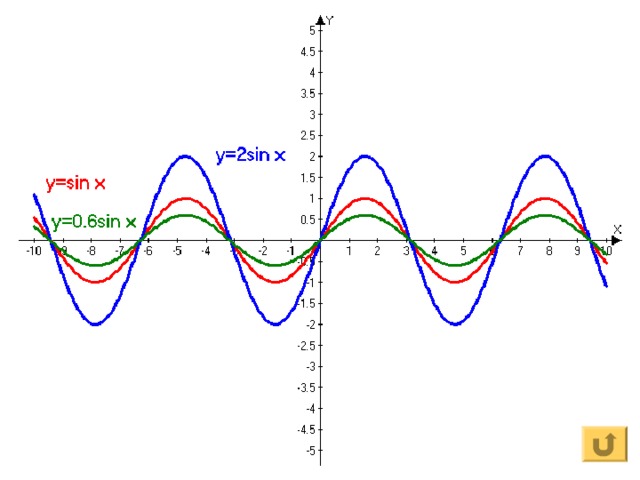
График функции y= kf (x)

▪ Для построения графика функции y= kf (x) исходный график y= f (x) нужно растянуть (если k 0 ) или сжать(если 0 k 1 ) вдоль оси О y в k раз. Если k при этом отрицательное, то необходимо отобразить график относительно оси О x

НАПРИМЕР:

1) y=1/x; y=2/x; y=- 3 /x

2)y=sin x; y=2sin x; y=0.6sin x

3)y=2x,y=2*2 x ,y=-3*2 x

y=2 x

y=2*2 x

y=-3*2 x

=0 , то |f(x)|=f(x)). Часть графика, лежащую ниже оси Ох, отразить симметрично относительно оси абсцисс(т.к. при f(x) Примеры : 1)y=sinx,y=|sinx| 2)y=1/x,y=|1/x| 3)y=2 x ,y=|2 x | " width="640"

График функции y=|f(x)|

Чтобы построить график функции y=|f(x)| , надо :

• Построить график базовой функции y=f(x) для всех х из ее области определения.
• Оставить без изменения ту часть графика, которая лежит выше оси Ох(т.к. если f(x)=0 , то |f(x)|=f(x)).
• Часть графика, лежащую ниже оси Ох, отразить симметрично относительно оси абсцисс(т.к. при f(x)

Примеры :

1)y=sinx,y=|sinx|

2)y=1/x,y=|1/x|

3)y=2 x ,y=|2 x |

y=2 x

y=|2x|

График функции y=f(|x|)

Чтобы построить график функции y=f(|x|) , надо :

• Построить график базовой функции y=f(x) .
• Оставить без изменения ту часть графика, которая лежит правее оси Oy.
• Часть графика функции y=f(x) , лежащую левее оси Oy, удалить, вместо нее построить часть графика, симметричную относительно оси Oy, оставленной неизменной части графика функции f.
• Примеры :
• 1)y=sinx,y=sin|x|
• 2)y=1/x,y=1/|x|
• 3)y=2 x ,y=2 |x|

y=2 |x|

y=2 x

Порядок выполнения преобразования графиков функций.

При выполнении преобразований графиков функций следует придерживаться следующих правил :

1. При выполнении преобразований вида y=f(ax+b) необходимо вынести множитель a в выражении ax+b за скобку, т.е. представить функцию в виде y=f(a(x+b/a)). Таким образом, параллельный перенос вдоль оси абсцисс будет проводиться не на |b| единиц, а на |b/a| единиц в нужном направлении.

2.Преобразования сжатия(растяжения ) выполняются всегда до преобразований сдвига(параллельного переноса) , т.е. обладают приоритетом.

3.При выполнении преобразований вида y=f(k|x|+b) удобно придерживаться следующего порядка действий :

• f(x) f(kx) ( преобразование сжатия)
• f(kx) f(k(x+b/k)) ( преобразование сдвига)
• Y=f(k(x+b/k)) y=f(k(|x|+b/k)) ( преобразование «модуль аргумента»).

4.При выполнении преобразований вида y=f|kx+b| стоит придерживаться следующего порядка действий :

• y=f(x) y=f(|x|) ( преобразование «модуль аргумента»)
• Y=f(|x|) y=f(|kx|) ( преобразование сжатия)
• Y=f(|kx|) y=f(|k(x+b/k)|) ( преобразование сдвига).