Россия, Воронеж
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 14.12.2021 19:07
Беляева Ирина Владимировна
учитель математики
45 лет
1 176
51 949 
Местоположение
Специализация
Преобразование графиков тригонометрических функций
Категория:
Математика
06.12.2021 22:37
Просмотр содержимого документа
«Преобразование графиков тригонометрических функций»
1 , то сжатие в k раз -если 0 k , то растяжение в 1/ k раз " width="640"
Характеристика преобразований графиков функций у= mf(x), y=f(kx) из графика функции y=f(x)
1. Если известен график функции y=f(x) , то график функции y=f(kx) строится посредством сжатия по оси О x исходного графика пропорционально коэффициенту k при аргументе, а именно:
-если k1 , то сжатие в k раз
-если 0 k , то растяжение в 1/ k раз
Растяжение (сжатие) в k раз вдоль оси OX
0 , то растяжение в k раз -если 0 k , то сжатие в 1/ k раз " width="640"
2. Если известен график функции y=f(x) , то график функции y=kf(x) строится посредством растяжения вдоль оси О y исходного графика, пропорционально коэффициенту в k раз, а именно:
-если m0 , то растяжение в k раз
-если 0 k , то сжатие в 1/ k раз
Растяжение (сжатие) в k раз вдоль оси OY
0 , то сдвиг на m единиц влево -если m , то сдвиг на m единиц вправо " width="640"
3. Если известен график функции y=f(x) , то график функции y=f(x + m ) строится посредством сдвига по оси О x исходного графика(координатной оси) на m единиц, а именно:
-если m0 , то сдвиг на m единиц влево
-если m , то сдвиг на m единиц вправо
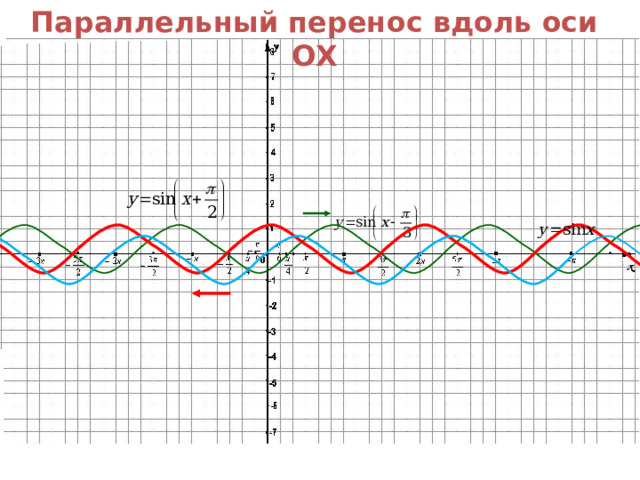
Параллельный перенос вдоль оси OX
0 , то сдвиг на m единиц вверх -если m , то сдвиг на m единиц вниз " width="640"
4. Если известен график функции y=f(x) , то график функции y=f(x )+ m строится посредством сдвига по оси О y исходного графика(координатной оси) на m единиц, а именно:
-если m0 , то сдвиг на m единиц вверх
-если m , то сдвиг на m единиц вниз
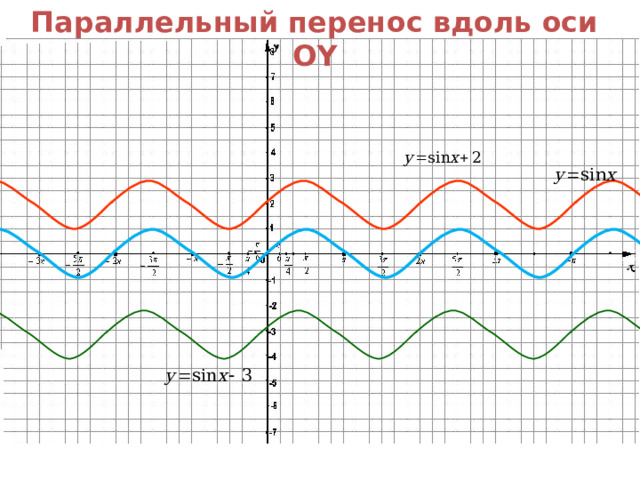
Параллельный перенос вдоль оси OY
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
