Преобразование симметрии в пространстве.

Дата проведения:

Преподаватель: Касымова У.Ш.

Группа:

Тема урока: Преобразование симметрии в пространстве.

Движение в пространстве и параллельный перенос.

Цели урока:

Познавательная: обобщение и систематизация знаний по теме «Геометрические преобразования в пространстве»; усвоение обучающимися знаний о симметрии, параллельном переносе и повороте в пространстве, преобразования симметрии, параллельного переноса и поворота в пространстве.
Воспитательная: пробуждение устойчивого интереса к предмету и активизации познавательной деятельности обучающихся; воспитание интереса к своей профессии;
Развивающая: развитие любознательности учащихся, познавательного интереса; развитие памяти; развитие способности обобщать. 
Задачи: формировать интерес к изучаемой дисциплине, развивать общеинтеллектуальные умения: сравнение, анализ, обобщение.

Тип урока: урок усвоения новых знаний.

Методы обучения: словесный, наглядный

Формы обучения: фронтальная, индивидуальная

Литература: Геометрия 10-11 кл. Анатасян

Ход урока:

1. Организационный момент.

Включает в себя приветствие учителем класса, подготовку помещения к уроку, проверку отсутствующих.

2. Проверка домашней работы.

3. Постановка цели урока.

Сегодня мы познакомимся с новой темой урока «Геометрические преобразования пространства».

4. Актуализация опорных знаний.

Проводится в форме фронтальной работы с классом.

• Какие преобразования плоскости вы знаете?

• Какое преобразование плоскости называется подобием? (преобразованием плоскости, при котором расстояния между точками умножаются на одно и то же положительное число).

• Сформулируйте свойства подобия. ( Подобие переводит отрезки в отрезки, лучи в лучи и прямые в прямые; Подобие сохраняет величину углов).

• Приведите примеры фигур, которые подобны себе при любом коэффициенте подобия. (Прямая, луч, полуплоскость, угол).

• Верно ли, что любые две окружности подобны? (Да)

5 . Изучение нового материала.

1) В алгебре рассматриваются различные функции. Функция каждому числу из области определения функции ставит в соответствие некоторое число – значение функции в точке . В геометрии рассматриваются функции, у которых другие области определения и множества значений. Они каждой точке ставят в соответствие точку. Эти функции называются геометрическими преобразованиями.

Геометрические преобразования имеют большое значение в геометрии. С помощью геометрических преобразований определяются такие важные геометрические понятия, как равенство и подобие фигур. Благодаря геометрическим преобразованиям, многие разрозненные факты геометрии укладываются в стройную теорию.

Для начала обратимся к некоторым основным понятиям, которые будут необходимы нам для работы с преобразованиями. Остановимся на двух терминах: расстояние и преобразование. Итак, что мы будем понимать под этими словами:

Определение. Расстоянием между двумя точками будем называть длину отрезка с концами в этих точках.

Определение. Преобразованием пространства называется взаимно-однозначное отображение пространства на себя.

Из этого определения следует важный вывод: при любом преобразовании пространства образы любых двух различных точек пространства различны и любые две различные точки пространства являются образами двух его различных точек.

Теперь перейдём к рассмотрению отдельных видов геометрических преобразований.

Центральная симметрия:

Введем определение центральной симметрии.

Преобразование пространства, при котором каждая точка пространства отображается на точку, симметричную ей относительно точки , называется центральной симметрией пространства относительно точки . При этом точка  отображается на себя и называется центром симметрии.

Примерами центральной симметрии являются: автомобильное колесо, окружность, куб, шар, снежинка, цветок и тд.

Движения в пространстве.

Симметрия относительно плоскости (зеркальная симметрия):

Определение. Преобразование пространства, при котором сохраняются расстояния между любыми двумя точками, называется движением пространства.

Свойства: при движении в пространстве прямые переходят в прямые, полупрямые – в полупрямые, отрезки – в отрезки, плоскости – в плоскости; сохраняются углы между полупрямыми.

Две фигуры называются равными, если они совмещаются движением.

В качестве примера движения пространства на данном этапе изучения стереометрии можно привести преобразование центральной симметрии, доказав координатным способом, что при этой симметрии сохраняются расстояния между точками.

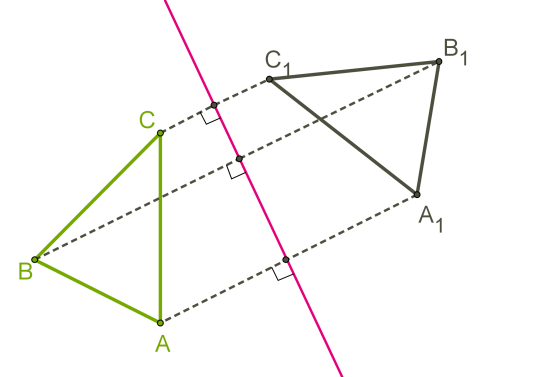
Введем понятие симметрии относительно плоскости:

Определение. Преобразование пространства, при котором каждая точка пространства отображается на точку, симметричную ей относительно плоскости , называется симметрией пространства относительно плоскости . Плоскость называется плоскостью симметрии.

Примеры симметрии относительно плоскости:

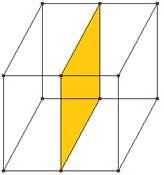
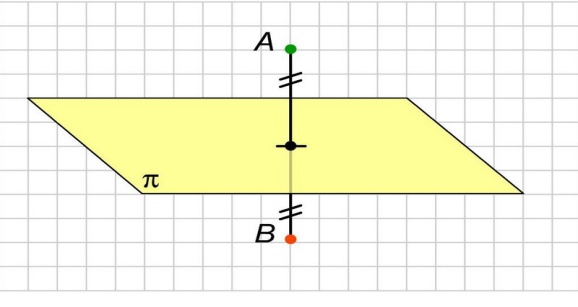
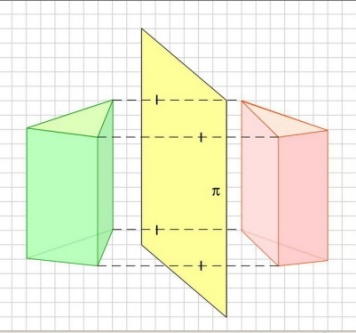
Параллельный перенос:

Определение. Параллельным переносом на вектор называется такое преобразование пространства, при котором любая точка  отображается на такую точку , что выполняется векторное равенство  . Это перенос (движение) всех точек пространства в одном и том же направлении, на одно и то же расстояние

Если плоскость (прямая) не параллельна вектору переноса, то при переносе на этот вектор она отображается на параллельную ей плоскость (прямую).

Примеры параллельного переноса:

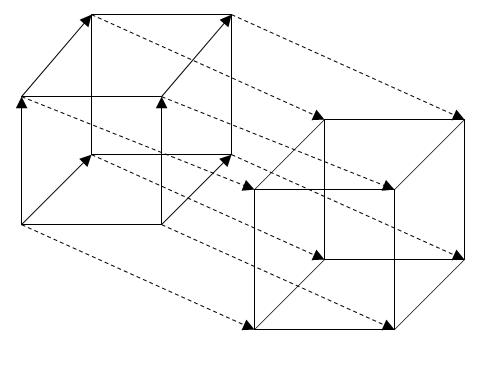
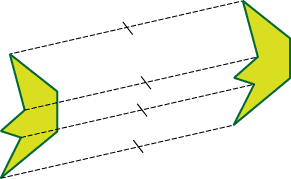
Осевая симметрия:

Определение. Осевая симметрия — это симметрия относительно проведённой прямой (оси).

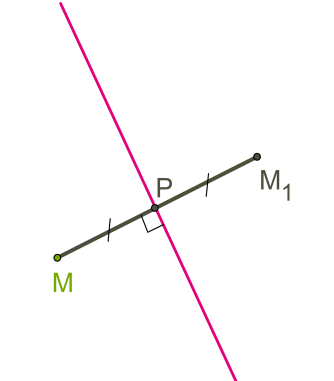
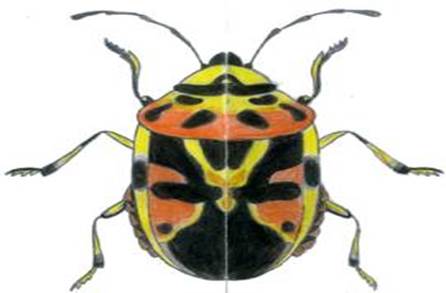
2) Решение примеров на доске:

Задача 1. Можно ли взаимно-однозначно отобразить: а) поверхность куба на поверхность другого куба; б) поверхность куба на сферу; Сделайте соответствующие рисунки.

Решение. а) Достаточно кубы расположить так, чтобы совпали их центры, а грани одного были параллельны граням другого. Тогда поверхность одного куба взаимно-однозначно отображается на поверхность другого куба посредством центрального проектирования из их общего центра. (Аналогичная задача планиметрии — о взаимно-однозначном отображении одного квадрата на другой посредством центрального проектирования.)

б) Достаточно центр сферы совместить с центром куба, тогда поверхность куба взаимно-однозначно отображается на сферу посредством центрального проектирования из их общего центра. (Аналогичная задача планиметрии — о взаимно-однозначном отображении квадрата — замкнутой ломаной — на окружность посредством центрального проектирования.)

6. Закрепление изученного материала.

Учитель: Решаем задания № 276, 277 , 278 (Атанасян Л.С. «Геометрия» 10-11 класс).

7. Домашнее задание.

Запись на доске и в дневниках: Принесите рисунки геометрических преобразований пространства.

8. Подведение итогов.

Учитель: Что нового вы узнали сегодня на уроке?