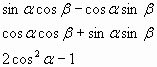Муниципальное Бюджетное Общеобразовательное Учреждение
«Школа 1538»
Конспект урока по алгебре и началам анализа "Преобразование тригонометрических выражений" (10 класс)
Иманова Л.А.
учитель математики
Москва
2024
Цели урока:
-
Систематизировать и обобщить знания о тригонометрических выражениях, опираясь на числовые окружности;
-
Развивать вычислительные навыки, творческое мышление, оригинальность мышления; развивать умения критически анализировать ситуации, навыки самоконтроля; создавать для учащихся ситуации критической самооценки.
-
подготовка к ЕГЭ.
Оборудование:1) набор перфокарт для индивидуальной работы.
Ход урока
-
Оргмомент. II.Сообщение темы и цели урока. Тема нашего урока “Преобразование тригонометрических выражений”.
Задача:обобщить и систематизировать материал по данной теме и выявить основные недочеты и трудности, над которыми надо еще поработать.
Девиз урока: ”Не берись за новое, не усвоив предыдущего”.
Обращаю ваше внимание, ребята на то, что все факты, связанные с тригонометрией не нужно запоминать наизусть, а достаточно понимать, где искать их на числовой окружности. Это и основное тригонометрическое тождество: sin? a +cos?a=1. (и все производные формулы), это и знаки тригонометрических функций по четвертям, все основные значения тригонометрических функций, это и решения всех простых уравнений.
III. Блиц-опрос по индивидуальным перфокартам.
Цель: проверка умений работать устно по единичной окружности.
| 1) sin 0 | 5) arctg1 | 9) 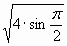 |
| 2) arccos 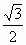 | 6) arcsin 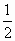 | 10) arcctg(-1) |
| 3) cos 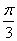 | 7) sin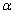 0, cos 0, cos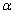 | 11) sin(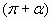 |
| 4) 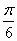 | 8) arccos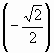
|
|
| | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 30 | | | | Х | | | | | | | |
| 2 | | | | | | | | | Х |
| |
| 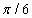
| | Х | | | | | | | | | |
| 0 | Х | | | | | | | | | | |
| 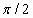
| | | Х | | | | | | | | |
| 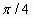
| | | | | Х | | | | | | |
| II | | | | | | | Х | | | | |
| 3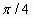 | | | | | | | | Х | | Х | |
| -sin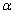 | | | | | | | | | | | Х |
Анализ работы. Результаты блиц – опроса ребята отмечают в листе учёта.
IV. Tест на проверку вычислительных навыков (индивидуальный)
Двое учащихся решают с обратной стороны доски для дальнейшей быстрой проверки.
| I вариант | II вариант |
| А1. Вычислите: 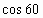 0+2sin300 + 0+2sin300 + 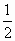 tg 2 600-ctg 450 tg 2 600-ctg 450 1) 1 2) -1 3) -2 4) 2 | А1. Вычислите: sin 2 450 + cos 600 + ctg 2 300 1) 3 2) 4 3) – 4 4) 2 |
| A2. Вычислите: 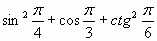 1) 4 2) 3 3) 2 4) 1 | А2. Вычислите: 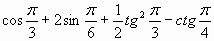 1) 1 2) 3 3) 2 4) -2 |
| А3. Найдите значение выражения: 14sin 2 x – 3, если cos 2 x= 0, 7 1) 2, 2 2) -1, 2 3) 1, 2 4) -2, 2 | А3. Вычислите cosx, если sinx = 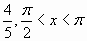 1) -0, 6 2) -0, 5 3) 0, 6 4) 1, 5 |
| А4. Вычислите: sin 75 0 1) v2 2) 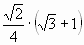 3) v3 4) 3) v3 4) 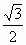 | А4. Вычислите: 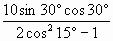 1) 6 2) 8 3) 4 4) 5 |
| В1. Вычислите: 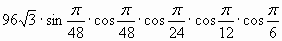 | В1. Вычислите: 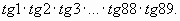
|
Анализ работы по тестам. Результаты ребята отмечают в листах учёта. Задаю вопросы: какие задания вызвали особые трудности, какой материал необходим для того , чтобы хорошо научиться решать эти задания, что особенно понравилось.
V. Pазвивающие задания.
3) Развивающий канон – это элемент интеллектуальной игры, составленный из шести элементов, связанных между собой логическими связями. Например,
| 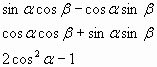
| - сos (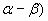 |
2) Проанализируйте следующие последовательности, выявите закономерность и продолжите запись:
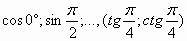 .
.
3) Известно, что 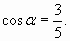 Найдите
Найдите 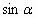 . Проанализируйте задание. Хватает ли данных в условии задачи?
. Проанализируйте задание. Хватает ли данных в условии задачи?
| 4) Развивающий канон: | 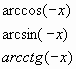
| - - arcsin x |
| аrcsin a = x - x Є [ 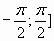 |
|
| аrccos a = x - x Є [ 0;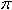 ] ] |
|
| аrcctg a = x - ? | Ответ: (0;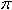 ) ) |
5) Работа в группах. Учащимся предлагаются карточки. Свободный выбор.
-
карточка “консультант” -ребята решают по образцу;
-
карточки для самостоятельного решения (часть “А”) ;
-
карточки для самостоятельного решения (часть “В” и часть “С”)
| А5. Вычислите 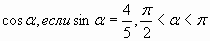 |
|
| А6. Вычислите 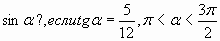 |
|
| А7. Найдите 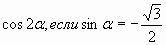 |
|
| В2. Найдите 50 sin 2x, если cos x = - 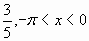 |
|
| А8. Упростите выражение: 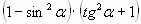 |
| А9. Упростите выражение: 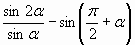 |
| А10. Упростите: 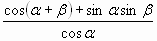 |
| А11. Вычислите: 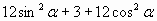 |
| В3. Найдите значение выражения 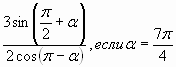 |
| В4. Найдите значение выражения 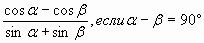 |
| В5. Вычислить sin 2x, если sinx+cosx=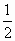 |
| В6. Вычислить ctg 3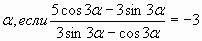 |
| В7. Вычислите 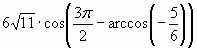 |
| В8. Вычислите 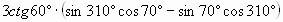 |
| В9. Вычислите  |
| В10. Вычислите 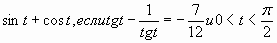 |
| C1. Вычислите 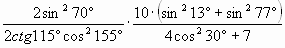 |
| В11. Вычислите 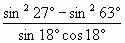 |
| С2. Вычислите 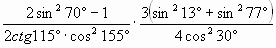 |
| С3. Найдите значение выражения: 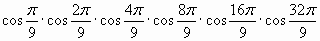
|
VI. Анализ работы в группах. Результаты отмечают ребята в листах учёта.
VI. Индивидуально- дифференцированная работа.
На “3”:
1) Упростите выражение: 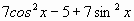
1) 1+ сos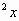 2) 2 3) -12 4) 12.
2) 2 3) -12 4) 12.
2) Вычислите 2 – tg ?x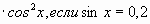
1) 1, 2 2) 1, 96 3) 1, 04 4) 1, 6
3) Вычислите cos x, если 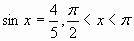
1) – 0, 6 2) 0, 6 3) 1, 6 4) – 1, 6.
На “4”:
4) Вычислите 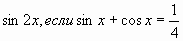 ;
;
5) Найдите значение выражения: 6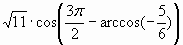
На “5”:
6) Вычислите: 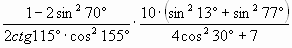
7) Дополнительные задания:
а) Какое общее название у объектов, входящих в эту группу?
у = sinx, y = cosx, y = tgx, y = ctgx. (Это тригонометрические функции).
б) Найдите лишнее: tgx, arcsinx, cosx, sinx. (arcsin x т. к – это обратная тригонометрическая функция)
в) Придумайте задание по тригонометрии для своего соседа по парте.
г) Вычислите 50sin2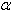 , если cos
, если cos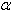 =
= 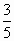 ,
, 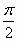
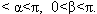 . Посмотрите нет ли лишних данных в условии задачи?
. Посмотрите нет ли лишних данных в условии задачи?
8) В конце урока каждый учащийся проводит самодиагностику с использованием кодификатора Нужно отметить в таблице своё отношение:
* -в повторении не нуждаюсь, знаю хорошо;
** - нужно напомнить на следующем уроке способ деятельности(алгоритм), еще раз обсудить;
*** - трудно, хочу решить подобную задачу в классе.
| Задания | * | ** | *** |
| 1) Нахождение значений тригонометрических выражений: 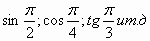
| | | |
| 2) Преобразование тригонометричеcких выражений: 5sin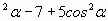 ; ; 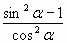 и т. д. и т. д.
| | | |
| 3) Для преобразования выражений использую формулы: а) основное тригонометрическое тождество: 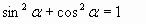
б) произведение тангенса и котангенса одного и того же аргумента: tgx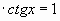 ; ; в) зависимость между тангенсом и косинусом одного и того же аргумента: 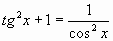 ; ;
г) зависимость между ctgx и sinx: 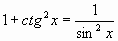 . .
| | | |
| 4) Использую формулы сложения: а) синус суммы: sin(x+y) =sinx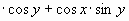 ; ; б) синус разности: 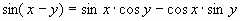
в) косинус суммы: 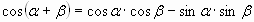
г) косинус разности: 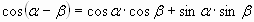
| | | |
| 5) Использую следствия из формул сложения: а) sin 2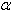 = 2sin = 2sin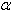 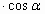 ; ; б) cos2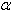 =cos2 =cos2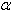 -sin2 -sin2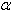 = = 1-2sin2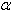 =2cos2 =2cos2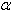 -1; -1; в) 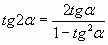 | | | |
| | | | |
Подведение итогов по листам учёта.
Учащиеся сами оценивают.
Лист учёта
Фамилия, имя _____________________________________________________________
| Этапы | Кто оценивает | наибольшее кол-во баллов |
| 1. Блиц опрос. | Взаимопроверка в парах. | 11 |
| 2. Вводный тест. | самооценка | 5 |
| 3. Работа в группах: а) часть “А” б) часть “В” в) часть “С” | консультант | 1 2 3 |
| 4. Индивидуально-дифференцированная работа: а) на “3” б) на “4” в) на “5” | учитель | 3 4 5 |
| 5. Дополнительные задания. | учитель | 1 |
| 6. Работа в классе по развивающим заданиям. | учитель | 1 |
| 7. Итого | | |
| 8. Оценка. | | |
| Критерии оценок: На “5”- 33-36 баллов; На “4”- 20- 32 баллов; На “3”- 12-19 баллов. |
|
|
IX. Рефлексия.
“Сегодня на уроке математики…”, “Мне понравилось…”, “Хочу предложить …”.
Ваши ассоциации при изучении темы “Преобразование тригонометрических выражений ”.
Терпение
Радость
Интересно
Г
Окружность
Нравится
О
М
ЕГЭ
Трудолюбие
Реально
И
Ясно