Превращение энергии при колебательном движении.

Рассмотрим превращения энергии при колебаниях математического маятника.

Выберем систему отсчёта таким образом, чтобы в положении равновесия его потенциальная энергия была равна нулю.

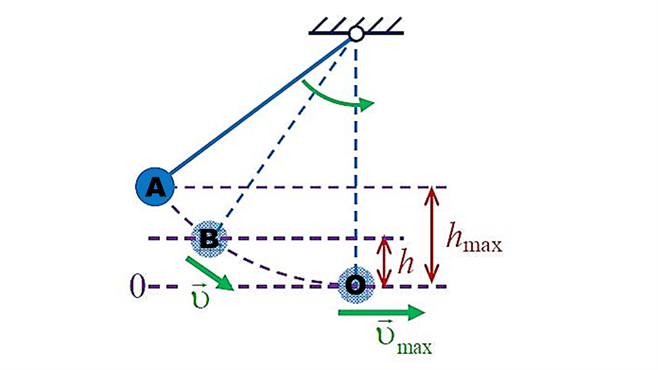
При колебаниях математического маятника изменяется высота h грузика относительно положения равновесия и изменяется его скорость υ.

Причём при максимальных смещениях высота достигает максимального значения hmax, а скорость становится равной нулю, в положении равновесия — наоборот: высота тела равна нулю, а скорость достигает максимального значения vmax.

Так как высота тела определяет его потенциальную энергию

Eп=mgh,

а скорость — кинетическую энергию

Eк=mv22,

то вместе с изменением высоты и скорости будут изменяться и энергии.

Когда маятник находится в точке, где его смещение от положения равновесия максимально (крайняя левая (или крайняя правая) точка траектории его движения — точка A), то кинетическая энергия маятника равна минимально возможному значению — нулю:

Eкmin=0,

а потенциальная энергия максимальна и равна:

Eпmax=mghmax.

Таким образом, полная механическая энергия маятника в крайних левой и правой точках равна:

E1=Eпmax+Eкmin=mghmax.

Когда маятник находится в какой-либо промежуточной точке между крайней левой или правой точками (точками, где смещение маятника от положения равновесия максимально) и положением равновесия (точка B), то его полная механическая энергия E равна:

E2=Eп+Eк=mgh+mv22.

При этом потенциальная и кинетическая энергии принимают некоторые промежуточные значения, большие 0 и меньшие максимального значения:

Eп=mgh,

Eк=mv22.

Когда маятник проходит положение равновесия (точка O), то его кинетическая энергия максимальна и равна

Eкmax=mv2max2,

а потенциальная энергия принимает нулевое значение

Eпmin=0.

Тогда полная механическая энергия в точке равновесия равна:

E3=Eпmin+Eкmax,

E3=0+mv2max2=mv2max2.

Таким образом можно составить цепочку превращений одного вида энергии в другой при движении математического маятника от крайней левой точки до положения равновесия:

точка A→ точка B→ точка O,

Eпmax→Eп+Eк→Eкmax,

mghmax→mgh+mv22→mv2max2.

При движении математического маятника от положения равновесия до крайней правой точки происходит обратное превращение энергии: кинетическая энергия уменьшается от своего максимального значения до нуля, а потенциальная увеличивается от нуля до своего максимального значения.

Обрати внимание!

Полная механическая энергия математического маятника в любой точке траектории его движения постоянна.