Презентации задач огэ

Задания огэ. №9

Выполнила: Хасанова Лидия

9а класс

№ 9 ( Вариант 1)

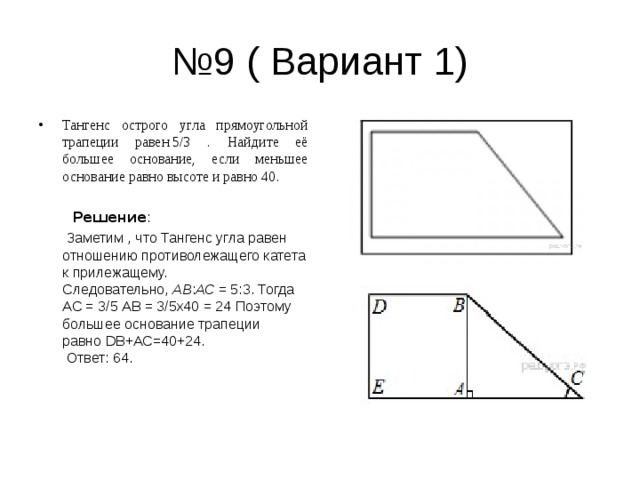
• Тангенс острого угла прямоугольной трапеции равен 5/3 . Найдите её большее основание, если меньшее основание равно высоте и равно 40.

Решение :

Заметим , что Тангенс угла равен отношению противолежащего катета к прилежащему. Следовательно,  АВ : АС  = 5:3. Тогда АС = 3/5 АВ = 3/5х40 = 24 Поэтому большее основание трапеции равно  D В+АС=40+24. Ответ: 64.

№ 9 ( Вариант 2)

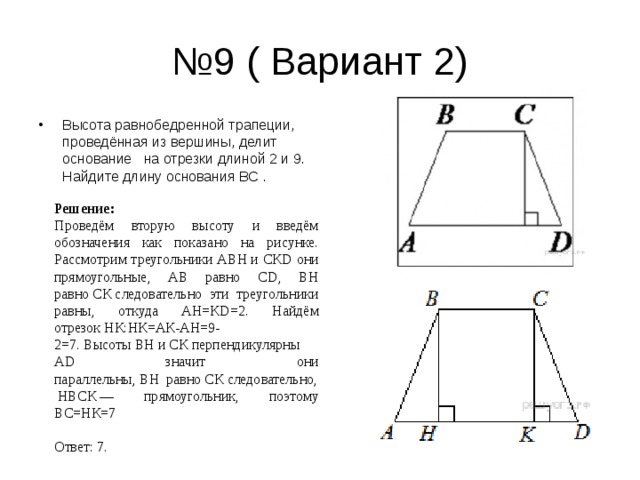
• Высота равнобедренной трапеции, проведённая из вершины, делит основание   на отрезки длиной 2 и 9. Найдите длину основания ВС .

Решение:

Проведём вторую высоту и введём обозначения как показано на рисунке. Рассмотрим треугольники АВН и СК D они прямоугольные, АВ равно С D , ВН равно СК следовательно эти треугольники равны, откуда АН=К D =2. Найдём отрезок НК:НК=АК-АН=9-2=7. Высоты ВН и СК перпендикулярны А D значит они параллельны, ВН  равно СК следовательно, НВСК — прямоугольник, поэтому ВС=НК=7           

Ответ: 7.

№ 9 ( Вариант 3)

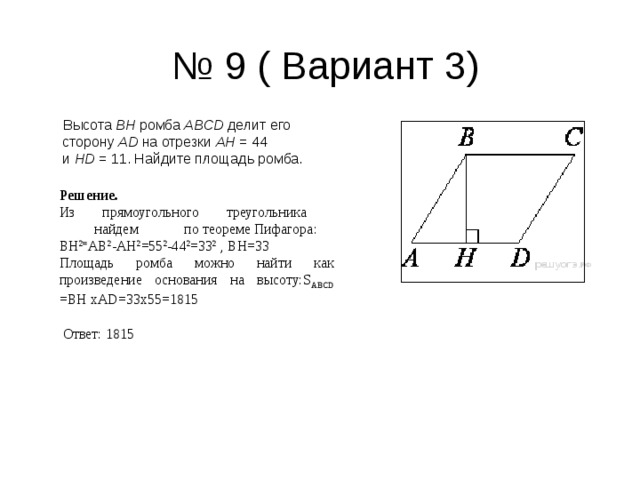
Высота  BH  ромба  ABCD  делит его сторону  AD  на отрезки  AH  = 44 и  HD  = 11. Найдите площадь ромба.

Решение.

Из прямоугольного треугольника           найдем            по теореме Пифагора:

ВН 2= АВ 2 -АН 2 =55 2 -44 2 =33 2 , ВН=33

Площадь ромба можно найти как произведение основания на высоту: S АВС D = ВН хА D =33х55=1815

Ответ: 1815

№ 9 ( Вариант 5)

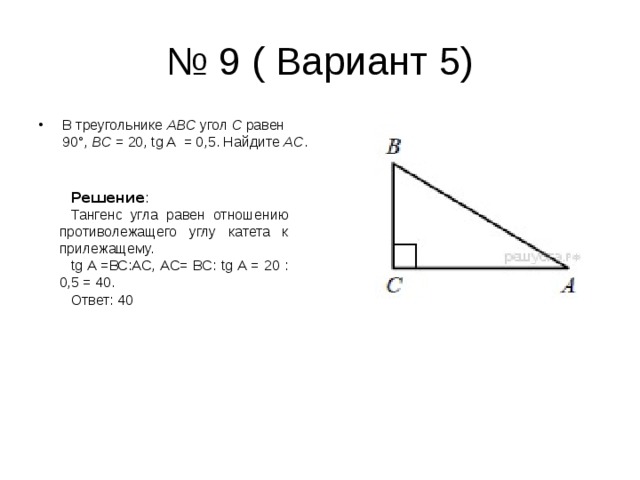
• В треугольнике  ABC  угол  C  равен 90°,  BC  = 20,  tg A  = 0,5. Найдите  AC .

Решение :

Тангенс угла равен отношению противолежащего углу катета к прилежащему.

tg A = ВС:АС, АС= ВС: tg A = 20 : 0,5 = 40.

Ответ: 40

№ 9 ( Вариант 6)

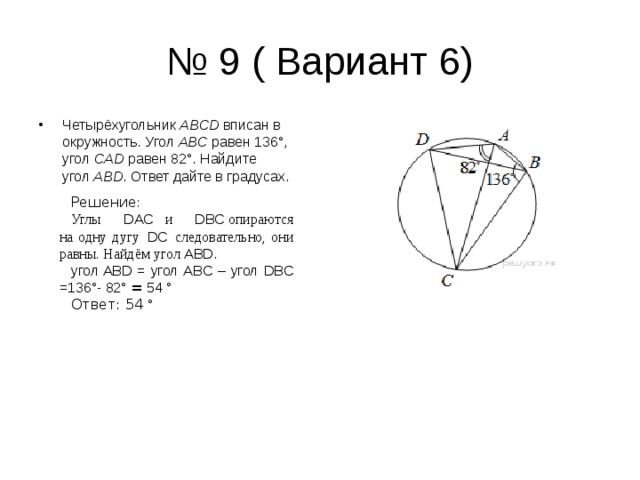
• Четырёхугольник  ABCD  вписан в окружность. Угол  ABC  равен 136°, угол  CAD  равен 82°. Найдите угол  ABD . Ответ дайте в градусах.

Решение :

Углы    DAC     и    DBC  опираются на одну дугу    DC    следовательно, они равны. Найдём угол   ABD .

угол ABD = угол ABC – угол DBC =136 ° - 82 ° = 54 °

Ответ: 54 °

№ 9 ( Вариант 7)

• Сумма двух углов равнобедренной трапеции равна 220°. Найдите меньший угол трапеции. Ответ дайте в градусах .
• Так как сумма односторонних углов трапеции равна 180°, в условии говорится о сумме углов при основании. Поскольку трапеция является равнобедренной, углы при основании равны. Значит, каждый из них равен 110°. Сумма односторонних углов трапеции равна 180°, поэтому меньший угол равен 180° − 110° = 70°.
•  
• Ответ: 70.

№ 9 ( Вариант 8)

• Высота равностороннего треугольника равна 12  . Найдите сторону этого треугольника.
• Решение.
• Высота равностороннего треугольника равна  :2,следовательно сторона треугольника х 2 : =24
• Ответ: 24

№ 9 ( Вариант 9)

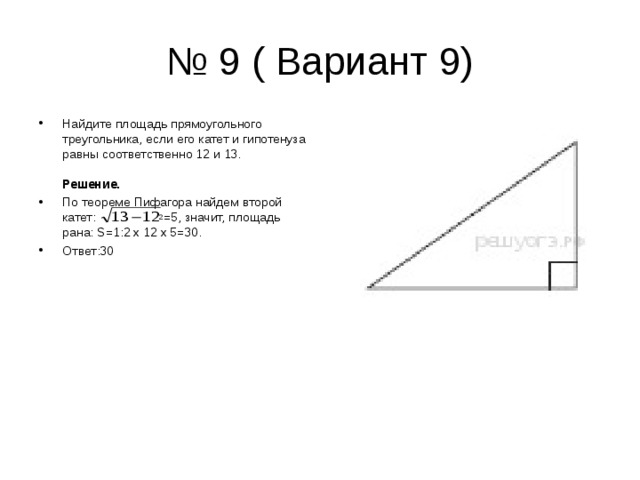
• Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 12 и 13. Решение.
• По теореме Пифагора найдем второй катет:  2 =5, значит, площадь рана: S= 1:2 х 12 х 5=30.
• Ответ:30

№ 9 ( Вариант 10)

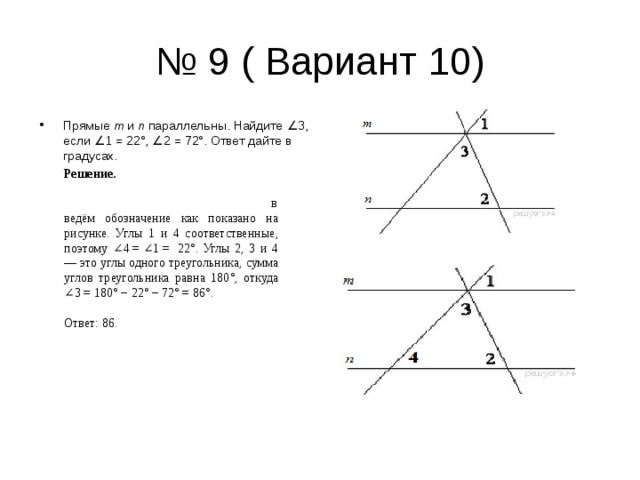
• Прямые  m  и  n  параллельны. Найдите ∠3, если ∠1 = 22°, ∠2 = 72°. Ответ дайте в градусах.

Решение.

                                                                    введём обозначение как показано на рисунке. Углы 1 и 4 соответственные, поэтому ∠4 = ∠1 =  22°. Углы 2, 3 и 4 — это углы одного треугольника, сумма углов треугольника равна 180°, откуда ∠3 = 180° − 22° − 72° = 86°.

Ответ: 86.

№ 9 ( Вариант 11)

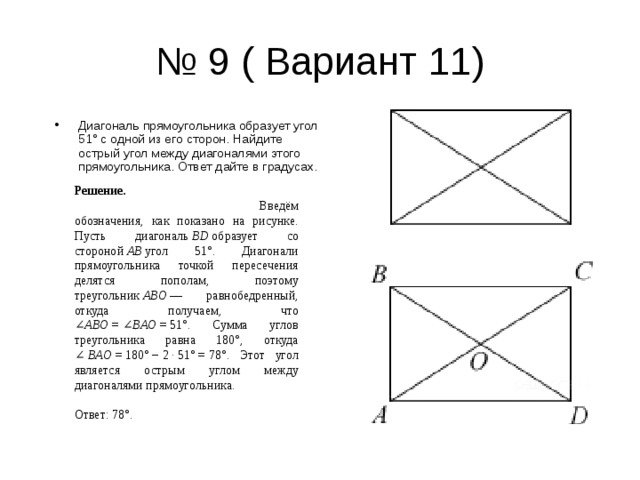
• Диагональ прямоугольника образует угол 51° с одной из его сторон. Найдите острый угол между диагоналями этого прямоугольника. Ответ дайте в градусах.

Решение.

                                    Введём обозначения, как показано на рисунке. Пусть диагональ  BD  образует со стороной  AB  угол 51°. Диагонали прямоугольника точкой пересечения делятся пополам, поэтому треугольник  ABO  — равнобедренный, откуда получаем, что ∠ ABO  = ∠ BAO  = 51°. Сумма углов треугольника равна 180°, откуда ∠  BAO  = 180° − 2 · 51° = 78°. Этот угол является острым углом между диагоналями прямоугольника.

Ответ: 78°.

№ 9 ( Вариант 12)

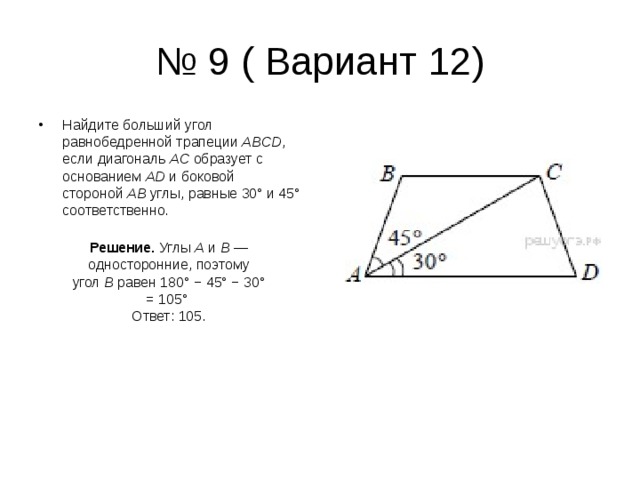
• Найдите больший угол равнобедренной трапеции  ABCD , если диагональ  AC  образует с основанием  AD  и боковой стороной  AB  углы, равные 30° и 45° соответственно.

Решение. Углы  А  и  В  — односторонние, поэтому угол  В  равен 180° − 45° − 30° = 105°

Ответ: 105.

№ 9 ( Вариант 13)

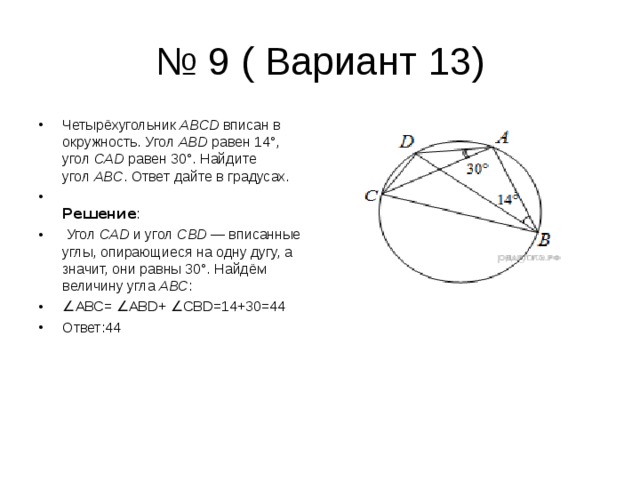
• Четырёхугольник  ABCD  вписан в окружность. Угол  ABD  равен 14°, угол  CAD  равен 30°. Найдите угол  ABC . Ответ дайте в градусах.
• Решение :
• Угол  CAD  и угол  CBD  — вписанные углы, опирающиеся на одну дугу, а значит, они равны 30°. Найдём величину угла  ABC :
• ∠ АВС= ∠АВ D + ∠ CBD =14+30=44
• Ответ:44

№ 9 ( Вариант 14)

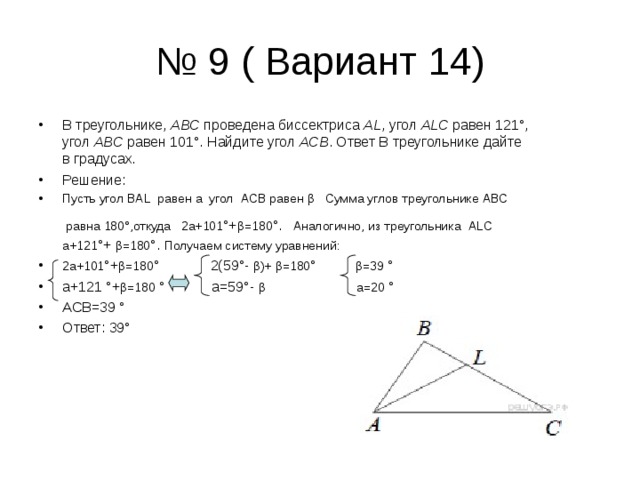
• В треугольнике,  ABC  проведена биссектриса  AL , угол  ALC  равен 121°, угол  ABC  равен 101°. Найдите угол  ACB . Ответ В треугольнике дайте в градусах.
• Решение:
• Пусть угол  BAL  равен а  угол  ACB  равен β    Сумма углов треугольнике  ABC  равна 180°,откуда  2а+101 °+ β =180 °.   Аналогично, из треугольника  ALC а+121 °+ β =180 °. Получаем систему уравнений:
• 2а+101 °+ β =180 ° 2(59°- β )+ β =180 ° β =39 °
• а+121 °+ β =180 ° а=59°- β а=20 °
• АСВ=39 °
• Ответ: 39°

№ 9 ( Вариант 15)

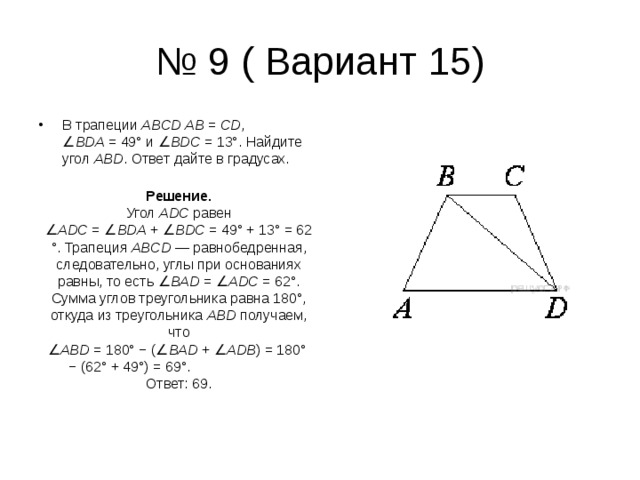
• В трапеции  ABCD   AB  =  CD , ∠ BDA  = 49° и ∠ BDC  = 13°. Найдите угол  ABD . Ответ дайте в градусах.

Решение.

Угол  ADC  равен ∠ ADC  = ∠ BDA  + ∠ BDC  = 49° + 13° = 62°. Трапеция  ABCD  — равнобедренная, следовательно, углы при основаниях равны, то есть ∠ BAD  = ∠ ADC  = 62°. Сумма углов треугольни­ка равна 180°, откуда из треугольника  ABD  получаем, что ∠ ABD  = 180° − (∠ BAD  + ∠ ADB ) = 180° − (62° + 49°) = 69°. Ответ: 69.