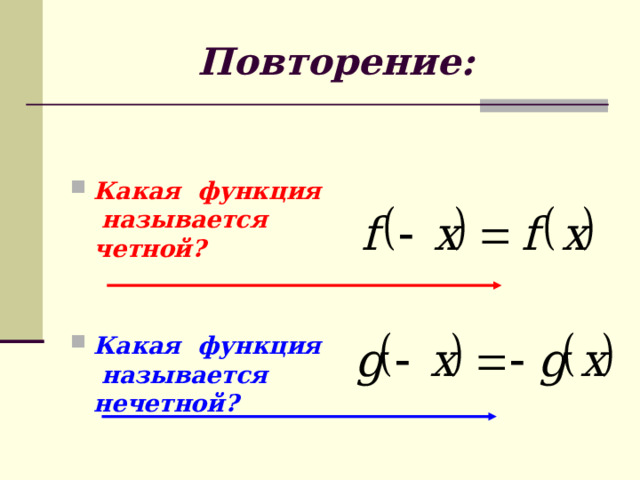
Презентация "Чётные и нечётные функции"

Четные и нечетные функции.

Повторение:

• Какая функция называется четной?

• Какая функция называется нечетной?

Повторение:

• Может ли быть четной или нечетной функция, областью определения которой является:

а) промежуток [ -2 ; 5 ]

г) объединение промежутков

[ -10 ; -2 ] и [ 2 ; 10 ]

б) промежуток ( -5; 5 )

в) промежуток ( -3; 3 ]

Повторение:

• Функция f (x) – четная,

f ( 3 ) = 25 , тогда f ( -3 ) = ?

f ( -8 ) = 71, тогда f ( 8 ) = ?

25

71

• Функция g ( x ) – нечетная,

g ( 7 ) = 43, тогда g ( -7 ) = ?

g ( - 2 ) = -64, тогда g ( 2 ) = ?

-43

64

Повторение:

• Ломаная АВС , где А ( 5; 1 ), В ( 3; 5 ),

С ( 0; 0 ) – часть графика некоторой функции f ( x ) . Область определения этой функции – промежуток [ -5 ; 5 ] .

Постройте ее график, зная, что:

I – f ( x ) – четная .

II – f ( x ) – нечетная.

№ 485 ( а, в )

№ 485 ( б, д )

Домашнее задание: №№ 515; 490; 492 ( б ).

Четные и нечетные функции. Математический диктант.

№ 1.

• Является ли функция четной или нечетной?

I вариант.

II вариант.

№ 2.

I вариант.

Каково свойство графика нечетной функции?

II вариант.

Каково свойство графика четной функции?

№ 3. Укажите графики функций I – четных. II – нечетных.