Презентация "Функции и их свойства"

Функции и их свойства

y

y = f( x )

x

0

• Определите вид функций.

Свойства функций:

периодичность

Говорят, что функция y = f(x) , х ∊ Х имеет период Т , если для любого х ∊ Х выполняется равенство

f(x – Т ) = f(x) = f(x + T) .

Функцию, имеющую отличный от нуля период называют периодической .

Если функция y = f(x) , х ∊ Х имеет период Т, то любое число, кратное Т (т.е. число вида kT , k ∊ Z ), также является ее периодом.

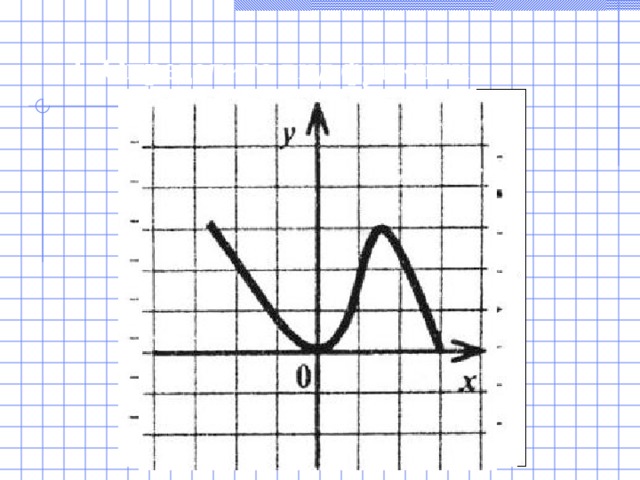
2. Дан фрагмент графика четной функции f(х), которая

определена на [–9; 9]. Достройте график функции f(х) и ответьте на следующие вопросы:

• Сколько нулей функции на этом промежутке?
• Сколько промежутков возрастания и убывания?
• Сколько промежутков, на которых значения функции

положительны (отрицательны)?

• Выполните это же задание, учитывая, что теперь дан

фрагмент нечетной функции. 

1. Периодическая функция y = f (x) определена для всех действительных чисел. Её период равен 4 и f (3) = 8. Найдите значение выражения

7 f(15) – 2f(-1) – 4f(-17).

2. Периодическая функция y = f (x) определена на всей числовой оси. Её период равен 3. На промежутке [-2;1) значения функции y = f (x) совпадают со значениями функции

Вычислите f (11).

3. Найдите значения функций

а)

y =

если известно, что функция y = f (x) - нечётная, функция y = g (x) – чётная, f (a) = 2, g (a) = -5.

в точке x ο , если известно, что

y = f (x) – чётная функция,

y = g (x) – нечётная функция,

f (x ο ) = 2,

g (x ο ) = 1.

4.

5. Найдите значение функции f (9) , если известно, что функция y = f (x) – чётная , имеет период 10 и на отрезке [0 ;5 ] функция имеет вид y = 15 + 2x - x 2

6. Четная функция y = f (x) определена на всей числовой прямой. Для всякого неотрицательного значения переменной x значение этой функции совпадает со значением функции g (x) = 13x(2x+1)(7x+6)(4x-9).

Сколько корней имеет уравнение f (x) =0 ?

7. Для чётной функции f (x) и нечётной функции g (x) для всех действительных значений аргумента выполнено равенство

f (x) + g (x) = 2x² - 7x - 5 .

Найдите корень (или сумму корней, если их несколько) уравнения f (x) = g (x).