© 2021, Ахметзянова Айнара Тюлегеновна 1164 68
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до 17.06.2025
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Был в сети 20.05.2025 14:36
Ахметзянова Айнара Тюлегеновна
МОАУ "Лицей №1 г. Оренбурга"
33 года
658
80 535 
Специализация
Презентация «Графический способ решения систем линейных уравнений с двумя переменными»
Категория:
Алгебра
17.03.2021 19:08
Учебник:
Алгебра. 7 класс. Учебник. Макарычев Ю.Н., Миндюк Н.Г. и др. 13-е изд., стер. - М.: 2013. - 336 с.
Просмотр содержимого документа
«Презентация «Графический способ решения систем линейных уравнений с двумя переменными»»
Урок по алгебре
7 класс
25 апреля 2018 г
Устный счет
1. Является ли пара чисел (2;-5) решением уравнения:
Что такое линейное уравнение?
А) 2х+у=9;
Сколько решений имеет линейное уравнение с двумя переменными?
Б) х-у=7;
В) -х+у=3;
Г) у-2х=-9?
Выразите переменную у через х из уравнения:
х+у=1
у=1-х
3х-у=2
у=3х-2
А сколько может быть уравнений в системе?
Что является решением системы уравнений?
Проверка домашнего задания
№ 1057
№ 1058
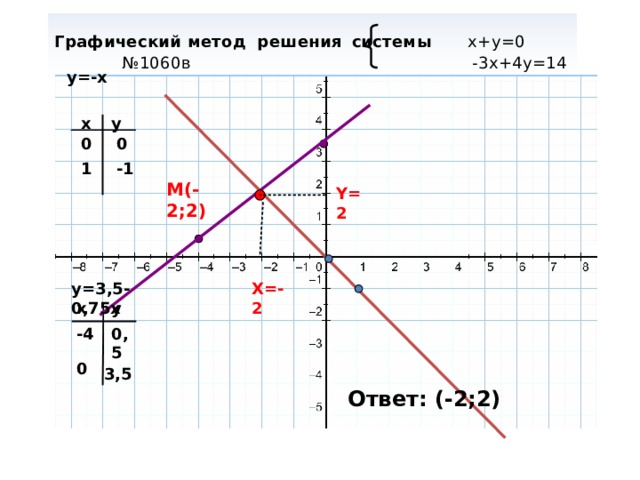
Графический метод решения системы х+у=0 №1060в -3х+4у=14
у=-x
x
y
0
0
1
-1
M(-2;2)
Y=2
X=-2
у=3,5-0,75х
y
x
0,5
-4
0
3,5
Ответ: (-2;2)
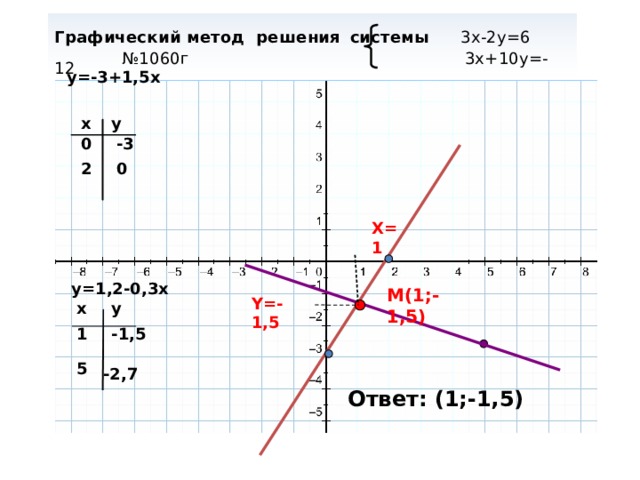
Графический метод решения системы 3х-2у=6 №1060г 3х+10у=-12
у=-3+1,5х
x
y
0
-3
0
2
X=1
у=1,2-0,3х
M(1;-1,5)
Y=-1,5
x
y
1
-1,5
5
-2,7
Ответ: (1;-1,5)
Алгоритм решения системы уравнений графическим способом
1. Выразить из каждого уравнения переменную у через х.
2. Построить график каждого уравнения
3. Найти общее решение этих уравнений.
4. Записать ответ.
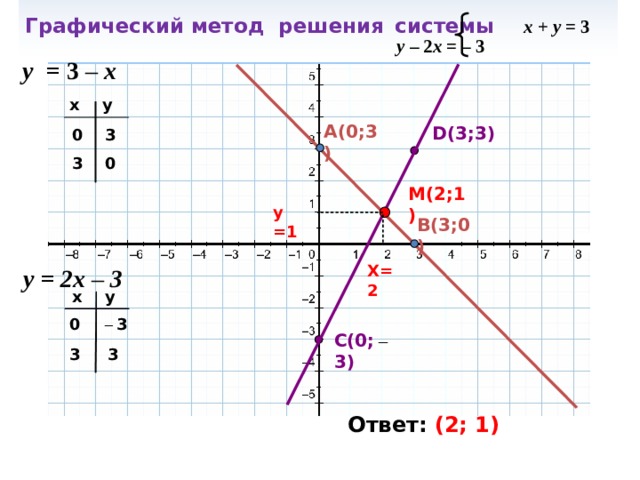
Графический метод решения системы x + y = 3 y – 2 x = – 3
у = 3 – x
x
y
A(0;3)
D(3;3)
3
0
0
3
M(2;1)
у =1
B(3;0)
X=2
у = 2x – 3
y
x
0
– 3
C(0; – 3)
3
3
Ответ: (2; 1)
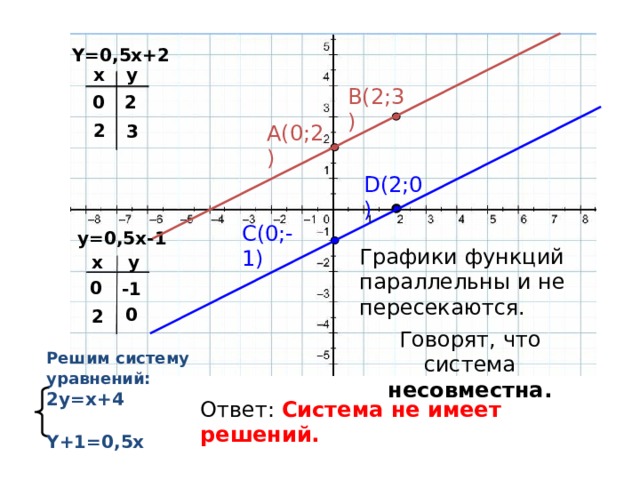
Y=0,5x+2
x
y
B(2;3)
0
2
2
A(0;2)
3
D(2;0)
C(0;-1)
y=0,5x-1
Графики функций параллельны и не пересекаются.
y
x
0
-1
0
2
Говорят, что система несовместна.
Решим систему уравнений: 2y=x+4 Y+1=0,5x
Ответ: Система не имеет решений.
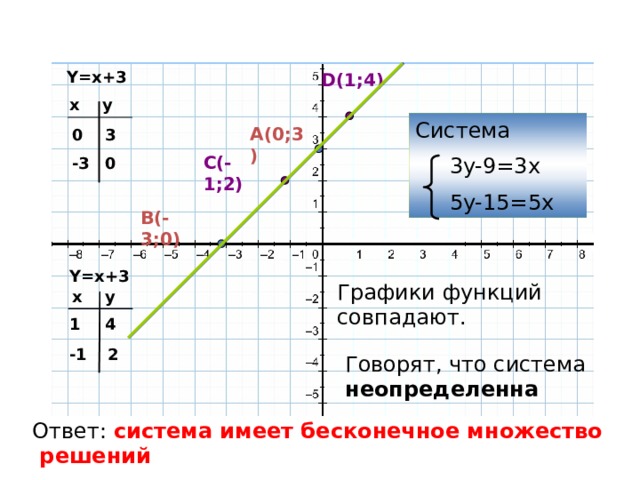
Y=x+3
D(1;4)
y
x
Система
3y-9=3x
5y-15=5x
A(0;3)
0
3
C(-1;2)
0
-3
B(-3;0)
Y=x+3
Графики функций совпадают.
y
x
4
1
2
-1
Говорят, что система неопределенна
Ответ: система имеет бесконечное множество решений
Если система уравнений имеет решений, то она называется совместной. Если система уравнений не имеет решений, то она называется несовместной. Если система уравнений имеет бесконечно много решений, то она называется неопределённой.
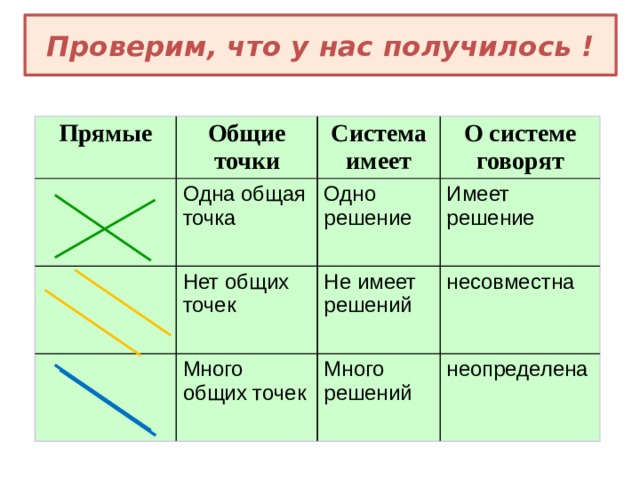
Проверим, что у нас получилось !
Прямые
Общие точки
Одна общая точка
Система имеет
Нет общих точек
Одно решение
О системе говорят
Имеет решение
Много общих точек
Не имеет решений
Много решений
несовместна
неопределена
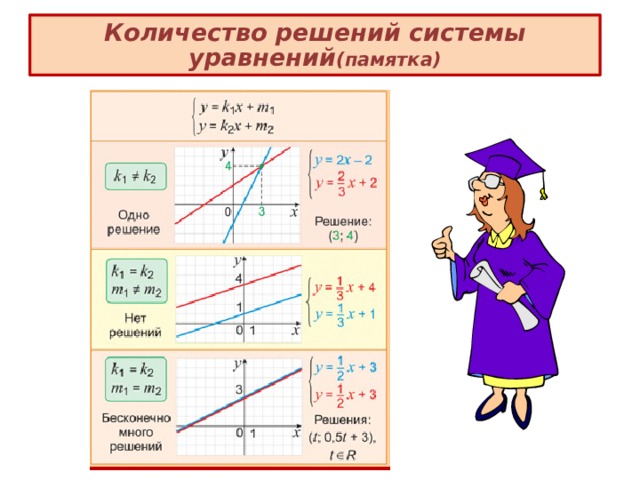
Количество решений системы уравнений (памятка)
С п а с и б о за у р о к
Достоинство графического способа – наглядность.
Недостаток графического способа– приближённые значения переменных.
Домашнее задание
1)теория на странице 207-208, выучить определения, ответить на вопросы после пункта.
2)Письменно выполнить номера из учебника: №1061б, 1062бвд, 1063б.
3) Дополнительное задание*: подберите, если возможно, такое значение k, при котором данная система имеет единственное решение, не имеет решений, имеет бесконечное множество решений.
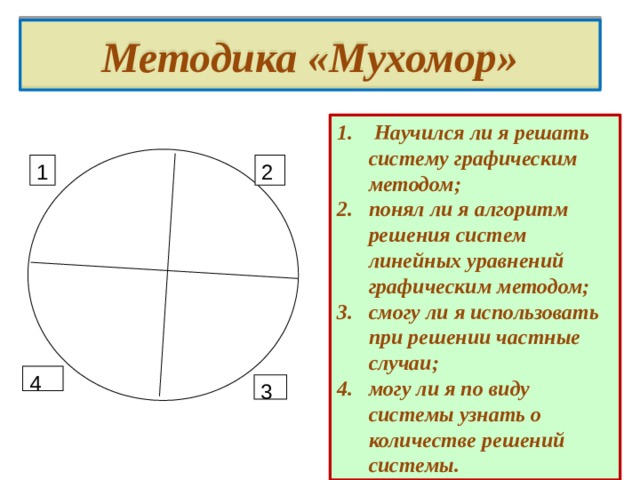
Методика «Мухомор»
- Научился ли я решать систему графическим методом;
- понял ли я алгоритм решения систем линейных уравнений графическим методом;
- смогу ли я использовать при решении частные случаи;
- могу ли я по виду системы узнать о количестве решений системы.
1
2
4
3
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
Полезное для учителя
Реализация образовательных программ осуществляется с применением исключительно электронного обучения и ДОТ
