Презентация к уроку по теме: Решение систем линейных уравнений с двумя переменными. ( 8 класс)

ПРИМЕРЫ:

• 4х 2 +3х+5=0
• 3х+2y=6
• 4х+9у=7
• 9( х 2 +6х+2)-8=30
• x 2 /3+y 2 /2=1

• 4(х+2)+1=y+18

Назови линейные уравнения с двумя переменными.

ПРИМЕРЫ:

• 4х 2 +3х+5=0
• 3х+2y=6
• 4х+9у=7
• 9( х 2 +6х+2)-8=30
• x 2 /3+y 2 /2=1

• 4(х+2)+1=y+18

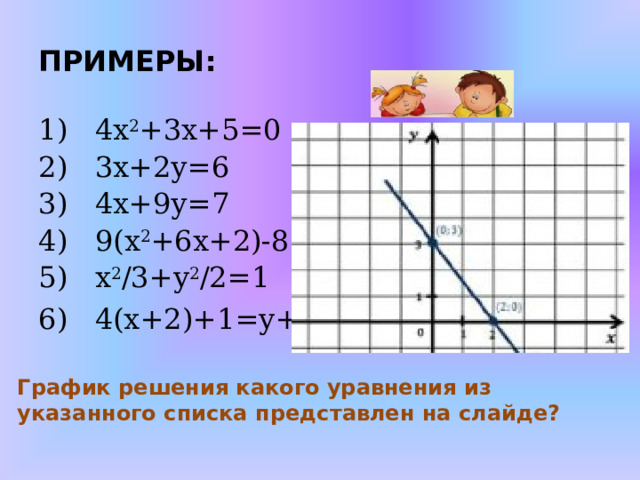
ПРИМЕРЫ:

• 4х 2 +3х+5=0
• 3х+2у=6
• 4х+9у=7
• 9( х 2 +6х+2)-8=30
• x 2 /3+y 2 /2=1

• 4(х+2)+1=y+18

График решения какого уравнения из указанного списка представлен на слайде?

Решение систем двух линейных уравнений с двумя переменными

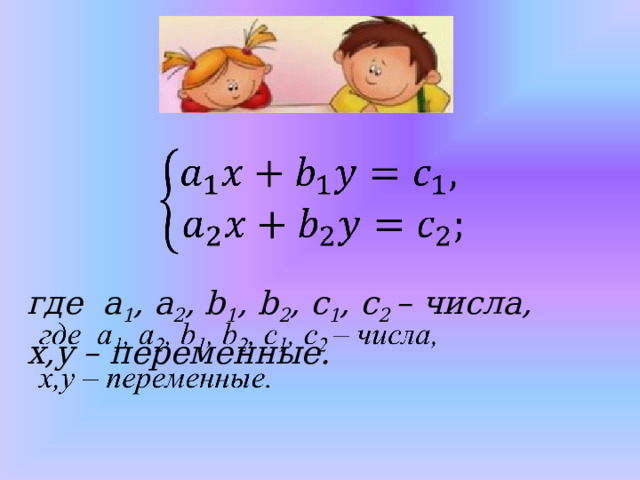
где a 1 , a 2 , b 1 , b 2 , c 1 , c 2 – числа, x,y – переменные.

Цель:

формирование представления о системах линейных уравнений с двумя переменными и способах их решений.

Задачи:

• познакомиться с аналитическим и графическим способом решения систем линейных уравнений с двумя переменными;
• сформировать первичное представление о способах решения систем линейных уравнений с двумя переменными.

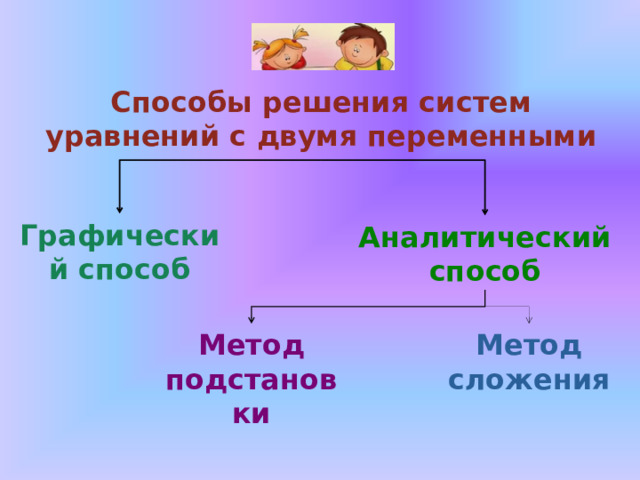
Способы решения систем уравнений с двумя переменными

Графический способ

Аналитический способ

Метод подстановки

Метод сложения

Графический способ

В одной координатной плоскости строим графики двух линейных уравнений (прямые).

• если графики пересекаются в одной точке - система имеет единственное решение (точка пересечения графиков);
• если графики параллельны — система не имеет решения (система несовместна);
• если графики совпадают — система имеет бесконечно много решений (система неопределенна).

Пример:

Решить графическим способом систему линейных уравнений с двумя переменными:

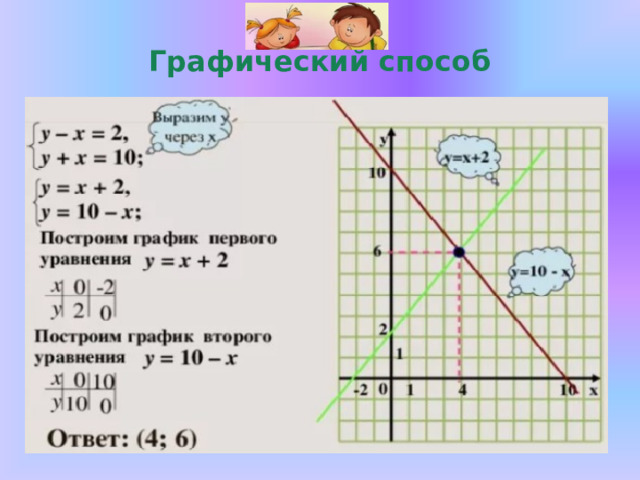
Графический способ

Аналитический способ

Метод подстановки:

• из более простого уравнения выразить одно неизвестное через другое;
• подставить полученное выражение в другое уравнение выраженной переменной;
• решить полученное уравнение с одной переменной;
• подставить найденное значение переменной в уравнение, полученное на 1 шаге. Найти вторую переменную;
• записать ответ.

Пример:

Решить методом подстановки систему линейных уравнений с двумя переменными:

Аналитический способ

Метод подстановки:

Пример:

Решить методом подстановки систему линейных уравнений с двумя переменными:

Ответ: (4;6)

Аналитический способ

Метод сложения:

• подобрав «выгодные» множители, преобразовать одно или оба уравнения системы так, чтобы коэффициенты при одной из переменных стали противоположными числами;
• сложить почленно левые и правые части полученных уравнений;
• решить уравнение с одной переменной;
• подставить найденное значение переменной в любое из уравнений исходной системы;
• вычислить значение другой переменной;
• записать ответ.

Пример:

Решить методом сложения систему линейных уравнений с двумя переменными:

Аналитический способ

Метод сложения:

Пример:

Решить методом сложения систему линейных уравнений с двумя переменными:

Ответ: (4;6)

Способы решения систем уравнений с двумя переменными

Графический способ

Аналитический способ

Метод подстановки

Метод сложения

Самостоятельная работа

Дополнительно:

Спасибо за работу!

Домашнее задание: 1. Повторить записи в тетради 2. Выполнить задание на Якласс: https://www.yaklass.ru/TestWork/CopyShared/MgFY-oYn2EyAbK-yfW0dSw

ИСПОЛЬЗУЕМАЯ ЛИТЕРАТУРА

• Учебник «Алгебра 7», «Алгебра 9». Авторы: Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова; под ред. С.А. Теляковского. Линия УМК, серия Алгебра. Макарычев Ю.Н. (7-9) , Москва «Просвещение», 2024
• Яндекс-картинки: https://yandex.ru/images/search?from=tabbar&img_url=https%3A%2F%2Ffs.znanio.ru%2Fd5af0e%2F74%2F66%2F8872d379aa01d7e445ecd636bd4494e933.jpg