
9 класс АЛГЕБРА
Квадратные неравенства и их решение.
Подготовил: Попов Дмитрий Сергеевич

На сегодняшнем уроке мы с вами рассмотрим определение квадратных неравенств и научимся решать их.
 0, где а ≠ 0, называют квадратным неравенством. Примечание к определению: вместо знака могут стоять и другие знаки неравенства: " width="640"
0, где а ≠ 0, называют квадратным неравенством. Примечание к определению: вместо знака могут стоять и другие знаки неравенства: " width="640"
Что такое квадратное неравенство?
Неравенство вида а х 2 + b х + с 0, где а ≠ 0, называют квадратным неравенством.
Примечание к определению: вместо знака могут стоять и другие знаки неравенства:
 3 график расположен выше оси х , т. е. значения функции положительны. Иными словами, неравенство х 2 – 2х – 3 0 выполняется при х и х 3. " width="640"
3 график расположен выше оси х , т. е. значения функции положительны. Иными словами, неравенство х 2 – 2х – 3 0 выполняется при х и х 3. " width="640"
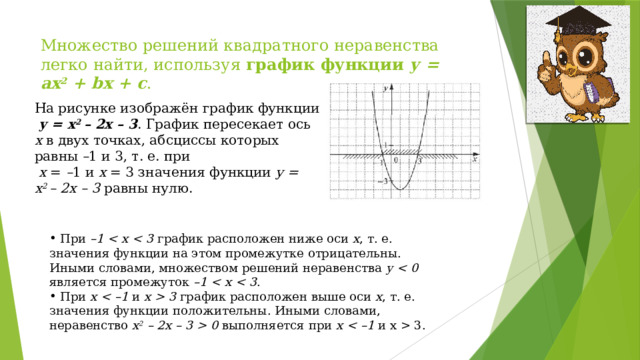
Множество решений квадратного неравенства легко найти, используя график функции у = ах 2 + bх + с .
На рисунке изображён график функции у = х 2 – 2х – 3 . График пересекает ось х в двух точках, абсциссы которых равны – 1 и 3, т. е. при х = – 1 и х = 3 значения функции у = х 2 – 2х – 3 равны нулю.
- При –1 график расположен ниже оси х , т. е. значения функции на этом промежутке отрицательны. Иными словами, множеством решений неравенства у является промежуток –1 .
- При x и x 3 график расположен выше оси х , т. е. значения функции положительны. Иными словами, неравенство х 2 – 2х – 3 0 выполняется при х и х 3.

При решении квадратных неравенств можно ограничиться схематическим рисунком, показывающим положение графика относительно оси х , так как координаты вершины в данном вопросе значения не имеют; можно также не изображать ось у .
Если требуется решить квадратное неравенство с отрицательным коэффициентом а , то всегда целесообразно перейти к равносильному неравенству с положительным первым коэффициентом, умножив обе части неравенства на – 1. Например, вместо неравенства 5 + 4х – х 2 ≤ 0 решать неравенство х 2 – 4х – 5 ≥ 0.
 0 . Выясним, пересекает ли график функции у = х 2 – х – 6 ось х. Для этого решим уравнение х 2 – x – 6 = 0. Его корни x 1 = – 2 и х 2 = 3. Следовательно, парабола (график функции) пересекает ось х в точках с абсциссами – 2 и 3, её ветви направлены вверх. Покажем схематически расположение параболы относительно оси х. Из рисунка видно, что парабола расположена выше оси x при х – 2 и х 3. Объединение этих промежутков и составляет множество решений неравенства x 2 – x – 6 0. Ответ можно записать двумя способами: 1) x – 2; х 3; 2) ( – ∞ ; – 2) U (3; + ∞ ). " width="640"
0 . Выясним, пересекает ли график функции у = х 2 – х – 6 ось х. Для этого решим уравнение х 2 – x – 6 = 0. Его корни x 1 = – 2 и х 2 = 3. Следовательно, парабола (график функции) пересекает ось х в точках с абсциссами – 2 и 3, её ветви направлены вверх. Покажем схематически расположение параболы относительно оси х. Из рисунка видно, что парабола расположена выше оси x при х – 2 и х 3. Объединение этих промежутков и составляет множество решений неравенства x 2 – x – 6 0. Ответ можно записать двумя способами: 1) x – 2; х 3; 2) ( – ∞ ; – 2) U (3; + ∞ ). " width="640"
Пример 1
Решим неравенство х 2 – x – 6 0 .
Выясним, пересекает ли график функции у = х 2 – х – 6 ось х. Для этого решим уравнение х 2 – x – 6 = 0. Его корни x 1 = – 2 и х 2 = 3. Следовательно, парабола (график функции) пересекает ось х в точках с абсциссами – 2 и 3, её ветви направлены вверх. Покажем схематически расположение параболы относительно оси х.
Из рисунка видно, что парабола расположена выше оси x при х – 2 и х 3. Объединение этих промежутков и составляет множество решений неравенства x 2 – x – 6 0.
Ответ можно записать двумя способами: 1) x – 2; х 3; 2) ( – ∞ ; – 2) U (3; + ∞ ).
 2 . Раскроем скобки и перенесём все слагаемые в левую часть, получим: – 2x 2 + 3x – 2 0. Теперь заменим неравенство равносильным неравенством с положительным первым коэффициентом (для этого умножим обе части неравенства на – 1 и заменим знак неравенства на противоположный): 2х 2 – 3х + 2 Выясним, пересекает ли парабола – график функции у = 2х 2 – 3х + 2 – ось х . Найдём дискриминант квадратного трёхчлена 2х 2 – 3х + 2, a именно: D = 9 – 4·2·2 = 9 – 16 При всех значениях х парабола расположена выше оси х , это означает, что нет таких значений х, при которых функция у = 2х 2 – 3х + 2 принимает отрицательные значения, значит, неравенство 2х 2 – Зх + 2 Ответ можно записать двумя способами: 1) неравенство решений не имеет; 2) ∅. " width="640"
2 . Раскроем скобки и перенесём все слагаемые в левую часть, получим: – 2x 2 + 3x – 2 0. Теперь заменим неравенство равносильным неравенством с положительным первым коэффициентом (для этого умножим обе части неравенства на – 1 и заменим знак неравенства на противоположный): 2х 2 – 3х + 2 Выясним, пересекает ли парабола – график функции у = 2х 2 – 3х + 2 – ось х . Найдём дискриминант квадратного трёхчлена 2х 2 – 3х + 2, a именно: D = 9 – 4·2·2 = 9 – 16 При всех значениях х парабола расположена выше оси х , это означает, что нет таких значений х, при которых функция у = 2х 2 – 3х + 2 принимает отрицательные значения, значит, неравенство 2х 2 – Зх + 2 Ответ можно записать двумя способами: 1) неравенство решений не имеет; 2) ∅. " width="640"
Пример 2
Решим неравенство х(3 – 2х) 2 .
Раскроем скобки и перенесём все слагаемые в левую часть, получим: – 2x 2 + 3x – 2 0. Теперь заменим неравенство равносильным неравенством с положительным первым коэффициентом (для этого умножим обе части неравенства на – 1 и заменим знак неравенства на противоположный): 2х 2 – 3х + 2
Выясним, пересекает ли парабола – график функции у = 2х 2 – 3х + 2 – ось х . Найдём дискриминант квадратного трёхчлена 2х 2 – 3х + 2, a именно: D = 9 – 4·2·2 = 9 – 16
При всех значениях х парабола расположена выше оси х , это означает, что нет таких значений х, при которых функция у = 2х 2 – 3х + 2 принимает отрицательные значения, значит, неравенство 2х 2 – Зх + 2
Ответ можно записать двумя способами: 1) неравенство решений не имеет; 2) ∅.

Пример 3 Найдём область определения:
Область определения выражения задаётся условиями:
Решив каждое из неравенств, получим:
Сделаем схематический рисунок:
Из рисунка видно, что множеством решений системы неравенств является промежуток от 2/3 до 2 (включая эти числа) без числа 1. Ответ можно записать несколькими способами:

Рассмотри решение №305 (пример а )

Рассмотри решение №305 (пример в )

Рассмотри решение №320 (пример а )

Рефлексия
Мне все понятно.
Ничего не понятно.
У меня все получилось
Требуется помощь.
Есть затруднения.
Но я обязательно разберусь.

Домашнее задание
- Прочитать пункт 16.
- Решить №305 (б), №306 (а, б, е) №320 (б)

Использованные источники
- https://uchitel.pro/ квадратные-неравенства /
- https:// pdf.11klasov.net/1384-algebra-9-klass-uchebnik-makarychev-yun-mindyuk-ng-i-dr.html
- https:// interneturok.ru/lesson/algebra/9-klass/itogovoe-povtorenie-kursa-algebry-9go-klassa/kvadratnye-neravenstva









 0, где а ≠ 0, называют квадратным неравенством. Примечание к определению: вместо знака могут стоять и другие знаки неравенства: " width="640"
0, где а ≠ 0, называют квадратным неравенством. Примечание к определению: вместо знака могут стоять и другие знаки неравенства: " width="640"
 3 график расположен выше оси х , т. е. значения функции положительны. Иными словами, неравенство х 2 – 2х – 3 0 выполняется при х и х 3. " width="640"
3 график расположен выше оси х , т. е. значения функции положительны. Иными словами, неравенство х 2 – 2х – 3 0 выполняется при х и х 3. " width="640"

 0 . Выясним, пересекает ли график функции у = х 2 – х – 6 ось х. Для этого решим уравнение х 2 – x – 6 = 0. Его корни x 1 = – 2 и х 2 = 3. Следовательно, парабола (график функции) пересекает ось х в точках с абсциссами – 2 и 3, её ветви направлены вверх. Покажем схематически расположение параболы относительно оси х. Из рисунка видно, что парабола расположена выше оси x при х – 2 и х 3. Объединение этих промежутков и составляет множество решений неравенства x 2 – x – 6 0. Ответ можно записать двумя способами: 1) x – 2; х 3; 2) ( – ∞ ; – 2) U (3; + ∞ ). " width="640"
0 . Выясним, пересекает ли график функции у = х 2 – х – 6 ось х. Для этого решим уравнение х 2 – x – 6 = 0. Его корни x 1 = – 2 и х 2 = 3. Следовательно, парабола (график функции) пересекает ось х в точках с абсциссами – 2 и 3, её ветви направлены вверх. Покажем схематически расположение параболы относительно оси х. Из рисунка видно, что парабола расположена выше оси x при х – 2 и х 3. Объединение этих промежутков и составляет множество решений неравенства x 2 – x – 6 0. Ответ можно записать двумя способами: 1) x – 2; х 3; 2) ( – ∞ ; – 2) U (3; + ∞ ). " width="640"
 2 . Раскроем скобки и перенесём все слагаемые в левую часть, получим: – 2x 2 + 3x – 2 0. Теперь заменим неравенство равносильным неравенством с положительным первым коэффициентом (для этого умножим обе части неравенства на – 1 и заменим знак неравенства на противоположный): 2х 2 – 3х + 2 Выясним, пересекает ли парабола – график функции у = 2х 2 – 3х + 2 – ось х . Найдём дискриминант квадратного трёхчлена 2х 2 – 3х + 2, a именно: D = 9 – 4·2·2 = 9 – 16 При всех значениях х парабола расположена выше оси х , это означает, что нет таких значений х, при которых функция у = 2х 2 – 3х + 2 принимает отрицательные значения, значит, неравенство 2х 2 – Зх + 2 Ответ можно записать двумя способами: 1) неравенство решений не имеет; 2) ∅. " width="640"
2 . Раскроем скобки и перенесём все слагаемые в левую часть, получим: – 2x 2 + 3x – 2 0. Теперь заменим неравенство равносильным неравенством с положительным первым коэффициентом (для этого умножим обе части неравенства на – 1 и заменим знак неравенства на противоположный): 2х 2 – 3х + 2 Выясним, пересекает ли парабола – график функции у = 2х 2 – 3х + 2 – ось х . Найдём дискриминант квадратного трёхчлена 2х 2 – 3х + 2, a именно: D = 9 – 4·2·2 = 9 – 16 При всех значениях х парабола расположена выше оси х , это означает, что нет таких значений х, при которых функция у = 2х 2 – 3х + 2 принимает отрицательные значения, значит, неравенство 2х 2 – Зх + 2 Ответ можно записать двумя способами: 1) неравенство решений не имеет; 2) ∅. " width="640"
























