Презентация к уроку геометрии на тему "Сумма углов треугольника".

« Вдохновение нужно в геометрии

не меньше, чем в поэзии »

А.С. Пушкин

ЦЕЛИ УРОКА:

• Формировать умение доказывать теорему о сумме углов

треугольника, решать простейшие задачи по данной теме.

• Развивать универсальные логические действия:

сравнение, анализ, выдвижение гипотез, их обоснование,

установление причинно-следственных связей, построение

логических цепочек рассуждений, проведение

доказательств; умение ставить цель и планировать её;

умение осуществлять культурную коммуникацию

с учителем и со сверстниками, работая в паре.

• Развивать навыки контроля и самоконтроля, прививать

навыки по сохранению и укреплению своего здоровья.

• Воспитывать целеустремленность, способность

преодолевать трудности при решении учебной задачи.

.

План урока.

• Организационный момент. Актуализация знаний учащихся. Открытие новых знаний. Изучение нового материала. Первичное закрепление изученного. Усвоение знаний. Решение задач. Физминутка. Самостоятельная работа. Домашнее задание. Рефлексия. Итог урока.
• Организационный момент.
• Актуализация знаний учащихся.
• Открытие новых знаний. Изучение нового материала.
• Первичное закрепление изученного.
• Усвоение знаний. Решение задач.
• Физминутка.
• Самостоятельная работа.
• Домашнее задание.
• Рефлексия. Итог урока.

Бермудский треугольник. Атлантический океан.

Скульптура невозможного треугольника.

Бельгия.

Треугольник Пенроуза. Австралия.

Фалес,

(640/624 — 548/545 до н. э.)

,

Из истории геометрии

Треугольник всегда имел широкое применение в практической жизни. Так, в строительном искусстве испокон веков используется свойство жесткости треугольника для укрепления различных строений и их деталей. Изображение треугольников и задачи на треугольники встречаются в папирусах, в старинных индийских книгах и других древних документах.

В древней Греции учение о треугольнике развивалось в ионийской школе, основанной в VII веке до нашей эры Фалесом, в школе Пифагора и других; оно было затем полностью изложено в первой книге "Начал" Евклида.

,

Из истории геометрии

Среди "определений", которыми начинается эта книга, имеются и следующие: "Из трехсторонних фигур равносторонний треугольник есть фигура, имеющая три равные стороны, равнобедренный же – имеющая только две равные стороны, разносторонний – имеющая три неравные стороны".

Понятие о треугольнике исторически развивалось, по-видимому, так: сначала рассматривались лишь правильные, затем равнобедренные и, наконец, разносторонние треугольники.

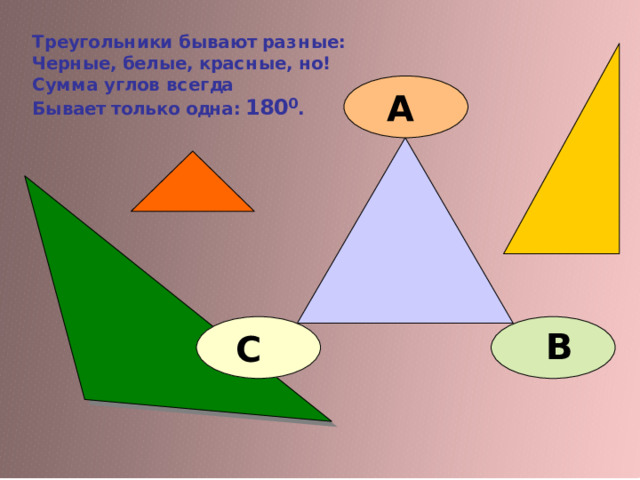
СУММА УГЛОВ ТРЕУГОЛЬНИКА

В

?

?

?

А

С

 A +  B +  C =

?

Исследование №1

1

1

2

3

2

3

3

2

1

Исследование №2

2

1

3

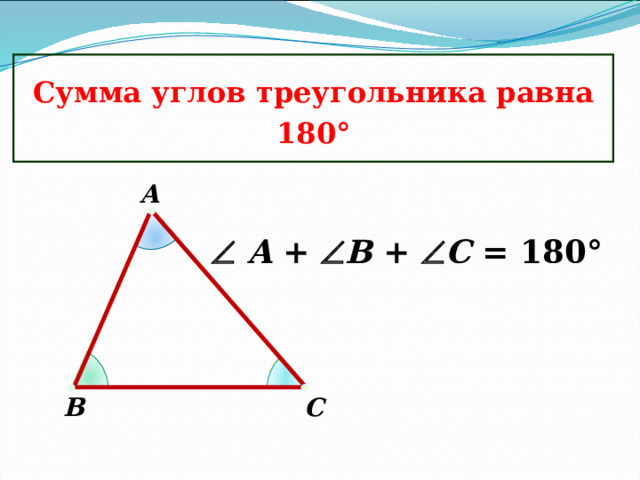
Сумма углов треугольника равна 180 °

А

 A +  B +  C = 180°

C

В

13

• Легче остановить Солнце, легче двинуть Землю, чем уменьшить сумму углов треугольника...

В.Ф. Каган

(1869 - 1953)

Теорема: Сумма углов треугольника равна 180 0

К

Дано: треугольник АВС

Доказать: АВС+ ВСА+ ВАС= 180 0

Доказательство

КТ // ВС, А € КТ, КАТ= КАВ+ ВАС+ САТ

1, 4- внутренние накрест лежащие при прямых КТ // ВС, и секущей АВ

Значит 1= 4

3, 5- внутренние накрест лежащие при прямых КТ // ВС, и секущей АС

Значит 3= 5 .

КАТ – развернутый угол. КАТ= 180 0

Очевидно, 4+ 2+ 5=180 0

Отсюда, 1+ 2+ 3=180 0 ч.т.д.

Т

А

5

4

2

1

3

В

C

Назад, в историю!

Свойство суммы углов треугольника было установлено еще в Древнем Египте.

Доказательво, изложенное в современных учебниках, содержится в комментариях Прокла к «Началам» Евклида.

Прокл утверждает, что это доказательство было открыто пифагорийцами (5 в. до н. э.).

Прокл пишет: «Пифагор впервые разработал принципы геометрии».

В первой книге «Начал» Евклид излагает другое доказательство теоремы о сумме углов треугольника, которое легко понять при помощи чертежа.

К

Так доказывают теорему о сумме углов треугольника в школах Японии

1

3

2

5

4

Звездочёт

Электронная физминутка

Решение задач по готовым чертежам

«Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их».

Д. Пойа

?

?

Самостоятельная работа

"Нельзя изучать

математику,

глядя, как это

делает сосед"

А.Нивен

1.

2.

3.

4.

5.

40°

80°

30°

?

20°

40°

?

?

?

?

35°

6. (дополнительный номер) Углы треугольника относятся как 2:3:4. Найдите углы этого треугольника.

17

01/07/2022

Взаимопроверка

« 5 » - (всё решено правильно)

« 4 » - (допущена одна ошибка)

« 3 » - (допущено две – три ошибки)

1. 180 0 – (40 0 + 80 0 ) = 180 0 – 120 0 = 60 0 2. 180 0 – (30 0 + 20 0 ) = 180 0 – 50 0 = 130 0 3. 180 0 – (35 0 + 35 0 ) = 180 0 – 70 0 = 110 0 4. (180 0 – 90 0 ) : 2 = 90 0 : 2 = 45 0 5. (180 0 – 40 0 ) : 2 = 140 0 : 2 = 70 0

Решите задачу:

Дано: ΔАВС,  А:  В:  С = 2:3:4

Найти:  А,  В,  С

Решение.

Пусть одна часть углов составляет х  , тогда  А = 2х  ,  В = 3х  ,  С = 4х  . Т. к. по теореме о сумме углов треугольника  А+  В+  С=180  , то получим уравнение 2х+3х+4х =180, 9х =180, х =20.

20  - одна часть углов.

 А = 2  20  = 40  ,  В = 3  20  = 60  ,  С = 4  20  = 80  .

Ответ: 40  , 60  , 80  .

В

А

С

Закончите приведенные ниже предложения, чтобы получились верные утверждения:

• Сумма углов произвольного треугольника равна…?
• Если один из углов треугольника тупой, то остальные…?
• Если один из углов треугольника прямой, то остальные…?
• Если один из углов равнобедренного треугольника равен 60°, то треугольник…?

Участвовал в открытии нового

Выполнял правила работы в паре, группе.

Все получилось!

Справился с затруднением

Надо тренироваться

Оцени себя!

«Нет ничего дороже для человека того, чтобы хорошо мыслить.»

Л. Н. Толстой

Домашнее задание.

Доказательство теоремы одним из способов

1) п. 33, № 18, №21 стр. 53;

2) п. 33, №22, №26 стр. 53;

3) п. 33, №25, № 28 стр.53

+ доказать теорему о сумме углов

треугольника различными способами.