Презентация к уроку "Параллельные прямые"

Геометрия 7Б класс.

По каким рельсам не поедет поезд?

Почему?

Параллельные прямые.

Определение.

а

b

Две прямые на плоскости называются

ПАРАЛЛЕЛЬНЫМИ , если они не пересекаются.

Перечислите

• 1. Где вы встречают параллельные прямые?
• 2. Люди каких профессий каждый день видят перед собой параллельные прямые?
• 3. Можно ли всегда распознать параллельные прямые?
• 4. С помощью каких инструментов можно проверить параллельность прямых?

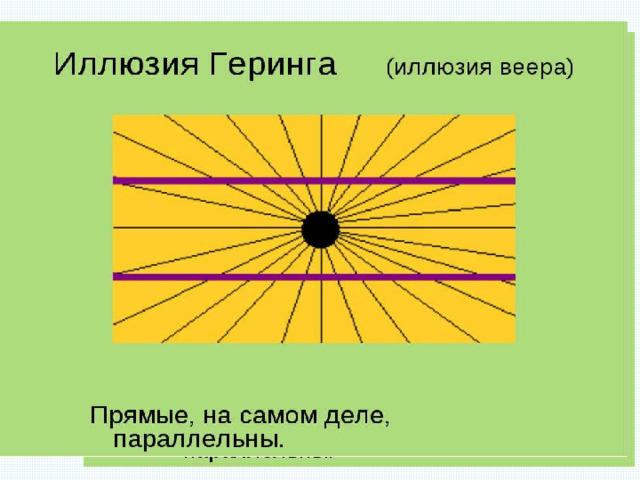
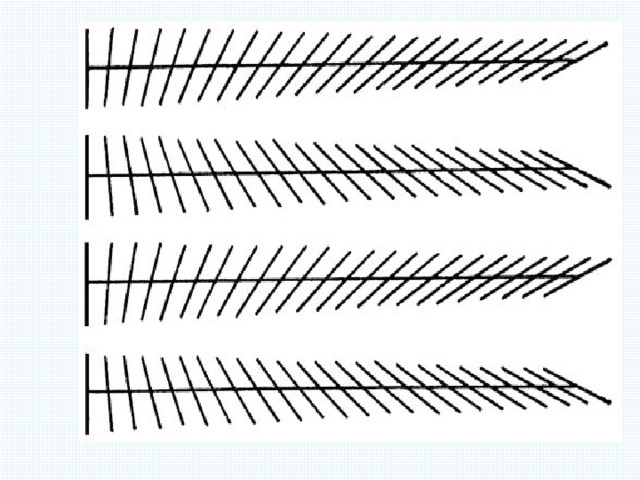
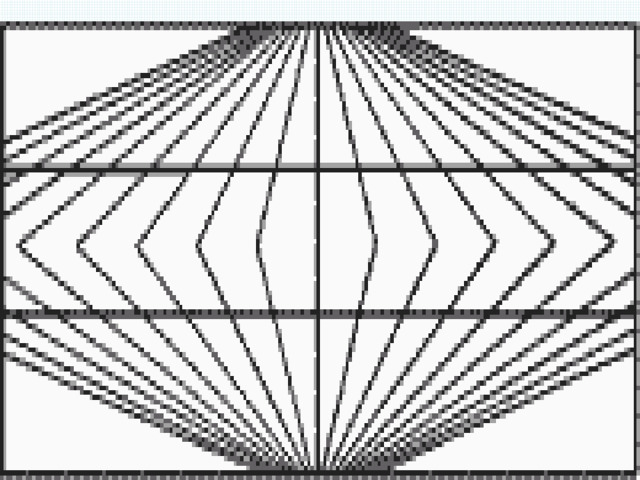
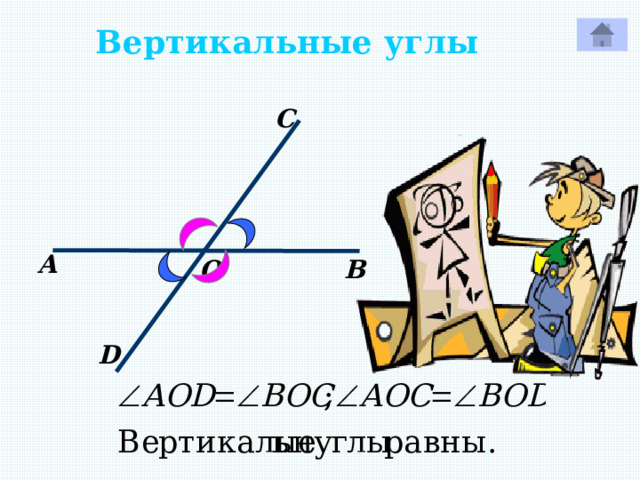
Вертикальные углы

C

А

В

О

D

Смежные углы

В

А

О

C

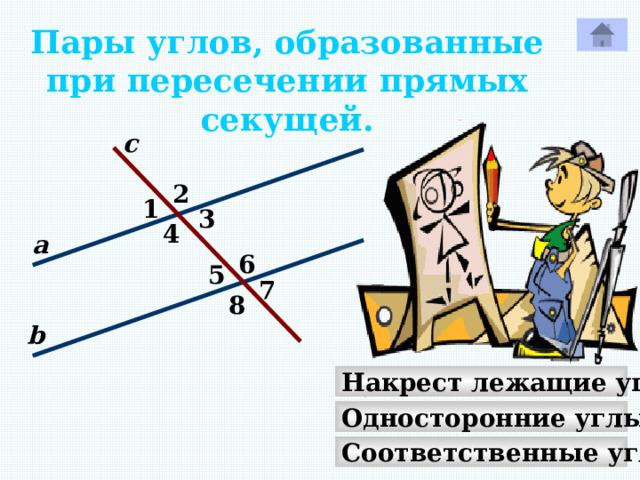
Пары углов, образованные

при пересечении прямых

секущей.

с

2

1

3

4

а

6

5

7

Р

8

b

Накрест лежащие углы

Односторонние углы

Соответственные углы

Каким общим словом можно назвать приметы прихода весны

Признаки весны

• Тает снег
• Бегут ручьи
• Появляются проталины
• Расцветают подснежники
• На деревьях распускаются почки

Признак параллельности

двух прямых

по накрест лежащим углам.

a ıı b

с

2

1

а

3

4

Р

b

Если при пересечении двух прямых секущей

НАКРЕСТ ЛЕЖАЩИЕ углы равны,

то прямые параллельны

Признак параллельности

двух прямых

по соответственным углам.

a ıı b

с

2

1

3

4

а

6

5

7

Р

8

b

Если при пересечении двух прямых секущей

СООТВЕТСТВЕННЫЕ углы равны.

то прямые параллельны

Признак параллельности

двух прямых

по односторонним углам.

a ıı b

с

2

1

а

3

4

Р

b

Если при пересечении двух прямых секущей

сумма ОДНОСТОРОННИХ углов равна 180 0 ,

то прямые параллельны

Аксиома параллельных прямых.

а

А

b

Через точку, не лежащую на данной прямой,

проходит только одна прямая,

параллельная данной.

Следствие из аксиомы

параллельных прямых.

1 0

a ıı b

с

а

b

Если прямая пересекает одну из двух

параллельных прямых, то она

пересекает и другую.

Следствие из аксиомы

параллельных прямых.

2 0

а

с

b

a ıı b

Если две прямые параллельны третьей прямой,

то они параллельны.

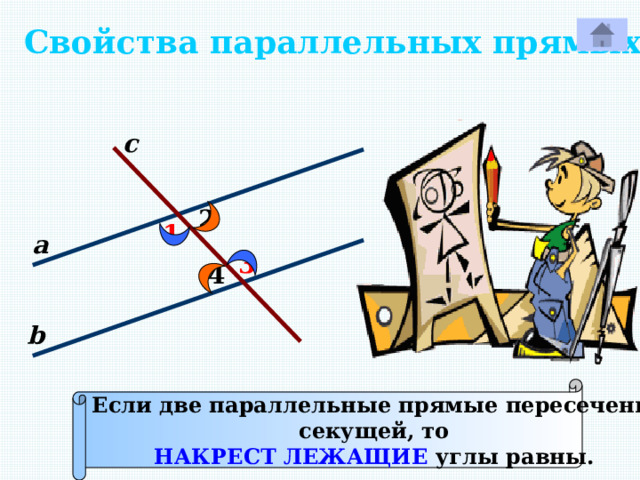
Свойства параллельных прямых.

с

2

1

а

3

4

Р

b

Если две параллельные прямые пересечены

секущей, то

НАКРЕСТ ЛЕЖАЩИЕ углы равны.

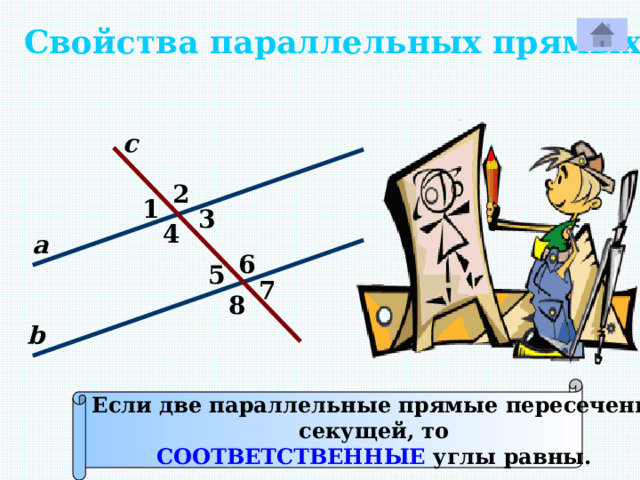
Свойства параллельных прямых.

с

2

1

3

4

а

6

5

7

Р

8

b

Если две параллельные прямые пересечены

секущей, то

СООТВЕТСТВЕННЫЕ углы равны.

Свойства параллельных прямых.

с

2

1

а

3

4

Р

b

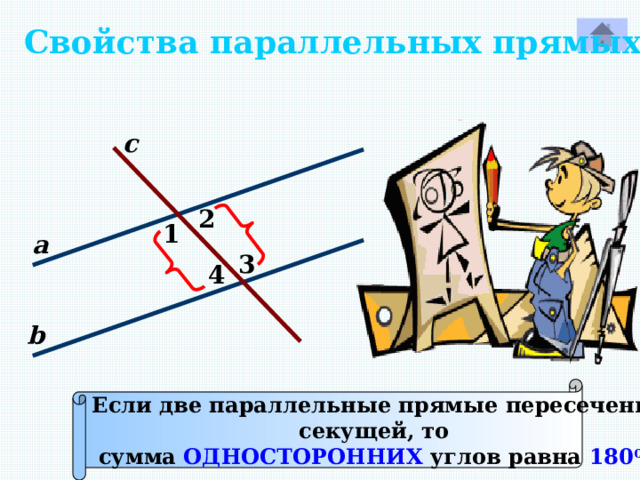
Если две параллельные прямые пересечены

секущей, то

сумма ОДНОСТОРОННИХ углов равна 180 0 .

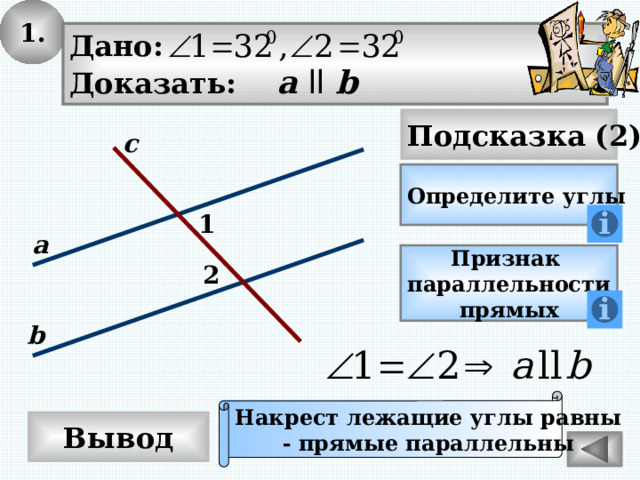
1.

Дано:

Доказать: а ll b

Подсказка (2)

с

Определите углы

1

а

Признак

параллельности

прямых

2

b

Накрест лежащие углы равны

- прямые параллельны

Вывод

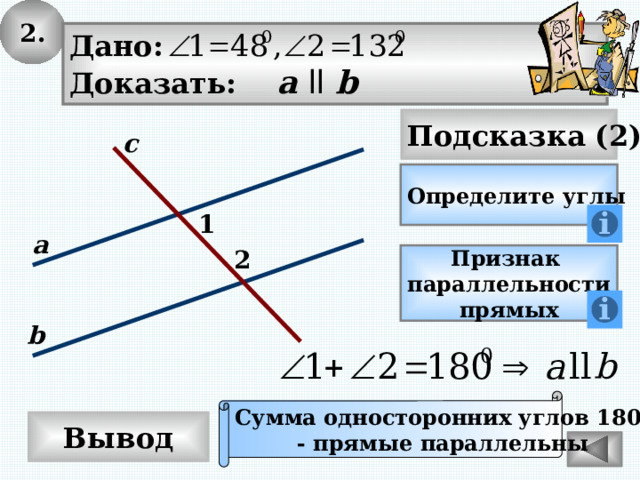
2.

Дано:

Доказать: а ll b

Подсказка (2)

с

Определите углы

1

а

2

Признак

параллельности

прямых

b

Сумма односторонних углов 180 0

- прямые параллельны

Вывод

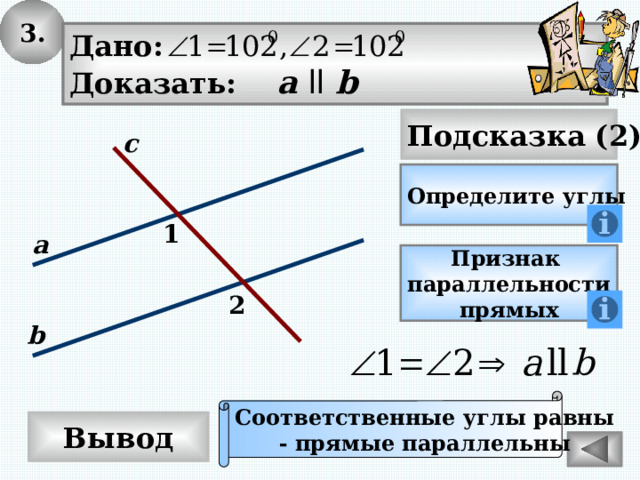
3.

Дано:

Доказать: а ll b

Подсказка (2)

с

Определите углы

1

а

Признак

параллельности

прямых

2

b

Соответственные углы равны

- прямые параллельны

Вывод

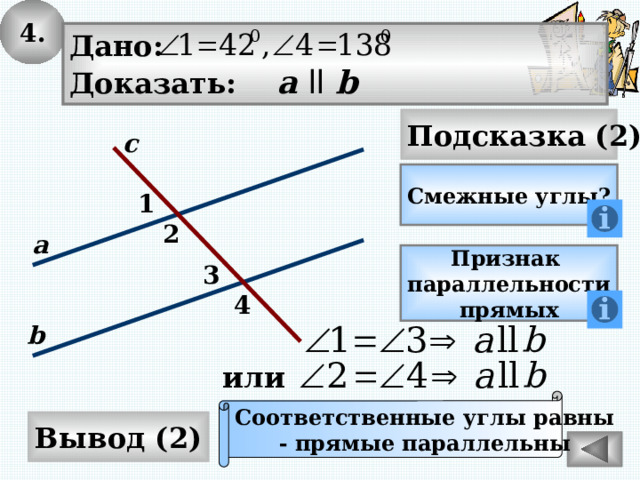
4.

Дано:

Доказать: а ll b

Подсказка (2)

с

Смежные углы?

1

2

а

Признак

параллельности

прямых

3

4

b

или

Соответственные углы равны

- прямые параллельны

Вывод (2)

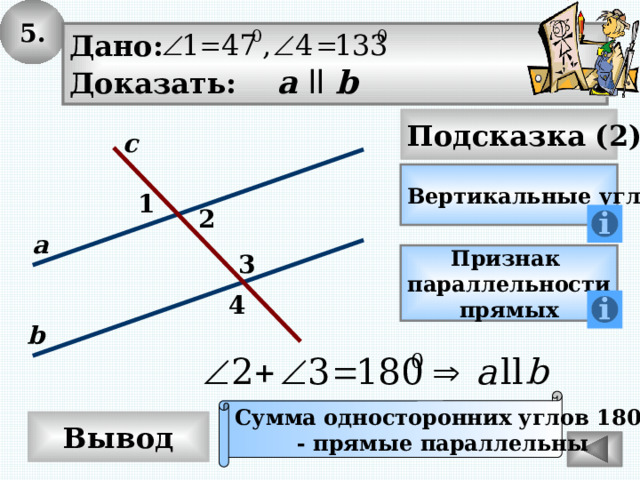
5.

Дано:

Доказать: а ll b

Подсказка (2)

с

Вертикальные углы?

1

2

а

3

Признак

параллельности

прямых

4

b

Сумма односторонних углов 180 0

- прямые параллельны

Вывод

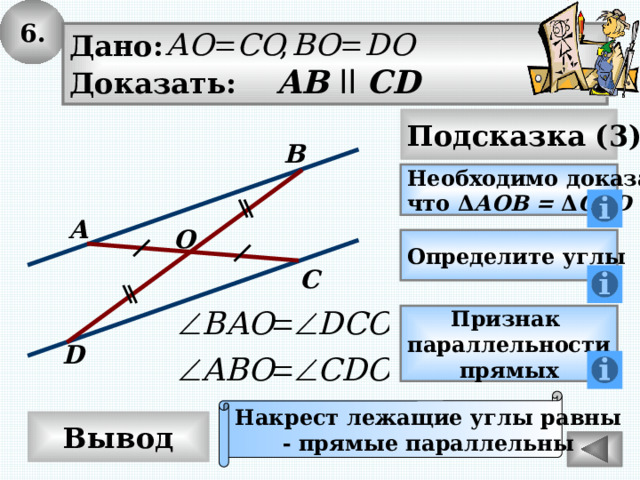
6.

Дано:

Доказать: AB ll CD

Подсказка (3)

B

Необходимо доказать,

что Δ АОВ = Δ COD

A

O

Определите углы

C

Признак

параллельности

прямых

D

Накрест лежащие углы равны

- прямые параллельны

Вывод

7.

Дано:

Доказать: a ll c

Подсказка (3)

1

a

Углы 1 и 2…

Признак?

2

b

4

Определите углы

3 и 2

c

3

d

Следствие из аксиомы

параллельных

прямых

Если две прямые параллельны

третьей прямой, то они

параллельны

Вывод

8.

Дано:

Доказать: a ll c

Подсказка (3)

1

a

4

Вертикальные

углы

2

b

Определите углы

3 и 2

3

c

d

Следствие из аксиомы

параллельных

прямых

Если две прямые параллельны

третьей прямой, то они

параллельны

Вывод

9.

Дано:

Какие из прямых параллельны?

Подсказка (3)

1

a

Вертикальные

углы

b

2

Смежные углы

c

3

Виды углов

d

Вывод

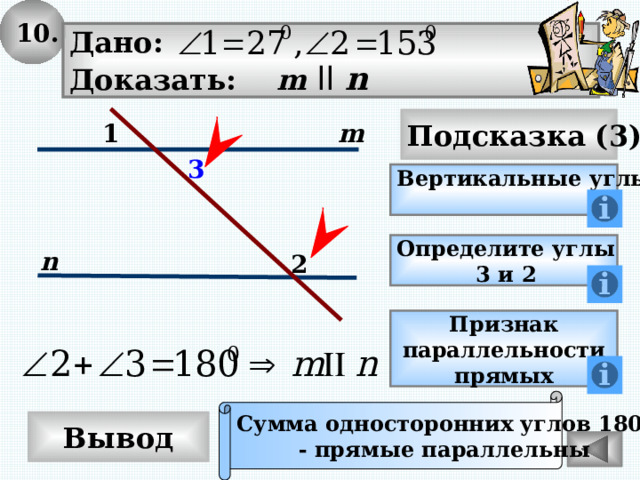
10.

Дано:

Доказать: m ll n

Подсказка (3)

1

m

3

Вертикальные углы

Определите углы

3 и 2

n

2

Признак

параллельности

прямых

Сумма односторонних углов 180 0

- прямые параллельны

Вывод

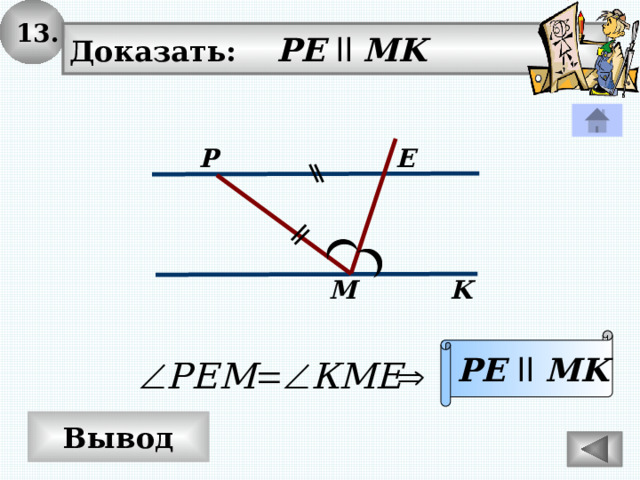
13.

Доказать: PE ll MK

P

E

M

K

PE ll MK

Вывод

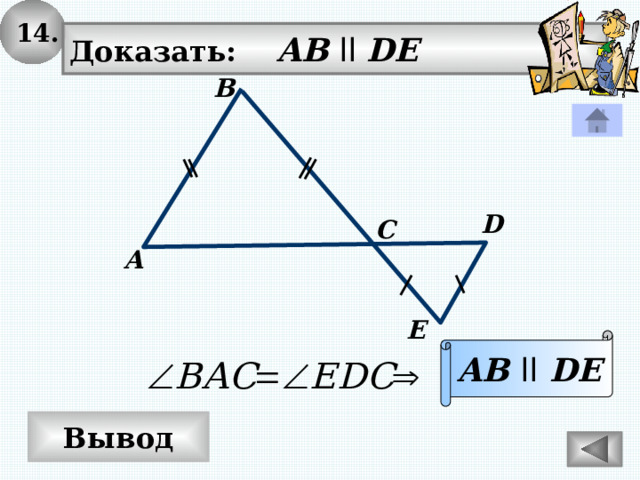
14.

Доказать: AB ll DE

B

D

C

A

E

AB ll DE

Вывод

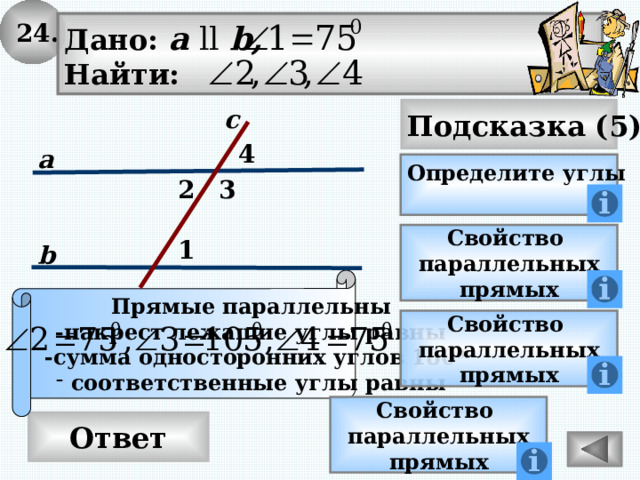
24.

Дано: а ll b,

Найти:

Подсказка (5)

с

4

а

Определите углы

2

3

Свойство

параллельных

прямых

1

b

Прямые параллельны

-накрест лежащие углы равны

-сумма односторонних углов 180 0

• соответственные углы равны

Свойство

параллельных

прямых

Свойство

параллельных

прямых

Ответ

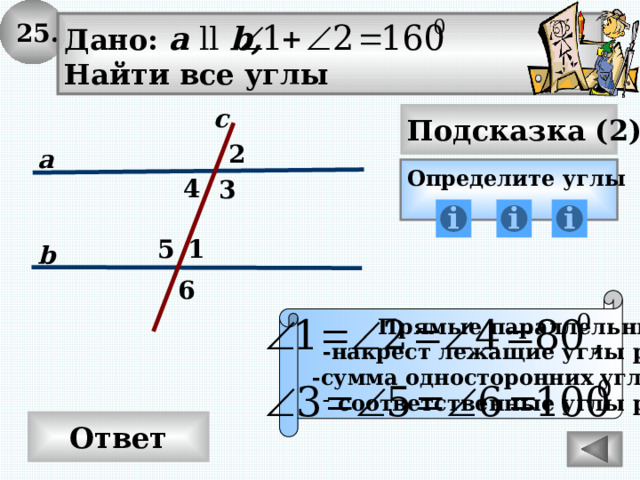
25.

Дано: а ll b,

Найти все углы

с

Подсказка (2)

2

а

Определите углы

4

3

1

5

b

6

Прямые параллельны

-накрест лежащие углы равны

-сумма односторонних углов 180 0

• соответственные углы равны

Ответ

15.

Выберите верные утверждения:

- вертикальные

- односторонние

с

а

6

- соответственные

1

3

8

- накрест лежащие

- смежные

b

5

7

4

2

- накрест лежащие

- односторонние

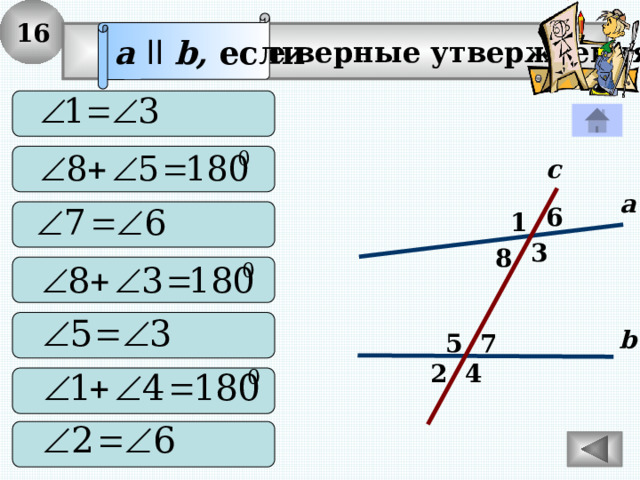
16

a ll b, если

Выберите верные утверждения:

с

а

6

1

3

8

b

7

5

4

2

21.

НЕ СООТВЕТСТВУЕТ

Прямые не параллельны, если при

пересечении двух прямых секущей:

сумма односторонних углов не равна 180 0 .

сумма соответственных углов равна 180 0 .

вертикальные углы равны .

накрест лежащие углы не равны .

сумма смежных углов не равна 180 0 .

соответственные углы не равны .

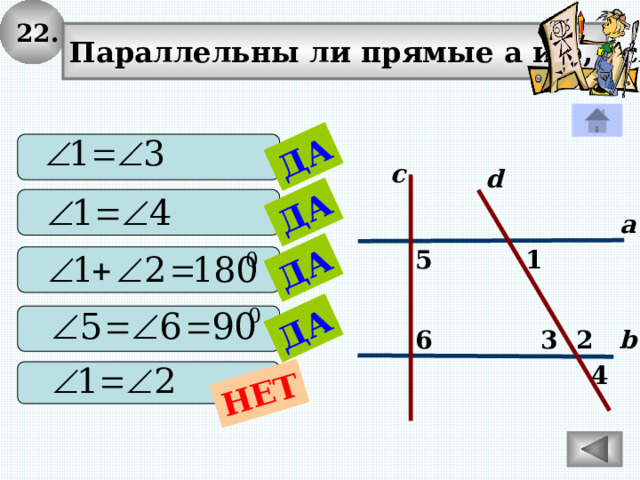
22.

ДА

ДА

ДА

ДА

НЕТ

Параллельны ли прямые а и b, если

с

d

а

5

1

b

6

3

2

4

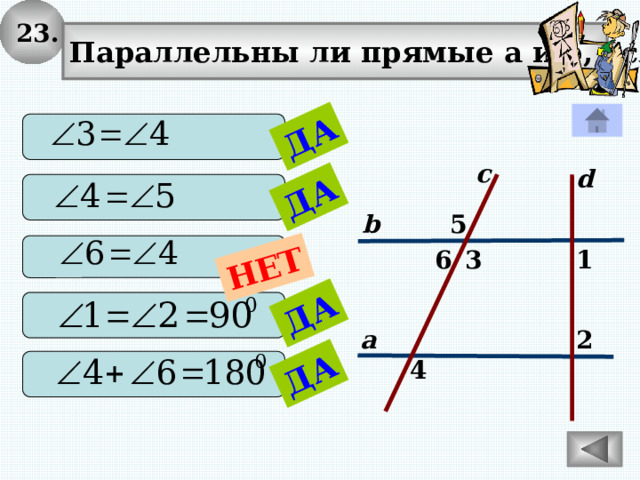
23.

ДА

ДА

ДА

ДА

НЕТ

Параллельны ли прямые а и b, если

с

d

5

b

6

3

1

а

2

4

Первый признак

равенства треугольников.

А 1

А

В

В 1

С

С 1

По двум сторонам и углу между ними.

Второй признак

равенства треугольников.

А 1

А

С

С 1

В 1

В

По стороне и прилежащим к ней углам.

Третий признак

равенства треугольников.

А

А 1

С 1

С

В 1

В

По трём сторонам.

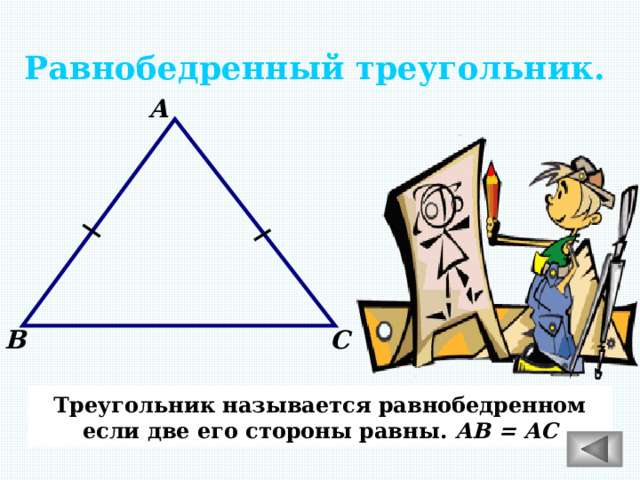
Равнобедренный треугольник.

А

В

С

Треугольник называется равнобедренном

если две его стороны равны. АВ = АС

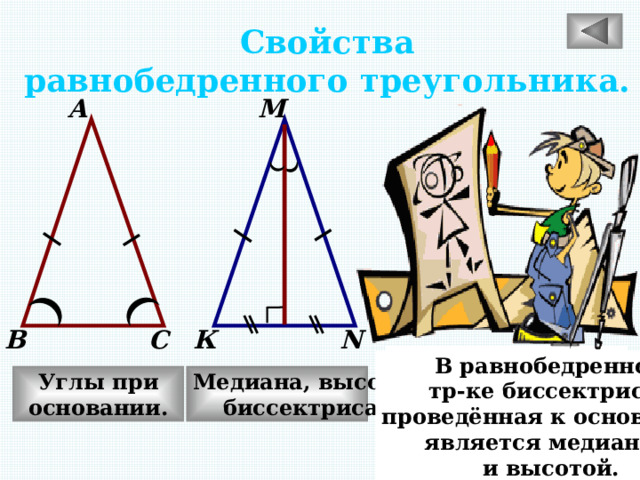
Свойства

равнобедренного треугольника.

М

А

В

N

К

С

В равнобедренном

треугольнике углы

при основании равны.

В равнобедренном

тр-ке биссектриса,

проведённая к основанию,

является медианой

и высотой.

Медиана, высота,

Углы при

основании.

биссектриса.