Просмотр содержимого документа
«Презентация к уроку "Первообразная и интеграл"»

Первообразная и интеграл

Первообразная
- Функция F(x) называется первообразной для функции f(x) на данном промежутке, если для любого x из этого промежутка
Пример:
Первообразной для функции на всей
числовой оси является , поскольку
Действие нахождения первообразной функции называется интегрированием.
Основное свойство первообразных
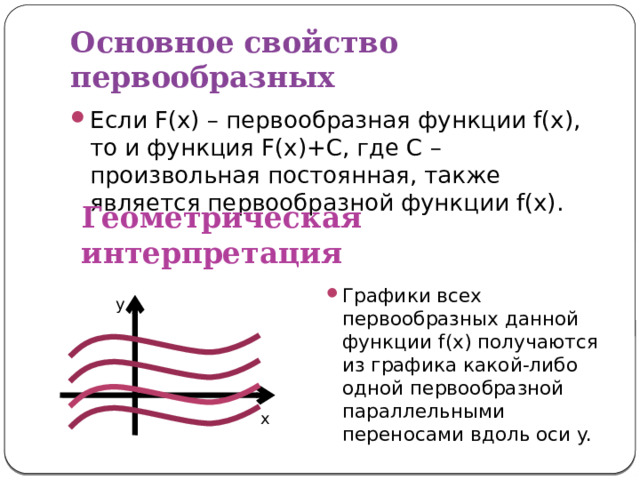
- Если F(x) – первообразная функции f(x), то и функция F(x)+C, где C – произвольная постоянная, также является первообразной функции f(x).
Геометрическая интерпретация
- Графики всех первообразных данной функции f(x) получаются из графика какой-либо одной первообразной параллельными переносами вдоль оси y.
y
x
![№ 7(ЕГЭ профильный уровень). На рисунке изображён график функции y = F(x) — одной из первообразных функции f(x), определённой на интервале (−3; 5). Найдите количество решений уравнения f(x)=0 на отрезке [−2; 4]. 10](https://fsd.multiurok.ru/html/2021/03/20/s_6055c3baa9e9e/img3.jpg)
№ 7(ЕГЭ профильный уровень). На рисунке изображён график функции y = F(x) — одной из первообразных функции f(x), определённой на интервале (−3; 5). Найдите количество решений уравнения f(x)=0 на отрезке [−2; 4].
10

Неопределенный интеграл
- Совокупность всех первообразных данной функции f(x) называется ее неопределенным интегралом и обозначается :
,
где C – произвольная постоянная .

Правила интегрирования

Таблица первообразных
![Определенный интеграл В прямоугольной системе координат XOY фигура, ограниченная осью OX, прямыми , и графиком непрерывной неотрицательной на отрезке [ a;b ] функции , называется криволинейной трапецией](https://fsd.multiurok.ru/html/2021/03/20/s_6055c3baa9e9e/img7.jpg)
Определенный интеграл
В прямоугольной системе координат XOY фигура, ограниченная осью OX, прямыми ,
и графиком непрерывной неотрицательной на отрезке [ a;b ] функции , называется криволинейной трапецией
![Определенный интеграл Вычислим площадь криволинейной трапеции. который называют определенным интегралом от функции по отрезку [a;b] и обозначают так:](https://fsd.multiurok.ru/html/2021/03/20/s_6055c3baa9e9e/img8.jpg)
Определенный интеграл
Вычислим площадь криволинейной трапеции.
который называют
определенным интегралом
от функции
по отрезку [a;b] и обозначают так:

Связь между определенным интегралом и первообразной (Формула Ньютона - Лейбница)
где F(x) – первообразная функции f(x).
![Геометрический смысл определенного интеграла Площадь криволинейной трапеции, ограниченной графиком непрерывной положительной на промежутке [ a;b ] функции f(x) , осью x и прямыми x=a и x= b :](https://fsd.multiurok.ru/html/2021/03/20/s_6055c3baa9e9e/img10.jpg)
Геометрический смысл определенного интеграла
Площадь криволинейной трапеции, ограниченной графиком непрерывной положительной на промежутке [ a;b ] функции f(x) , осью x и прямыми x=a и x= b :

Площадь криволинейной трапеции
где F(x) – первообразная функции f(x).
![Площадь фигуры, Ограниченной графиками непрерывных функций y=f(x) и y=g(x) таких, что для любого x из [a;b], где a и b – абсциссы точек пересечения графиков функций:](https://fsd.multiurok.ru/html/2021/03/20/s_6055c3baa9e9e/img12.jpg)
Площадь фигуры,
- Ограниченной графиками непрерывных функций y=f(x) и y=g(x) таких, что
для любого x из [a;b], где a и b – абсциссы точек пересечения графиков функций:

№ 7(ЕГЭ профильный уровень). На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите F(8) − F(2), где F(x) — одна из первообразных функции f(x).
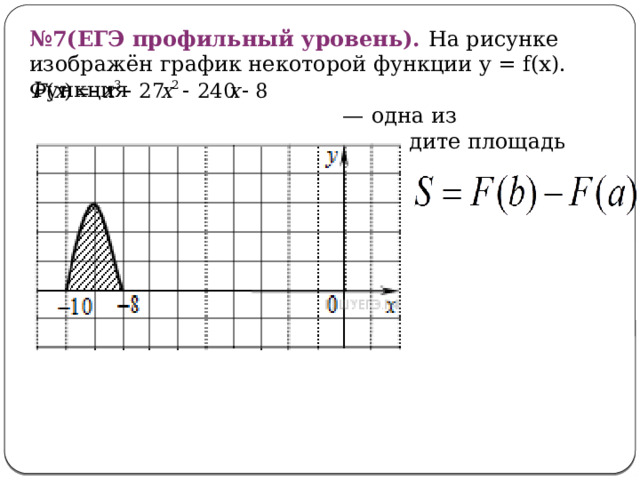
№ 7(ЕГЭ профильный уровень). На рисунке изображён график функции y = f(x). Функция
— одна из первообразных функции y = f(x). Найдите площадь закрашенной фигуры.
№ 7(ЕГЭ профильный уровень). На рисунке изображён график некоторой функции y = f(x). Функция
— одна из первообразных функции f(x). Найдите площадь закрашенной фигуры .

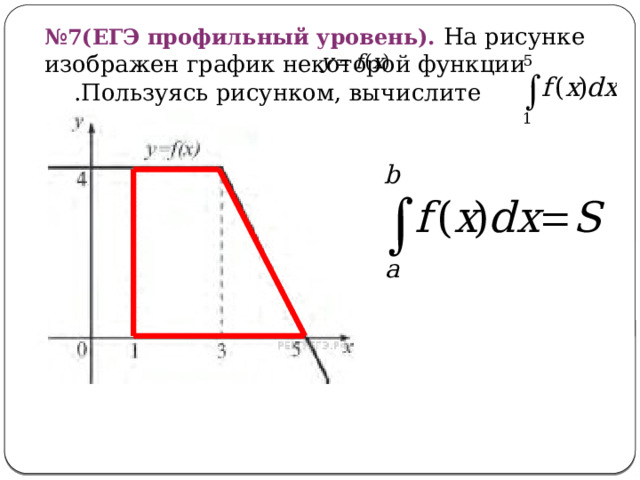
№ 7(ЕГЭ профильный уровень). На рисунке изображен график некоторой функции .Пользуясь рисунком, вычислите определенный интеграл









![№ 7(ЕГЭ профильный уровень). На рисунке изображён график функции y = F(x) — одной из первообразных функции f(x), определённой на интервале (−3; 5). Найдите количество решений уравнения f(x)=0 на отрезке [−2; 4]. 10](https://fsd.multiurok.ru/html/2021/03/20/s_6055c3baa9e9e/img3.jpg)



![Определенный интеграл В прямоугольной системе координат XOY фигура, ограниченная осью OX, прямыми , и графиком непрерывной неотрицательной на отрезке [ a;b ] функции , называется криволинейной трапецией](https://fsd.multiurok.ru/html/2021/03/20/s_6055c3baa9e9e/img7.jpg)
![Определенный интеграл Вычислим площадь криволинейной трапеции. который называют определенным интегралом от функции по отрезку [a;b] и обозначают так:](https://fsd.multiurok.ru/html/2021/03/20/s_6055c3baa9e9e/img8.jpg)

![Геометрический смысл определенного интеграла Площадь криволинейной трапеции, ограниченной графиком непрерывной положительной на промежутке [ a;b ] функции f(x) , осью x и прямыми x=a и x= b :](https://fsd.multiurok.ru/html/2021/03/20/s_6055c3baa9e9e/img10.jpg)

![Площадь фигуры, Ограниченной графиками непрерывных функций y=f(x) и y=g(x) таких, что для любого x из [a;b], где a и b – абсциссы точек пересечения графиков функций:](https://fsd.multiurok.ru/html/2021/03/20/s_6055c3baa9e9e/img12.jpg)














