Презентация к уроку "Площадь криволинейной трапеции"

Установка на успех

• В средние века жил английский ученый, которому нужно было точно вычислить площадь Англии. Он знал только точную площадь одного из графств и имел при себе карту Англии. Как вы думаете, каким способом этот ученый вычислил площадь своей страны?

Он вырезал контуры Англии и графства из карты и нашел отношение их весов. Точно в такой же пропорции соотносились и площади.

• Речь пойдет о площадях

3

2

2

2

0

2

0

2

0

3

2

0

2

2

0

Проблемный вопрос

• Какая фигура изображена на рисунке?

2

0

2

Тема урока

«Площадь криволинейной трапеции»

ПЛОЩАДЬ КРИВОЛИНЕЙНОЙ ТРАПЕЦИИ

15.02.2018

Проблемные вопросы

1

2

3

Ожидаемые результаты

1

2

3

Проверим, что знаем

2 1

3

4

Обработать деталь

Будут ли первообразными следующие функции

для функции

© Комаров Р.А.

Установить соответствие. Найти такой общий вид первообразной, которая соответствует заданной функции.

Проблемный вопрос

• Какая фигура изображена на рисунке?

2

0

2

х=а

x=b

,

Криволинейная трапеция

у

х

0

a

b

Определение: фигура, ограниченная графиком функции, непрерывной и не меняющей своего знака на отрезке [ a; b ], прямыми x=a, x=b и отрезком [ a; b ], называется криволинейной трапецией

Признаки понятия Криволинейная трапеция

• График непрерывной, не меняющей знак функции

у = f(x) на отрезке [ a ; b ] ;

• отрезки прямых x = a и

x = b ;

• отрезок [ a ; b ] лежит на оси Ох

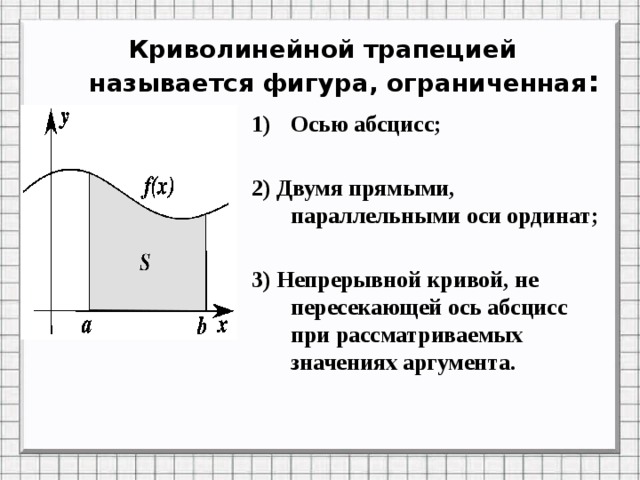
Криволинейной трапецией называется фигура, ограниченная :

• Осью абсцисс;

2) Двумя прямыми, параллельными оси ординат;

3) Непрерывной кривой, не пересекающей ось абсцисс при рассматриваемых значениях аргумента.

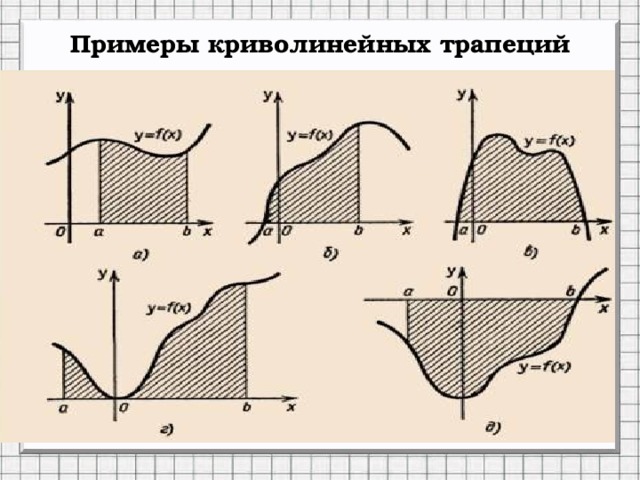
Примеры криволинейных трапеций

У=0,5х+1

Различные виды криволинейных трапеций

У=х²+2х

-1

-2

0

2

0

1

0

2

-1

-1

0

Различные виды криволинейных трапеций

Являются ли криволинейными трапециями фигуры?

у

у

у

y = f(x)

y = f(x)

3

y = f(x)

У=1

0

х

0

х

0

х

y = f(x)

у

у

у

y = f(x)

y = f(x)

У=3

Для проверки триггер – нажать на кнопку с № ответа (верно/неверно)

0

х

0

х

0

х

31

Проблемный вопрос

• Как найти площадь криволинейной трапеции ?

Взгляд на историю математики

Еще примерно в 370 году до нашей эры существовал метод нахождения площади криволинейной трапеции, изобретенный древнегреческим математиком Евдоксом Книдским. Данный способ назывался методом исчерпания Евдокса. Евдокс пытался найти площади, разрывая их на бесконечное число фигур, площади которых известны.

Способы вычисления площади

криволинейной трапеции

Метод прямоугольников

Метод прямоугольников

Чем больше количество частей, на которые разбивается отрезок [a;b], тем больше получается прямоугольников

и тем более точно вычисляется площадь криволинейной трапеции

n = 4

n = 9

31

Способы вычисления площади

криволинейной трапеции

Метод трапеций

Метод трапеций

Чем больше количество частей, на которые разбивается отрезок [a;b], тем больше получается трапеций

и тем более точно вычисляется площадь криволинейной трапеции

n = 4

n = 10

31

Способы вычисления площади

криволинейной трапеции

Метод трапеций

Метод прямоугольников

Также необходимо обратить внимание на то,

что Метод трапеций является более точным, чем Метод прямоугольников,

т.к. боковая (верхняя) сторона каждой маленькой трапеции почти совпадает с линией функции.

31

Теорема:

Если f – непрерывная и не меняет знак на отрезке [a; b] функция ,

а F – ее первообразная на этом отрезке , то площадь S соответствующей криволинейной трапеции равна приращению первообразной на отрезке [a; b] , т.е.

31

y=f(x)

Выберем между a и b на оси абсцисс фиксированную точку х и рассмотрим криволинейную трапецию , обозначим ее площадь через S(x).

y

S(x)

x

0

b

а

x

Каждому х из отрезка [a; b] соответствует вполне определенное значение S(x) , то есть S(x) можно назвать- функцией, зависящей от х.

х=а, то S(a)=0.

Если х=b , то S(b)=S (где S-площадь криволинейной трапеции).

© Комаров Р.А.

Алгоритм нахождения площади

криволинейной трапеции:

• Изобразить чертеж и убедиться, является ли данная фигура криволинейной трапецией
• Найти первообразную F(x)
• Применить формулу S=F(b)-F(a)

© Комаров Р.А.

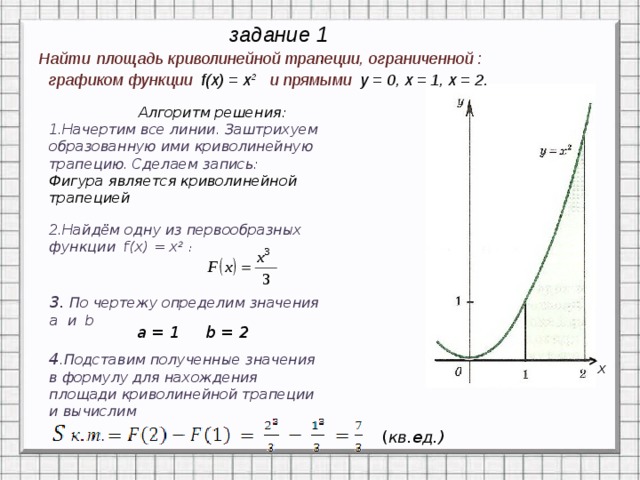
задание 1

Найти площадь криволинейной трапеции, ограниченной :

графиком функции f(x) = х 2 и прямыми у = 0, х = 1, х = 2.

,

Алгоритм решения:

1.Начертим все линии. Заштрихуем образованную ими криволинейную трапецию. Сделаем запись:

Фигура является криволинейной трапецией

2.Найдём одну из первообразных функции f(x) = х 2 :

3. По чертежу определим значения

a и b

a = 1 b = 2

4 .Подставим полученные значения в формулу для нахождения площади криволинейной трапеции и вычислим

х

( кв.ед.)

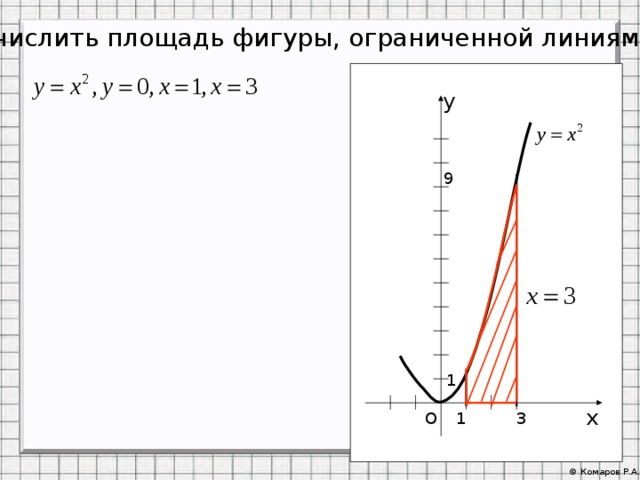
Вычислить площадь фигуры, ограниченной линиями

у

9

1

х

1

3

О

© Комаров Р.А.

Пример : Вычислить площадь криволинейной трапеции, ограниченной линиями

у = 4 - х² и у=0

41

Домашнее задание

• Найти площадь криволинейной трапеции, ограниченной линиями

1). f(x)=x 2 ,y=0, x=-1, x=2

2). f(x)=2x 2 -1 ,y=0, x=-1, x=3

3). f(x)=2x 2 +1 ,y=0, x=2, x=3