Презентация к уроку по теме: "Итоговое повторение курса геометрии"

8 класс

Итоговое повторение курса геометрии

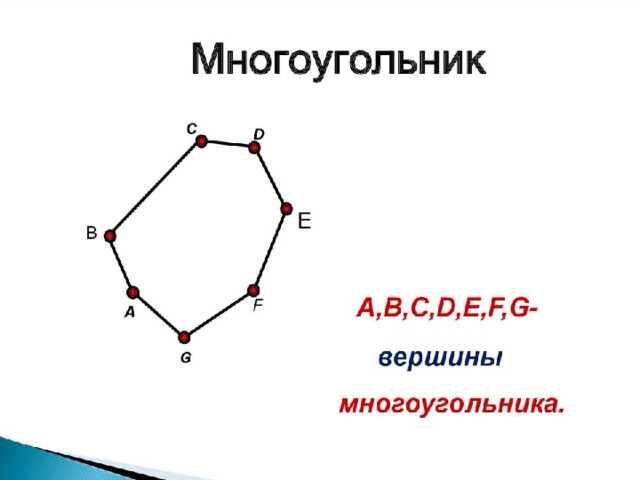
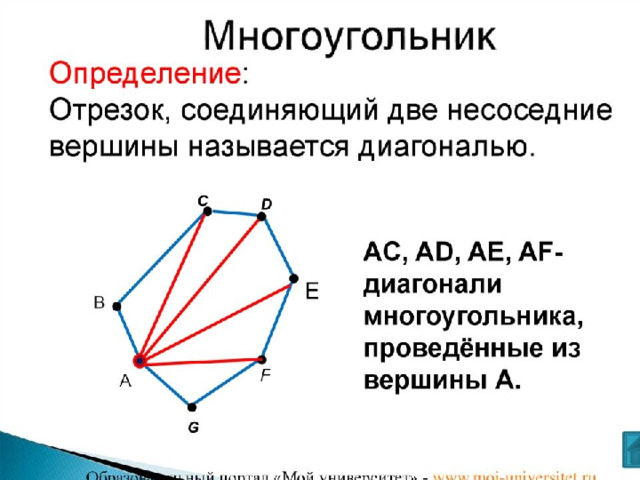
Задача

Сумма углов выпуклого многоугольника (п – 2)·180°

Сколько сторон имеет многоугольник, если каждый угол

которого равен 120°.

Решение

Обозначим п – количество вершин многоугольника.

Так как сумма углов выпуклого многоугольника

(п – 2) · 180°.

То следовательно (п – 2) · 180° = 120° · п

180° · п - 360° = 120° · п

60° · п = 360°

п = 360° : 60°

п = 6

Ответ: 6 сторон.

30.11.2012

www.konspekturoka.ru

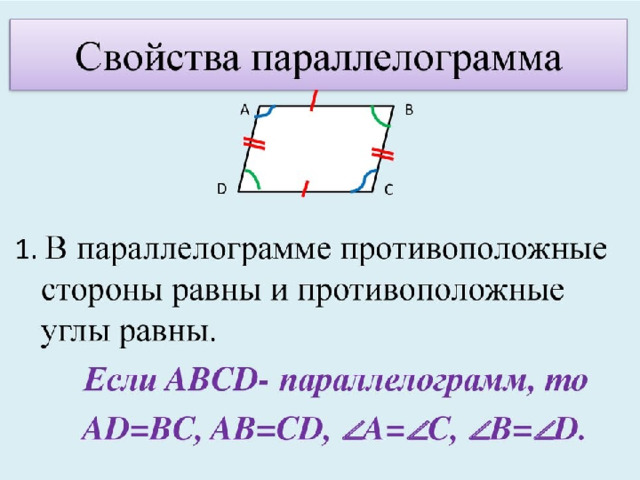
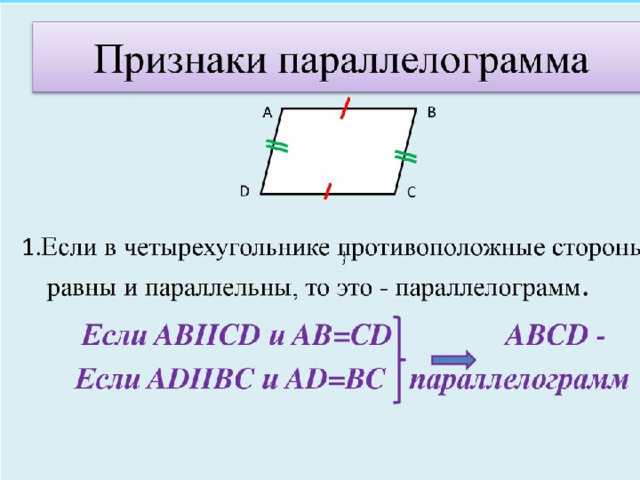
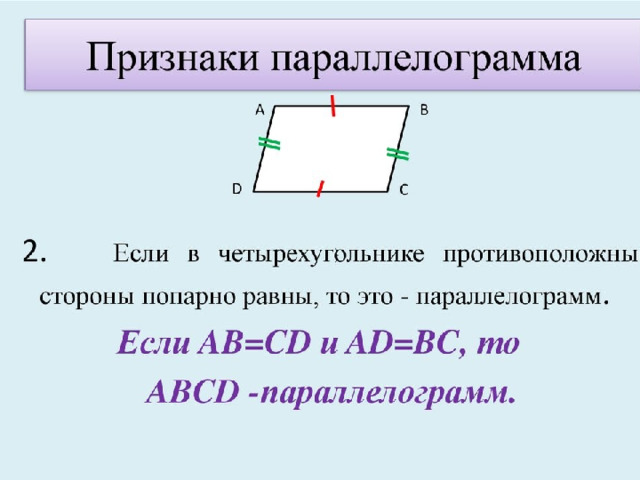
Параллелограмм

Прямоугольник

Ромб

Квадрат

Трапеция

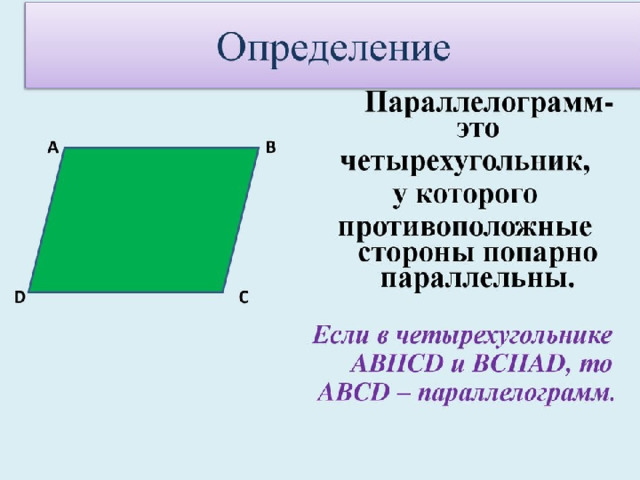
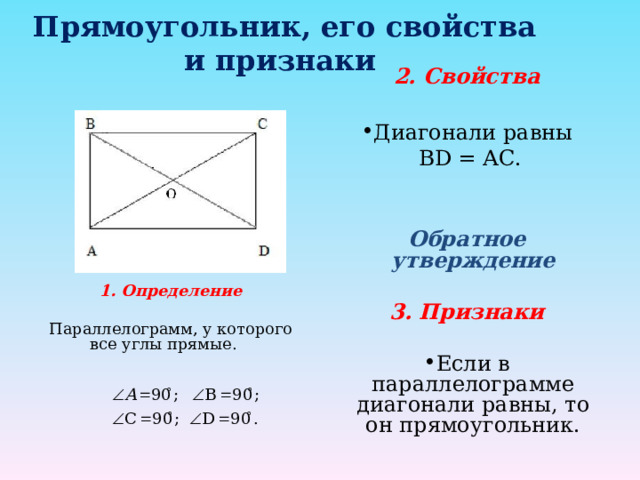
Прямоугольник, его свойства и признаки

2. Свойства

• Диагонали равны

BD = AC.

Обратное утверждение

3. Признаки

• Если в параллелограмме диагонали равны, то он прямоугольник.

1. Определение

Параллелограмм, у которого все углы прямые.

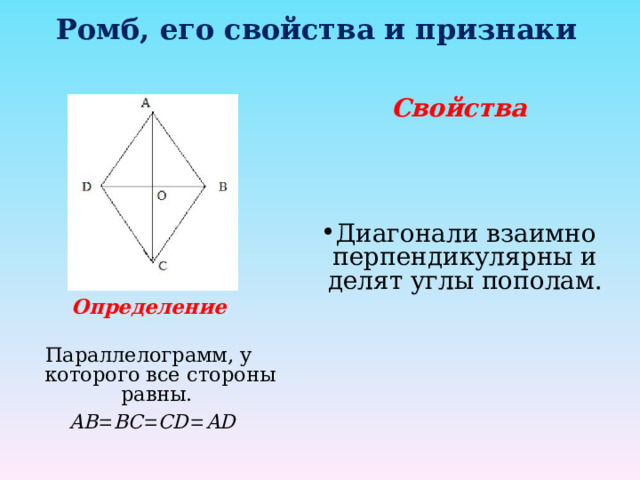
Ромб, его свойства и признаки

Свойства

• Диагонали взаимно перпендикулярны и делят углы пополам.

Определение

Параллелограмм, у которого все стороны равны.

Квадрат, его свойства и признаки

Свойства

• Диагонали равны, взаимно перпендикулярны , точкой пересечения делятся пополам и делят углы пополам.

• Признаки
• Если в ромбе все углы равны, то он квадрат.

• Если в ромбе диагонали равны, то он квадрат.

Определение

Прямоугольник, у которого все стороны равны.

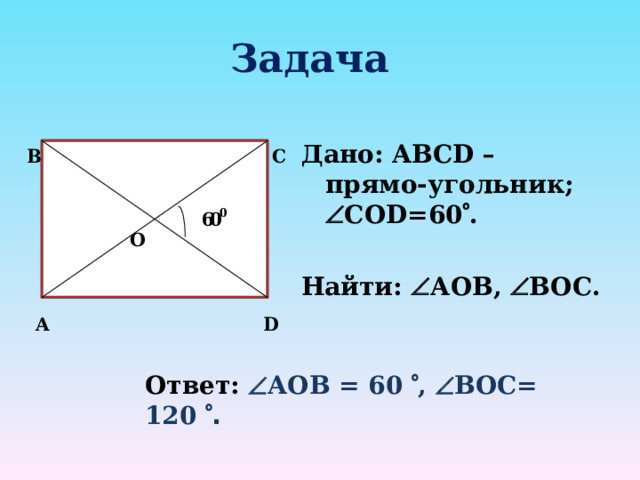
Задача

Дано: ABCD – прямо - угольник;  C О D = 60  .

Найти:  А OB ,  BOC .

В C

60 0

Ответ:  А OB = 60  ,  BOC = 120  .

Задача

Дано: ABCD – прямоугольник;

 ABD больше  СВ D на 20°.

Найти: углы треугольника АО D .

Ответ:  А = 35  ,  O = 1 1 0  ,  D = 35 

Задача

В ромбе угол между диагональю и стороной равен 25  . Найдите углы ромба.

Ответ: 50°; 130°

Теорема Пифагора

В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

Это простота - красота - значимость

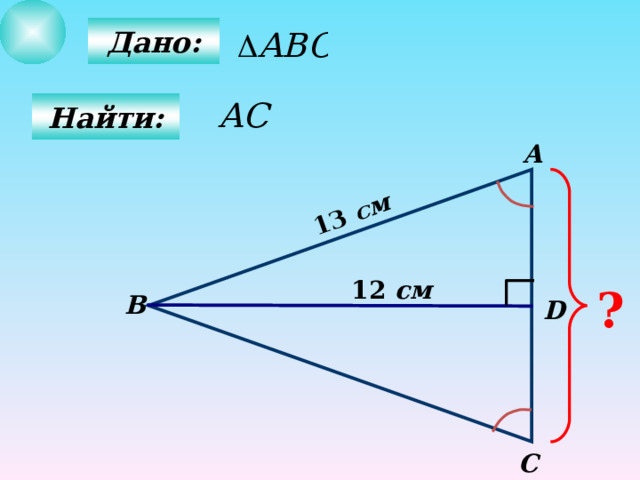
13 см

Дано:

Найти:

А

12 см

?

B

D

C

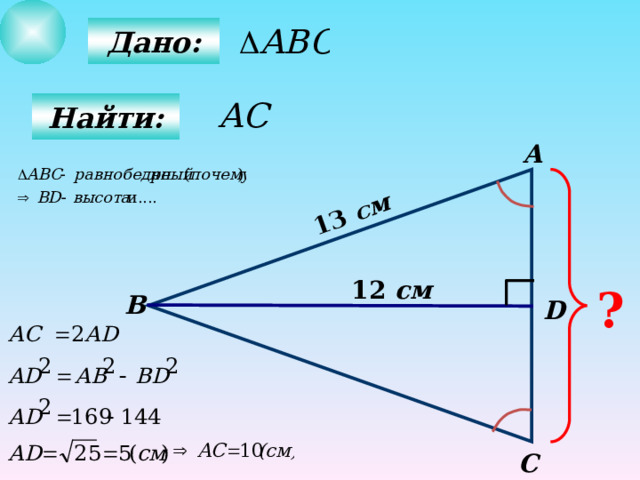
13 см

Дано:

Найти:

А

12 см

?

B

D

C

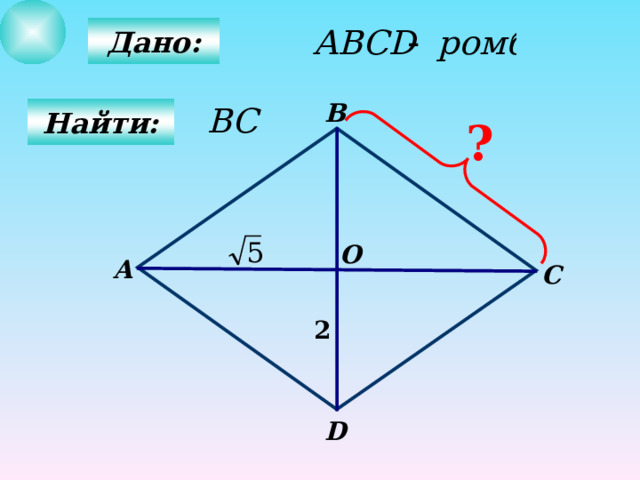
Дано:

В

Найти:

?

О

А

С

2

D

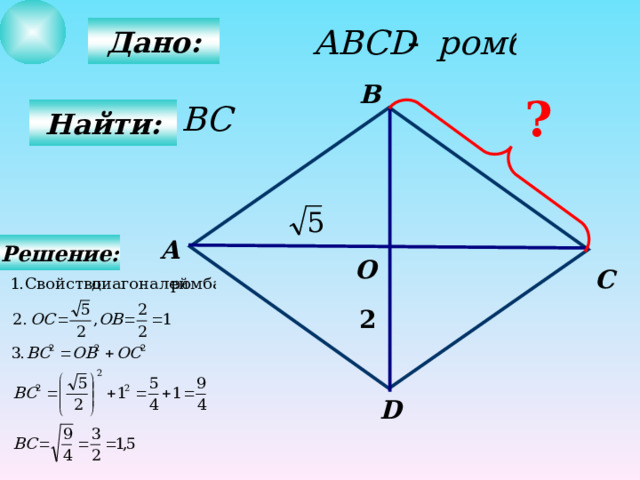
Дано:

В

?

Найти:

А

Решение:

О

С

2

D

Первый признак подобия треугольников

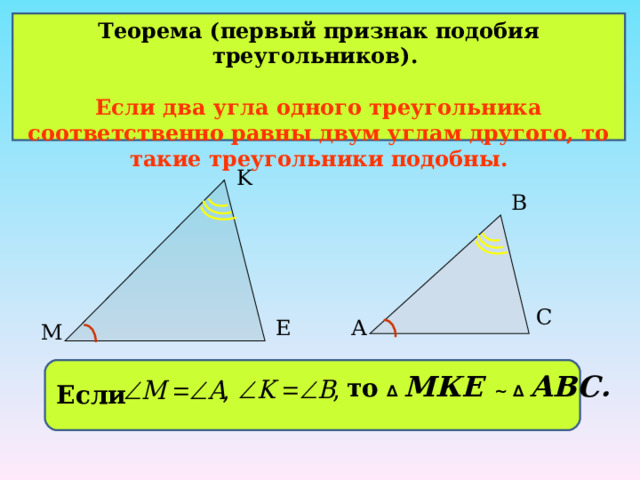
Теорема ( первый признак подобия треугольников ) .

Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.

K

В

С

А

E

M

то ∆ МКЕ ~ ∆ АВС.

Если

№

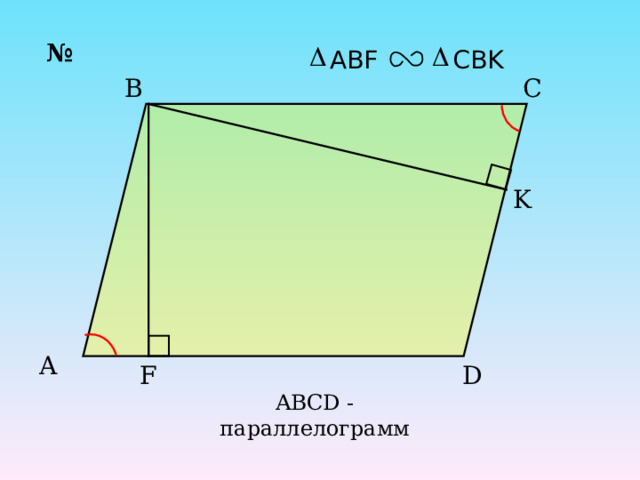
CBK

ABF

B

C

K

A

D

F

ABCD - параллелограмм

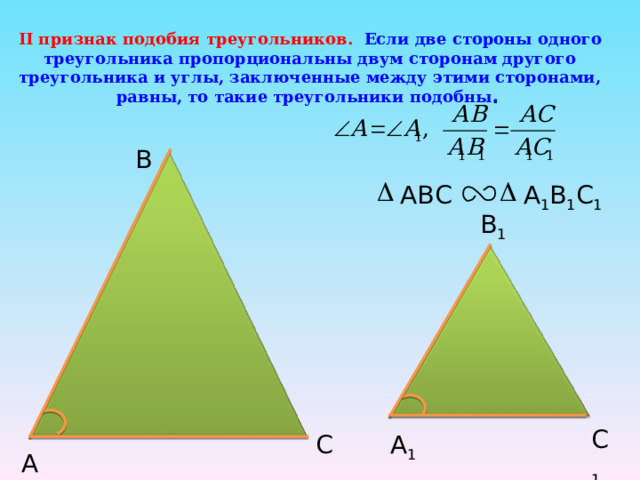
II признак подобия треугольников. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны .

B

ABC

А 1 В 1 С 1

B 1

C 1

C

А 1

А

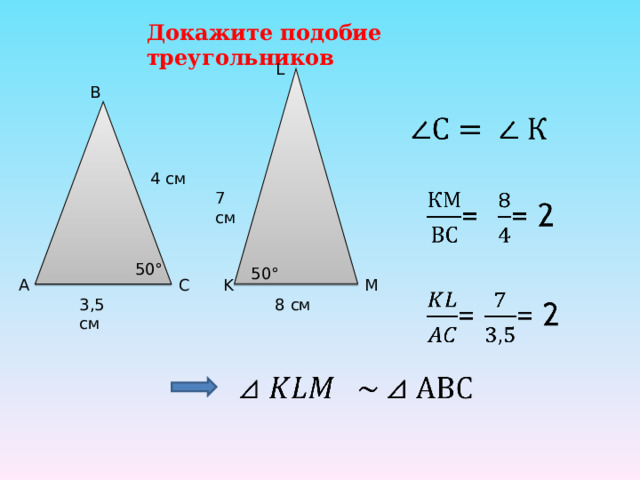
Докажите подобие треугольников

L

В

4 см

7 см

50°

50°

С

K

А

M

8 см

3,5 см

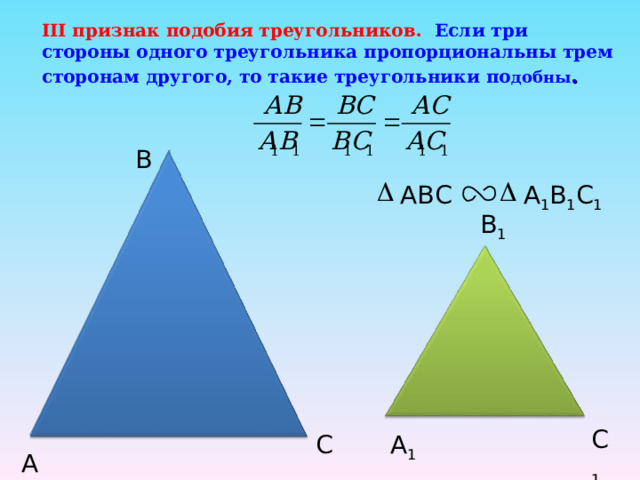
III признак подобия треугольников. Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники по добны .

B

ABC

А 1 В 1 С 1

B 1

C 1

А 1

C

А

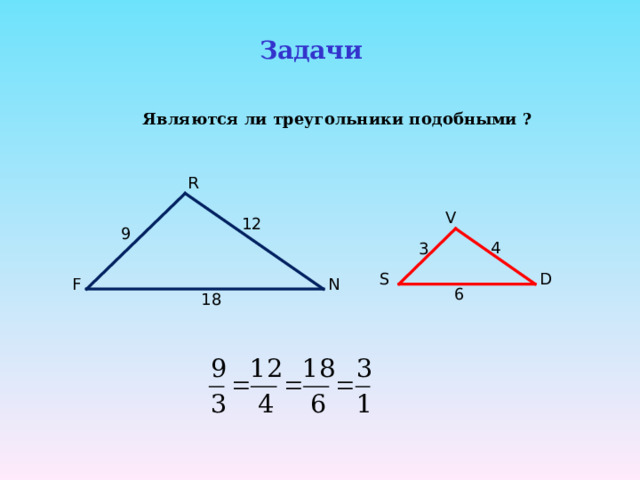
Задачи

Являются ли треугольники подобными ?

R

V

12

9

4

3

S

D

N

F

6

18

ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ И ОКРУЖНОСТИ

Свойство касательной : Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.

M

m – касательная к окружности с центром О

М – точка касания

OM - радиус

m

O

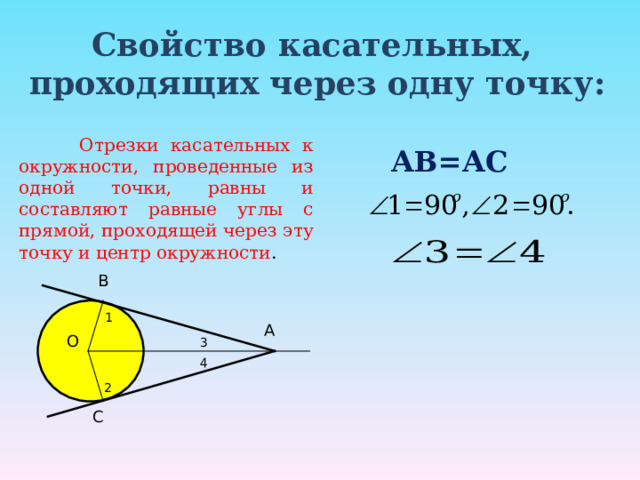
Свойство касательных, проходящих через одну точку:

Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности .

АВ=АС

В

1

А

О

3

4

2

С

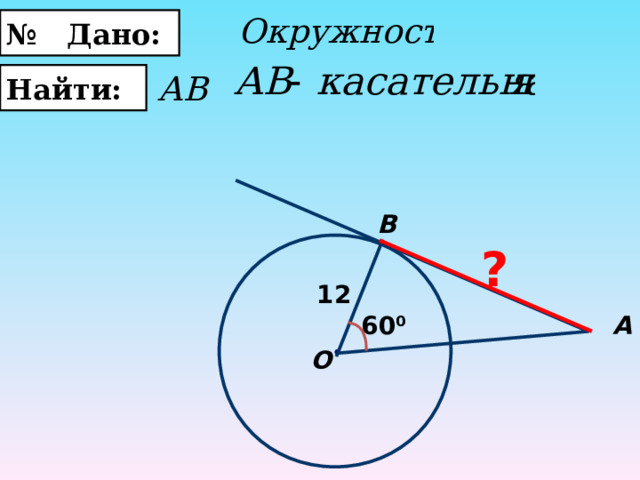
№ Дано:

Найти:

B

?

12

А

60 0

О

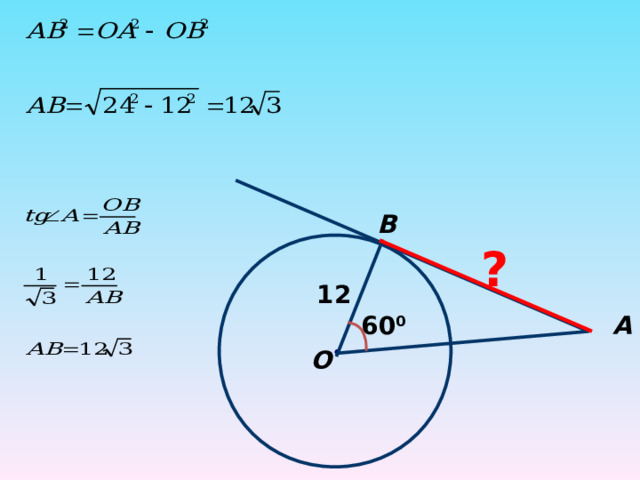
B

?

12

А

60 0

О

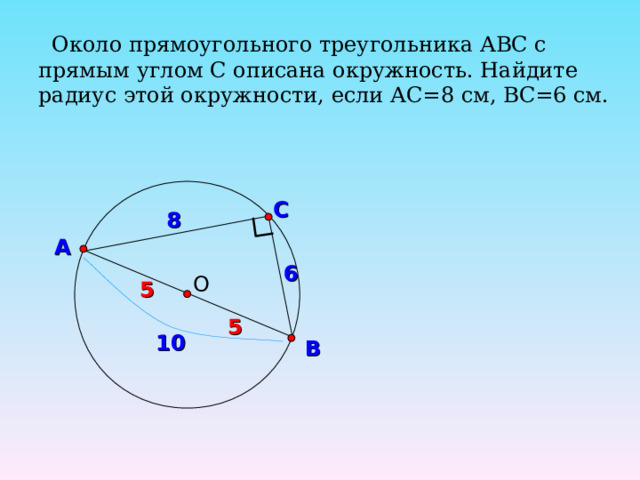
Около прямоугольного треугольника АВС с прямым углом С описана окружность. Найдите радиус этой окружности, если АС=8 см, ВС=6 см.

С

8

А

6

О

5

5

10

В

39

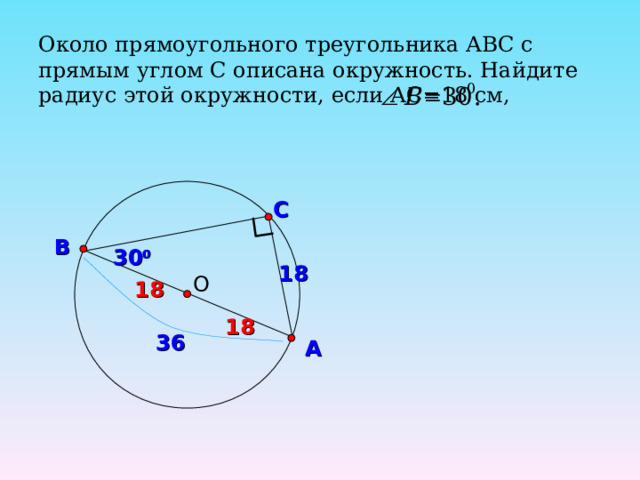
Около прямоугольного треугольника АВС с прямым углом С описана окружность. Найдите радиус этой окружности, если АС=18 см,

С

В

30 0

18

О

18

18

36

А

40

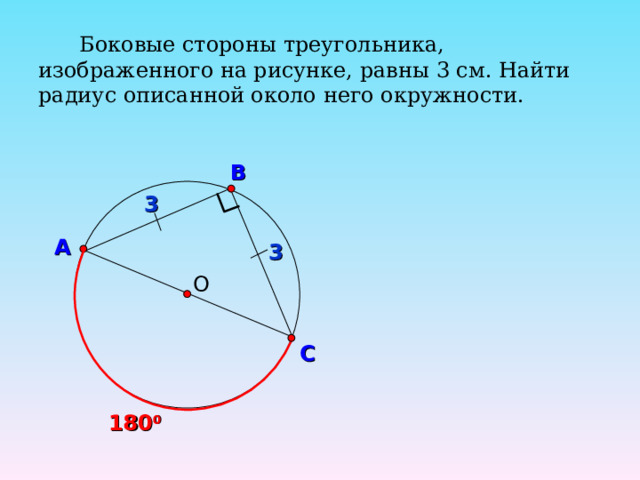
Боковые стороны треугольника, изображенного на рисунке, равны 3 см. Найти радиус описанной около него окружности.

В

3

А

3

О

Тесты. Геометрия 9 класс. Варианты и ответы централизованного (итогового) тестирования – М.: Центр тестирования МО РФ, 2003.

С

180 0

40

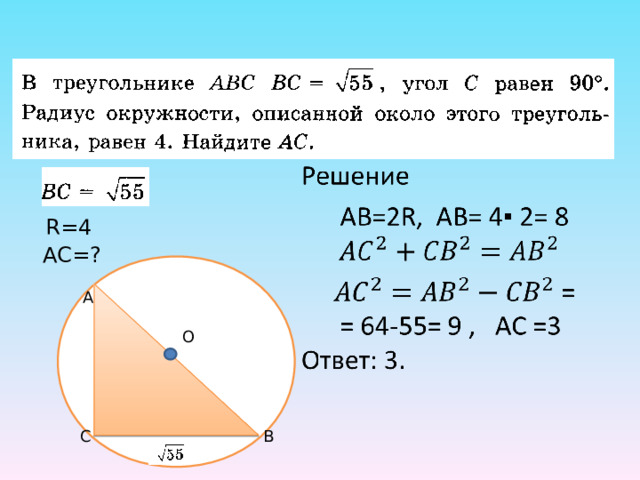
R=4

AC= ?

A

O

B

C

№

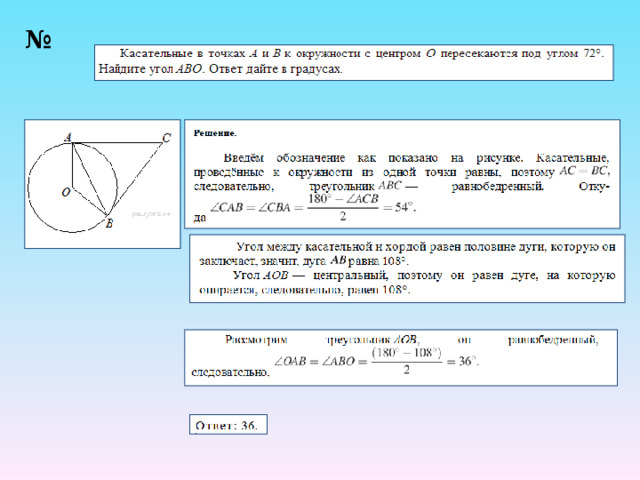
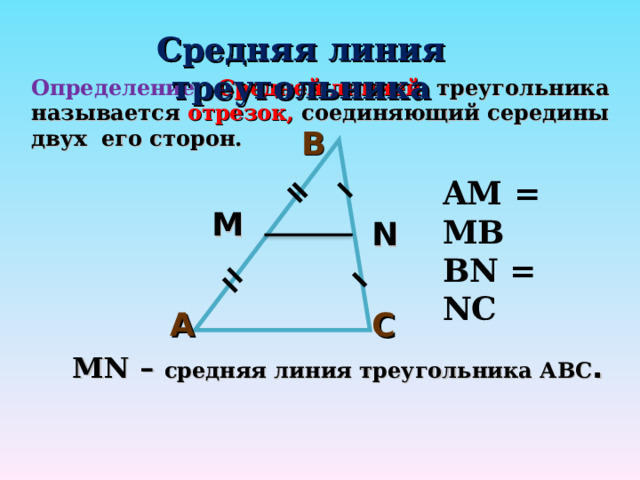
Средняя линия треугольника

Определение: Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.

В

AM = MB

BN = NC

М

N

С

А

М N – средняя линия треугольника АВС .

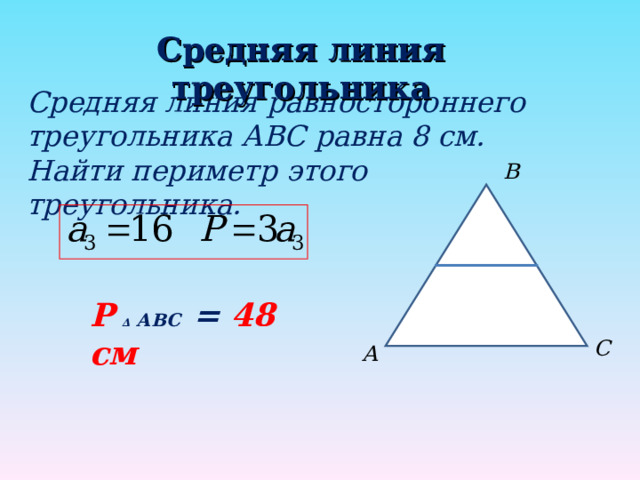
Средняя линия треугольника

Средняя линия равностороннего треугольника АВС равна 8 см. Найти периметр этого треугольника.

В

Р ∆ АВС = 48 см

С

А