Презентация по теме "Треугольники"

Обобщающее повторение по теме: Треугольники

Урок геометрии в 10 классе

Раздел: Повторение планиметрии

Содержание

• Вводное повторение
• Сумма углов треугольника
• Свойства равнобедренного треугольника
• Замечательные линии в треугольнике
• Вписанная и описанная окружности
• Свойства четырех замечательных точек

треугольника

• Теорема Пифагора
• Площадь треугольника

Вспомните:

• Какая фигура называется треугольником? Какими могут быть треугольники в зависимости от величины углов? Какой треугольник называется прямоугольным ? Как называются стороны прямоугольного треугольника? Какой треугольник называется тупоугольным ? Может ли в треугольнике быть два тупых угла? Какой угол называется внешним углом треугольника? Каким свойством обладает внешний угол треугольника? Сформулировать теорему о сумме углов треугольника.
• Какая фигура называется треугольником?
• Какими могут быть треугольники в зависимости от величины углов?
• Какой треугольник называется прямоугольным ?
• Как называются стороны прямоугольного треугольника?
• Какой треугольник называется тупоугольным ?
• Может ли в треугольнике быть два тупых угла?
• Какой угол называется внешним углом треугольника?
• Каким свойством обладает внешний угол треугольника?
• Сформулировать теорему о сумме углов треугольника.

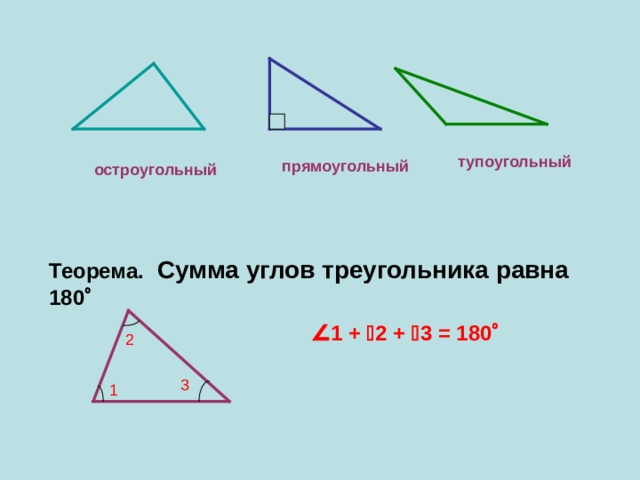
тупоугольный

прямоугольный

остроугольный

Теорема. Сумма углов треугольника равна 180 

 1 +  2 +  3 = 180 

2

3

1

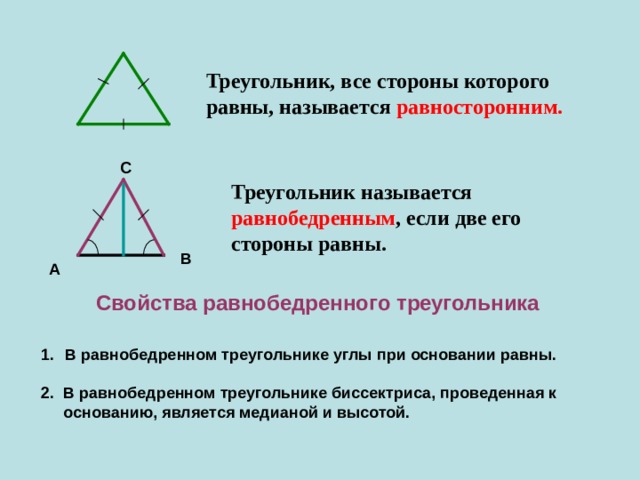
Треугольник, все стороны которого

равны, называется равносторонним.

C

Треугольник называется

равнобедренным , если две его

стороны равны.

B

А

Свойства равнобедренного треугольника

• В равнобедренном треугольнике углы при основании равны.

2. В равнобедренном треугольнике биссектриса, проведенная к

основанию, является медианой и высотой.

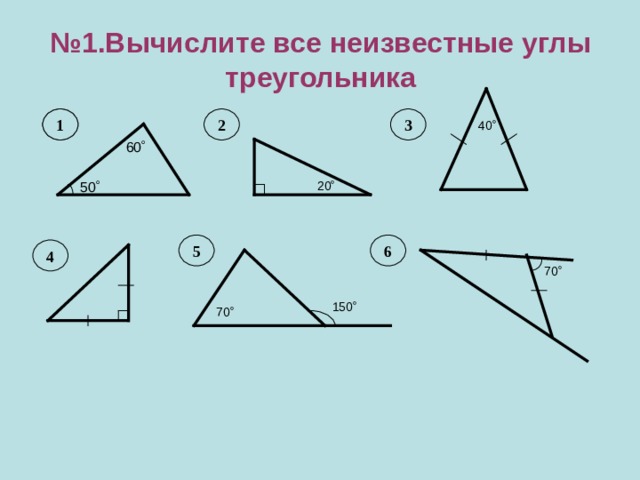
№ 1.Вычислите все неизвестные углы треугольника

2

1

3

1

40 

60 

20 

50 

5

6

4

70 

150 

70 

Замечательные линии в треугольнике

• медиана
• биссектриса
• высота

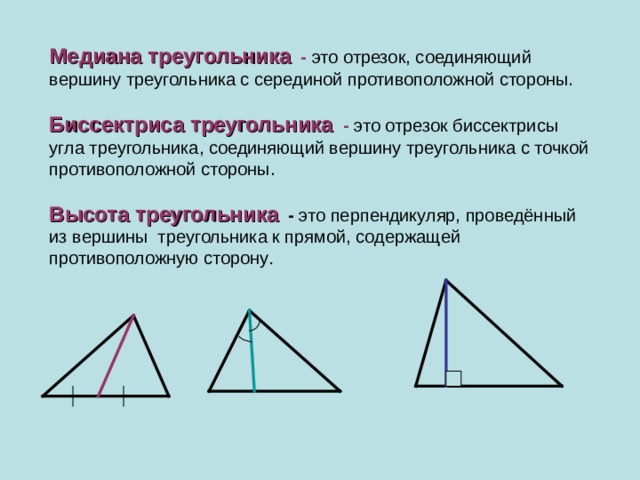
Медиана треугольника - это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

Биссектриса треугольника - это отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.

Высота треугольника - это перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону .

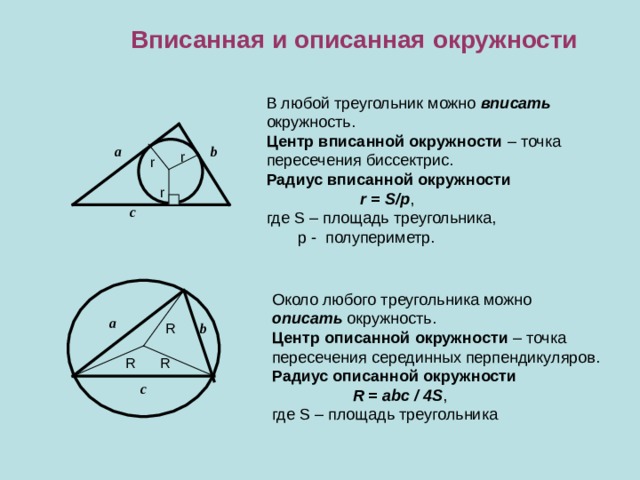
Вписанная и описанная окружности

В любой треугольник можно вписать

окружность.

Центр вписанной окружности – точка

пересечения биссектрис.

Радиус вписанной окружности

r = S/p ,

где S – площадь треугольника,

p - полупериметр.

a

b

r

r

r

c

Около любого треугольника можно

описать окружность.

Центр описанной окружности – точка

пересечения серединных перпендикуляров.

Радиус описанной окружности

R = abc / 4S ,

где S – площадь треугольника

a

R

b

R

R

c

При решении задач, связанных с треугольником, нередко используются свойства четырёх замечательных точек треугольника :

Три медианы треугольника пересекаются в одной точке, лежащей строго внутри треугольника (центр тяжести). Точка пересечения делит медианы на отрезки, длины которых относятся как 2:1, считая от соответствующей вершины.

Три биссектрисы треугольника пересекаются в одной точке, лежащей строго внутри треугольника. Точка пересечения биссектрис равноудалена от сторон треугольника (центр вписанной окружности).

Три перпендикуляра, проведённые к серединам сторон треугольника, пересекаются в одной точке. Эта точка равноудалена от вершин треугольника и является центром описанной окружности.

Три высоты треугольника пересекаются в одной точке (ортоцентр).

Историческая справка ПИФАГОР САМОССКИЙ (ок. 580 – ок. 500 г. до н.э.)

Великий древнегреческиий ученый Пифагор родился на острове Самос в VI в. до н.э.

Геометрия достигла высокого развития в Древней Греции в школе Пифагора .

Теорема Пифагора

квадрат гипотенузы прямоугольного треугольника равен сумме квадратов его катетов.

c 2  =  a 2  +  b 2

а 2  =  с 2  -  b 2

в 2  =  с 2  -  а 2

№ 2. Задачи по чертежу:

Установите, под каким номером находится верно записанная

запись теоремы Пифагора для данных треугольников:

1

a

a

c

b

1

3

a

c

2

c

b

b

1) а 2 =b 2 +c 2 2) c 2 =a 2 +b 2 3) a 2 =c 2 +b 2

№ 2 . Найдите х:

х

2

2

3

4

4

 2

3

45 

х

х

135 

5

1

6

5

х

6

10

4

8

х

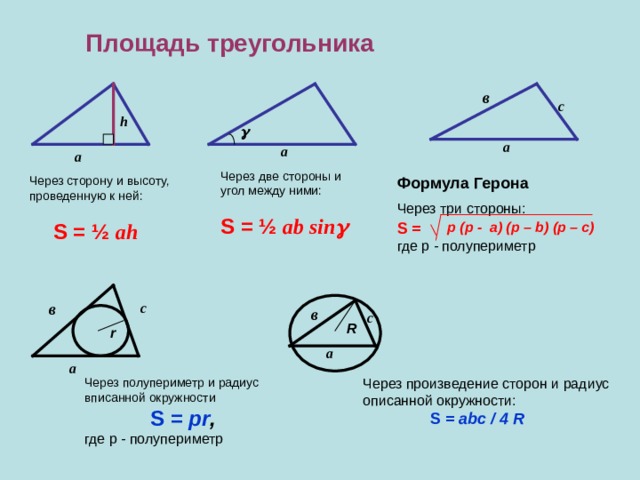
Площадь треугольника

в

с

h



а

а

а

Через две стороны и угол между ними:

S = ½ а b sin 

Формула Герона

Через три стороны:

Через сторону и высоту, проведенную к ней:

S = ½ а h

S =

где p - полупериметр

p ( p - a) (p – b) (p – c)

в

с

в

с

R

r

а

а

Через полупериметр и радиус

вписанной окружности

S = pr ,

где p - полупериметр

Через произведение сторон и радиус

описанной окружности:

S = а b с / 4 R

№ 3. Вычислите площадь треугольника

1

2

8

5

6

30 

15

9

4

3

1 0

6

6

Проверь себя. Лист самооценки учащегося к уроку геометрии по теме «Треугольники»

№ 1

1

ответ

2

70 

3

70 

4

70  , 70 

5

45  , 45 

6

8 0 

110  ,35  , 35 

№ 2

ответ

1

1)

2

5

3

1

4

5

5

5

6

6

№ 3

ответ

1

2

30

10  2

3

24

4

9  3

Критерии оценки

• За каждый верный ответ – 1 балл
• Исправления не принимаются, считаются ошибкой.
• Если вы набрали

15 – 16 баллов - оценка « 5 »

11 – 14 баллов - оценка « 4 »

6 – 10 баллов - оценка « 3 »

Поставьте себе оценку за урок.

Задание на дом:

• Учебник Геометрия 7-9 Атанасян Л.С. и др.

стр. 133 № 492, стр. 135 № 515

• Подготовка к уроку семинару:

глава XI §1-2 - повторить (всем)

Индивидуальные задания.

Спасибо за урок!

Литература

• Атанасян Л.С. Геометрия 7-9. – М.: Просвещение, 2006
• Саврасова С.М., Ястребинецкий Г.А. Упражнения по планиметрии на готовых чертежах: Пособие для учителя. – М.: Просвещение, 1987
• Генденштейн Л.Э., Ершова А.П. Наглядный справочник по геометрии для 7-11 классов – Москва – Харьков: Научно – методический центр «Развивающее обучение», 1996