Презентация по теме "треугольники"

Виды и свойства треугольников

В

С

А

Цели и задачи урока

• Повторить и обобщить знания о треугольниках

их видах и свойствах.

• Закрепить умения и навыки решения типовых задач

по данной теме.

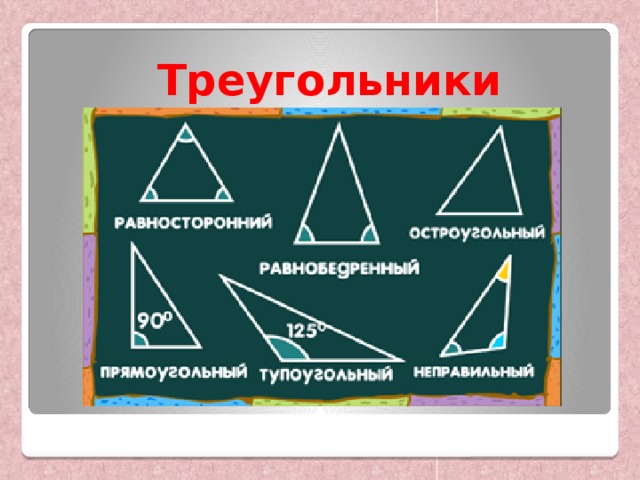
Треугольники

Виды треугольников

По сторонам

Равнобедренный

Равносторонний

Разносторонний

Виды треугольников

По углам

Остроугольный

Тупоугольный

Прямоугольный

Определите вид треугольника

Отрезки в треугольнике

Н

М

к

В

Если L MKO= 90 ° , то …

С

А

R

Н

О

Е

Если AH=HR, то …

Если L CDE= L TDE, то …

Т

D

Какие отрезки проведены ?

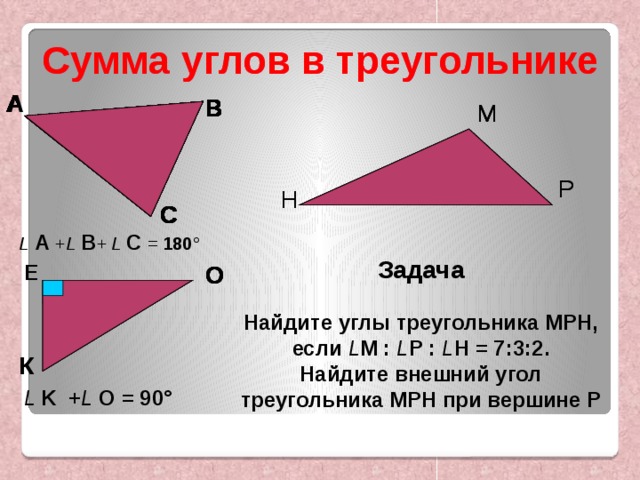
Сумма углов в треугольнике

Сумма углов в треугольнике

А

А

А

А

А

А

А

А

А

В

В

В

В

В

В

В

В

М

М

М

Р

Р

Н

Н

Н

Н

С

С

С

С

С

С

L А + L В + L С = 180 °

Задача

Найдите углы треугольника МРН, если L M : L Р : L Н = 7:3:2.

Найдите внешний угол треугольника МРН при вершине Р

Е

О

Е

Е

О

Е

О

К

К

L K + L O = 90 °

Равнобедренный треугольник

Задача

Сумма двух сторон равнобедренного треугольника

равна 26см,а его периметр равен 36см. Какими могут быть стороны этого треугольника?

Признаки равенства треугольников

В треугольнике выделяют шесть основных элементов – три внутренних угла и три соответственно противолежащие им стороны.

Равенство треугольников устанавливается

по равенству трех элементов:

1) двум сторонам и углу между ними;

2) по стороне и прилежащим к ней углам;

3) по трём сторонам.

Первый признак равенства треугольников

(по двум сторонам и углу между ними).

Если две стороны и угол между ними одного треугольника

равны соответственно двум сторонам и углу между ними

другого треугольника, то такие треугольники равны.

Если в треугольниках ∆ АВС и ∆ А 1 В 1 С 1

АВ = А 1 В 1 ; АС = А 1 С 1 ; ے А = ے А 1 ,

то ∆ АВС = ∆ А 1 В 1 С 1

Решение задач

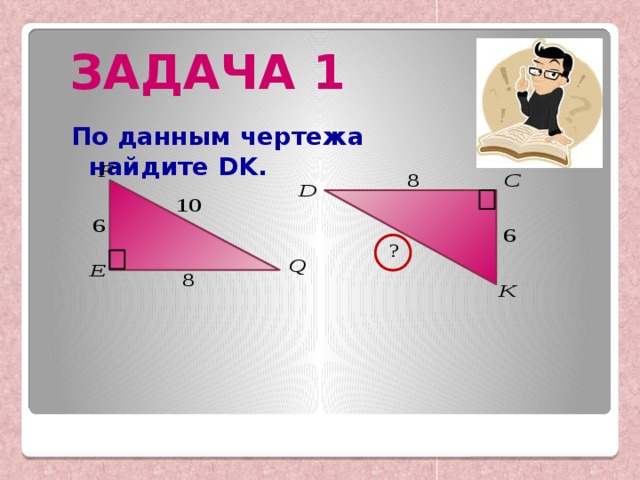
ЗАДАЧА 1

По данным чертежа найдите DK.

ЗАДАЧА 2

AD – биссектриса угла А;

АВ = АС.

Докажите: BD = CD.

ЗАДАЧА 3

Дано: B С = DA; ے BCА = ے DAC.

Докажите: ے АBC = ے CDA.

Теорема: Если сторона и два прилегающих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

А 1

В 1

С 1

А

В

С

ЕСЛИ В  ABC и  A 1 B 1 C 1 АВ = A 1 B 1 A = A 1 B= B 1 ТО  ABC=  A 1 B 1 C 1

19

Решение задач

ЗАДАЧА 1

С

В

Доказать равенство

 AВС и  CDA

А

D

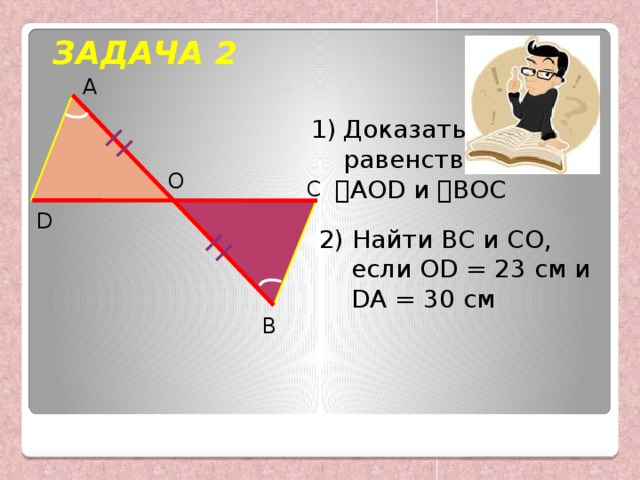
ЗАДАЧА 2

А

• Доказать равенство:

 AOD и  BОC

О

С

D

2) Найти ВС и СО, если ОD = 23 см и DA = 30 см

В

ЗАДАЧА 3

• Доказать равенство

 ТСО и  РВО

Т

2) Найти ОС и ТС, если ОВ = 5 дм и ВР = 30 см

О

В

С

Р

Третий признак равенства треугольников

Теорема: Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника то такие треугольники равны

Если в ∆ ABC и ∆ A 1 B 1 C 1 ;

AB = A 1 B 1 ; BC = B 1 C 1 ;AC = A 1 C 1,

то: ∆ ABC = ∆ A 1 B 1 C 1 .

B

А

C

B 1

C 1

A 1

Решение задач (устно)

Найди пары равных треугольников и доказать их равенство.

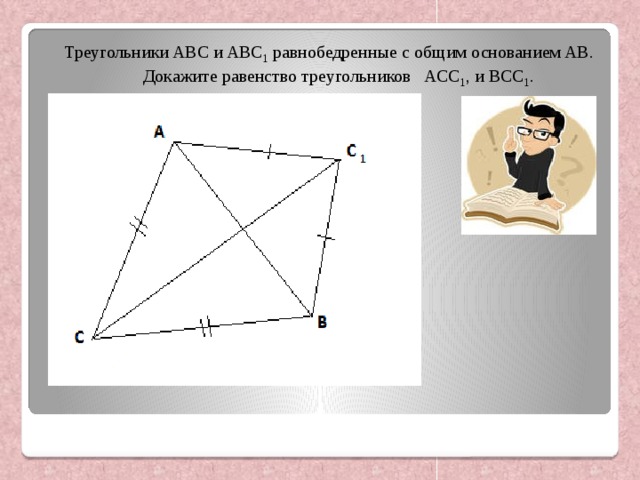
Треугольники ABC и ABC 1 равнобедренные с общим основанием AB. Докажите равенство треугольников ACC 1 , и BCC 1 .

Прямоугольный

треугольник

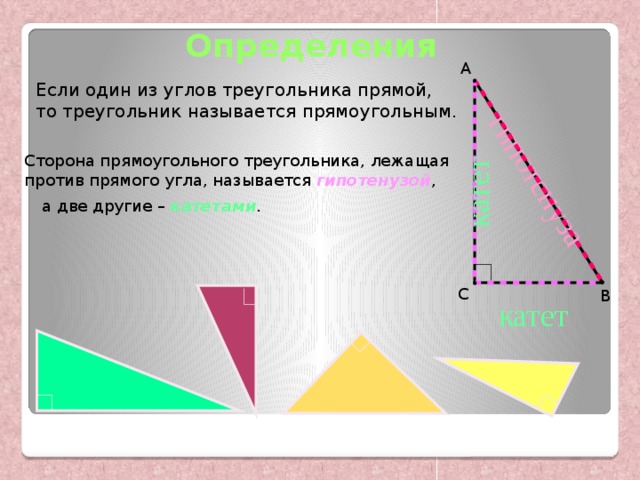
гипотенуза

катет

Определения

А

Если один из углов треугольника прямой,

то треугольник называется прямоугольным.

Сторона прямоугольного треугольника, лежащая

против прямого угла, называется гипотенузой ,

а две другие – катетами .

С

В

катет

Из истории математики

Прямоугольный треугольник занимает почётное место в вавилонской геометрии, упоминание о нём часто встречается в папирусе Ахмеса .

Термин гипотенуза происходит от греческого hypoteinsa ,

означающего тянущаяся под чем либо , стягивающая .

Слово берёт начало от образа древнеегипетских арф, на которых струны

натягивались на концы двух взаимно перпендикулярных подставок.

Термин катет происходит от греческого слова « катетос »,

которое означало отвес , перпендикуляр . В средние века словом катет

означали высоту прямоугольного треугольника, в то время, как другие его

стороны называли гипотенузой, соответственно основанием.

В XVII веке слово катет начинает применяться в современном смысле и

широко распространяется, начиная с XVIII века.

Евклид употребляет выражения:

«стороны, заключающие прямой угол», - для катетов;

«сторона, стягивающая прямой угол», - для гипотенузы.

Некоторые свойства

прямоугольных треугольников

1. Сумма двух острых углов прямоугольного треугольника равна 90 0 .

2. Катет прямоугольного треугольника, лежащий против угла в 30 0 ,

равен половине гипотенузы.

3. Если катет прямоугольного треугольника равен половине гипотенузы,

то угол, лежащий против этого катета, равен 30 0 .

Признаки равенства

прямоугольных треугольников

• Если катеты одного прямоугольного треугольника

соответственно равны катетам другого, то такие треугольники равны.

2. Если катет и прилежащий к нему острый угол одного прямоугольного

треугольника соответственно равны катету и прилежащему к нему углу

другого, то такие треугольники равны.

3. Если гипотенуза и острый угол одного прямоугольного треугольника

соответственно равны гипотенузе и острому углу другого,

то такие треугольники равны.

4. Если гипотенуза и катет одного прямоугольного треугольника

соответственно равны гипотенузе и катету другого,

то такие треугольники равны.

Признаки равенства

прямоугольных треугольников

• Если катеты одного прямоугольного треугольника

соответственно равны катетам другого, то такие треугольники равны.

2. Если катет и прилежащий к нему острый угол одного прямоугольного

треугольника соответственно равны катету и прилежащему к нему углу

другого, то такие треугольники равны.

3. Если гипотенуза и острый угол одного прямоугольного треугольника

соответственно равны гипотенузе и острому углу другого,

то такие треугольники равны.

4. Если гипотенуза и катет одного прямоугольного треугольника

соответственно равны гипотенузе и катету другого,

то такие треугольники равны.

15 см

4,2 см

Задачи по готовым чертежам

В

А

В

37 0

?

?

30 0

С

А

?

А

70 0

С

С

В

D

В

С

?

?

?

120 0

А

В

D

8,4 см

С

А

4 см

Контрольный тест

1. Прямоугольным называется треугольник, у которого

а) все углы прямые;

б) два угла прямые;

в) один прямой угол.

Контрольный тест

2. В прямоугольном треугольнике всегда

а) два угла острых и один прямой;

б) один острый угол, один прямой и один тупой угол;

в) все углы прямые.

Контрольный тест

3. Стороны прямоугольного треугольника, образующие

прямой угол, называются

а) сторонами треугольника;

б) катетами треугольника;

в) гипотенузами треугольника.

Контрольный тест

4. Сторона прямоугольного треугольника, противолежащая прямому углу, называется

а) стороной треугольника;

б) катетом треугольника;

в) гипотенузой треугольника.

Контрольный тест

5. Сумма острых углов прямоугольного треугольника

равна

а) 180 °;

б) 100°;

в) 90°.

Спасибо за внимание!