
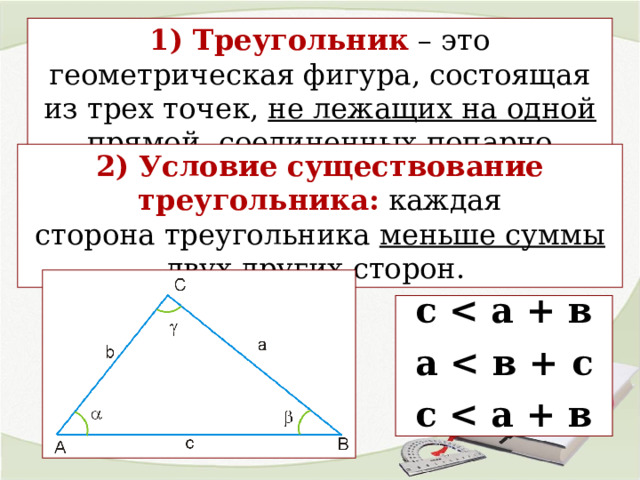
1) Треугольник – это геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой , соединенных попарно отрезками.
2) Условие существование треугольника: каждая сторона треугольника меньше суммы двух других сторон.
с а + в
а в + с
с а + в
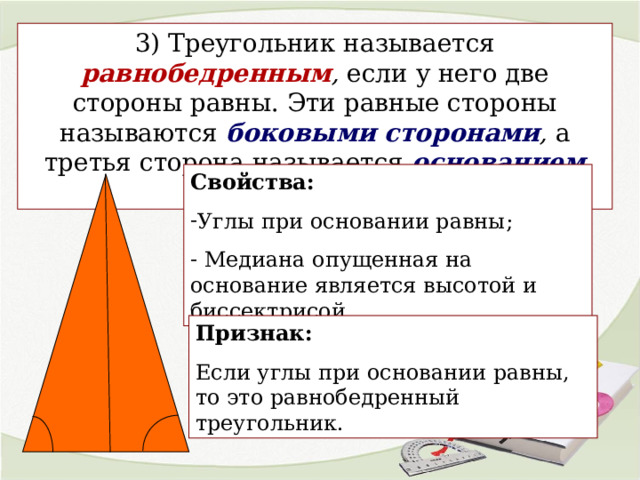
3) Треугольник называется равнобедренным , если у него две стороны равны. Эти равные стороны называются боковыми сторонами , а третья сторона называется основанием треугольника.
Свойства:
- Углы при основании равны;
- Медиана опущенная на основание является высотой и биссектрисой.
Признак:
Если углы при основании равны, то это равнобедренный треугольник.
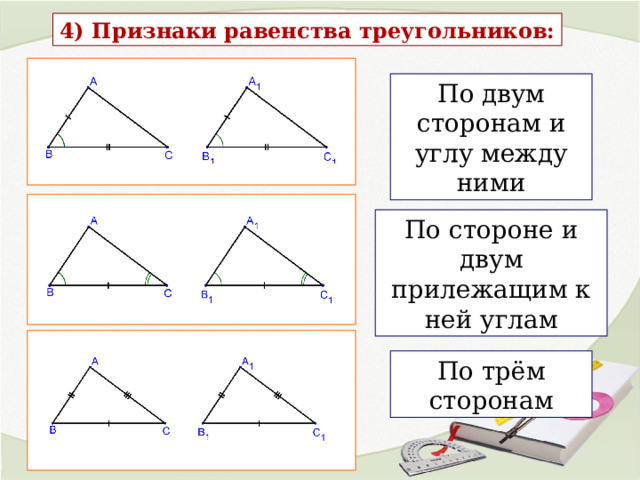
4) Признаки равенства треугольников:
По двум сторонам и углу между ними
По стороне и двум прилежащим к ней углам
По трём сторонам
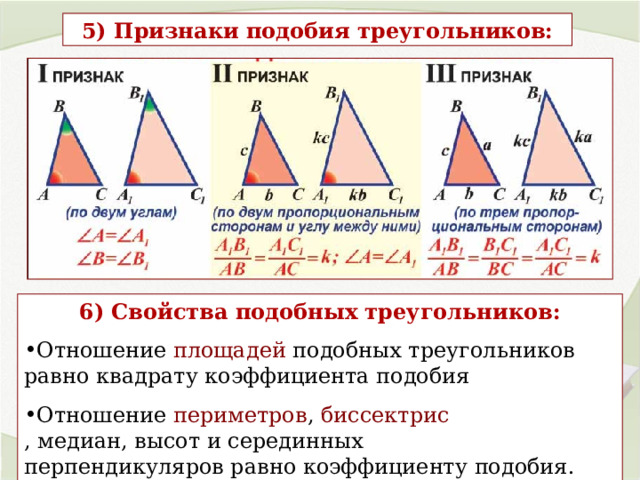
5) Признаки подобия треугольников:
6) Свойства подобных треугольников:
- Отношение площадей подобных треугольников равно квадрату коэффициента подобия
- Отношение периметров , биссектрис , медиан, высот и серединных перпендикуляров равно коэффициенту подобия.

7) Внешний угол треугольника — это угол, смежный с внутренним углом треугольника.
Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
∟ 1 = ∟А + ∟В
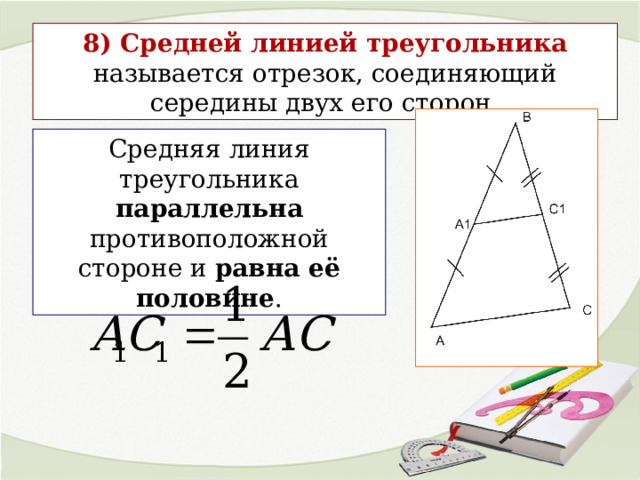
8) Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
Средняя линия треугольника параллельна противоположной стороне и равна её половине .
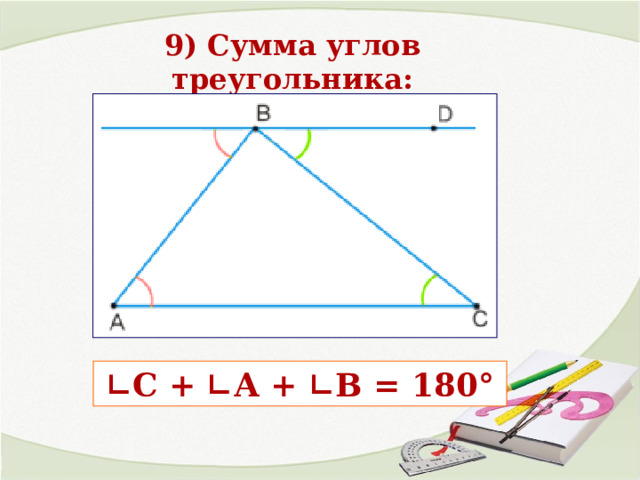
9) Сумма углов треугольника:
∟ С + ∟А + ∟В = 180 °
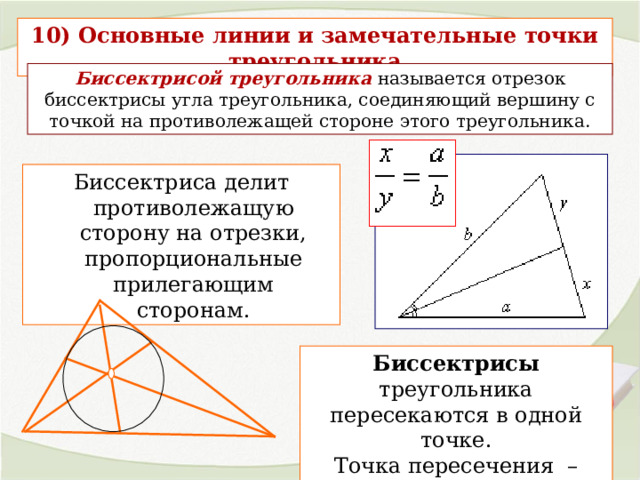
10) Основные линии и замечательные точки треугольника
Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противолежащей стороне этого треугольника.
Биссектриса делит противолежащую сторону на отрезки, пропорциональные прилегающим сторонам.
Биссектрисы треугольника пересекаются в одной точке.
Точка пересечения – центр вписанной окружности .

Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противолежащей стороны этого треугольника.
Свойства:
- Медиана разбивает треугольник на два треугольника одинаковой площади (равновеликие).
- Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины. Эта точка называется центром тяжести треугольника.
- Весь треугольник разделяется своими медианами на шесть равновеликих треугольников.
Медиана прямоугольного треугольника опущенная из вершины прямого угла равна половине гипотенузы .
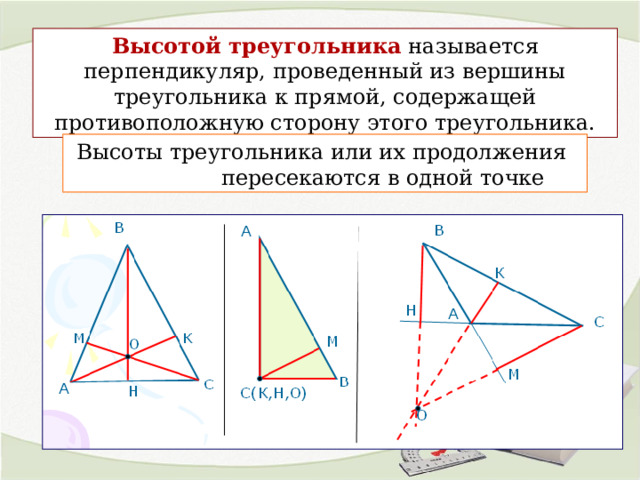
Высотой треугольника называется перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону этого треугольника.
Высоты треугольника или их продолжения
пересекаются в одной точке
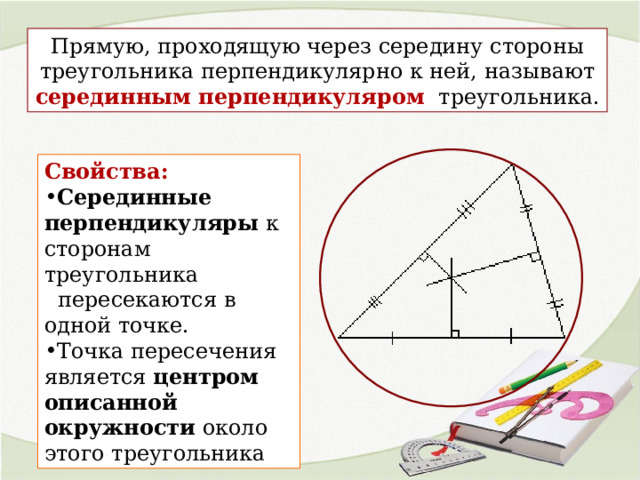
Прямую, проходящую через середину стороны треугольника перпендикулярно к ней, называют серединным перпендикуляром треугольника.
Свойства:
- Серединные перпендикуляры к сторонам треугольника
пересекаются в одной точке.
- Точка пересечения является центром описанной окружности около этого треугольника
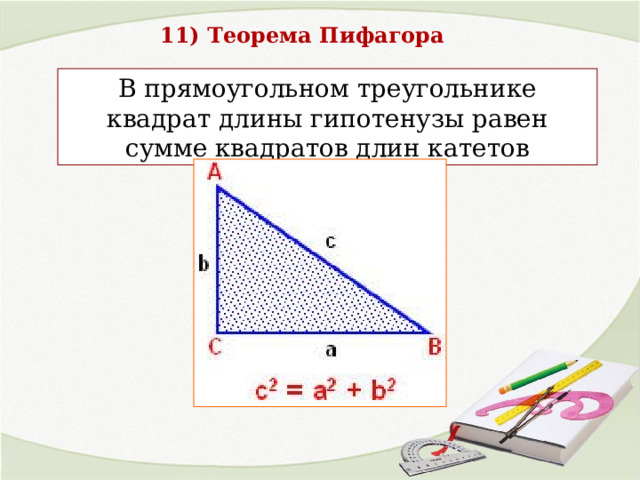
11) Теорема Пифагора
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов
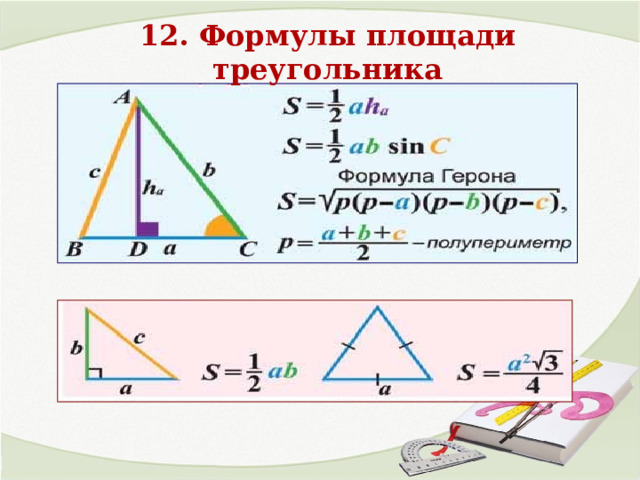
12. Формулы площади треугольника
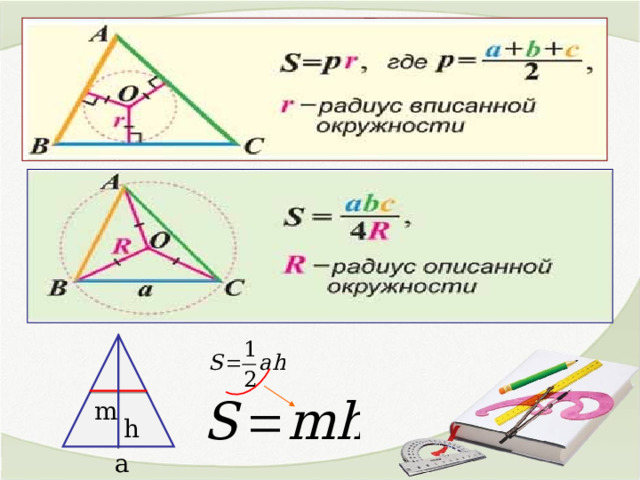
m
h
а
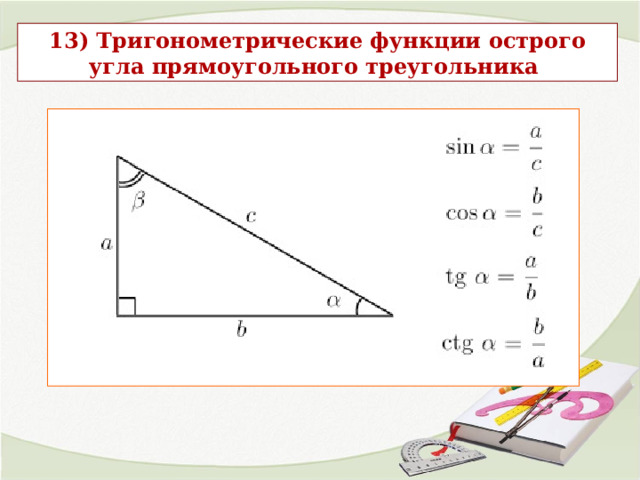
13) Тригонометрические функции острого угла прямоугольного треугольника
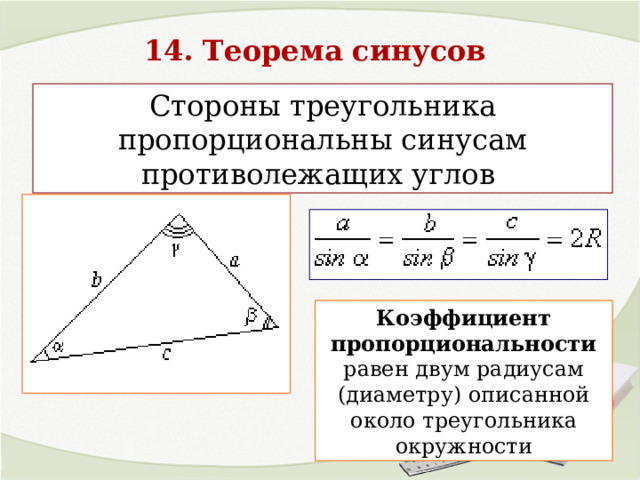
14. Теорема синусов
Стороны треугольника пропорциональны синусам противолежащих углов
Коэффициент пропорциональности равен двум радиусам (диаметру) описанной около треугольника окружности
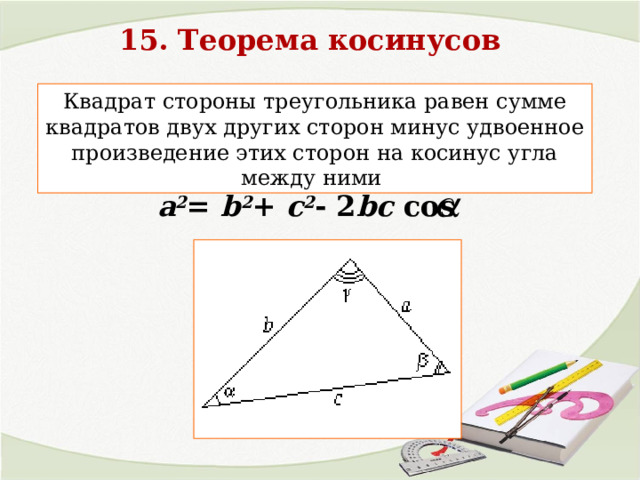
15. Теорема косинусов
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними
a 2 = b 2 + c 2 - 2 bc cos
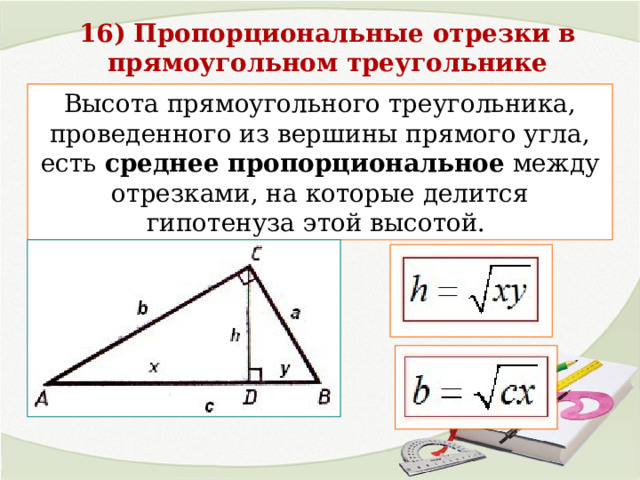
16) Пропорциональные отрезки в прямоугольном треугольнике
Высота прямоугольного треугольника, проведенного из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой.




































