Презентация к уроку по теме "Векторы в пространстве. Действия над векторами"

“ Математика - это наука о хитроумных операциях, производимых по специально разработанным правилам над специально придуманными понятиями“. Юджин Пол Вигнер американский физик

Век - тор

Шарада

Мой первый слог – почтенный срок,

Коль прожит он недаром.

Модель второго – на столе,

Румяна, с пылу, с жару.

Меня вы встретите везде –

Такой я вездесущий.

А имя громкое мое –

Латинское «несущий».

Векторы в пространстве. Действия с векторами

Задачи урока:

• рассмотреть понятие вектора в пространстве, его длины, понятие коллинеарных и равных векторов;
• определить действия над векторами в пространстве на основе сравнительного анализа темы «Векторы» 9 класса и темы «Векторы в пространстве»

Джоза́йя Уи́ллард Гиббс  ( англ.   Josiah Willard Gibbs ;  1839 — 1903 )  американский физик, физиохимик,математик,механик   один из создателей векторного анализа 

Понятие вектора появилось в 19 веке в работах математиков Г. Грассмана У. Гамильтона

Уильям Кингдон Клиффорд (1845–1879) английский математик

Современная символика для обозначения вектора r была введена в 1853 году французским математиком О. Коши .

Маргарита Иосифовна Алигер (1915-1992)

Родины себе не выбирают. 

Начиная видеть и дышать, 

Родину на свете получают 

Непреложно, как отца и мать.

  В 1942 году написала поэму «Зоя»,

посвящённую подвигу

Зои Космодемьянской

за которую получила

Сталинскую премию

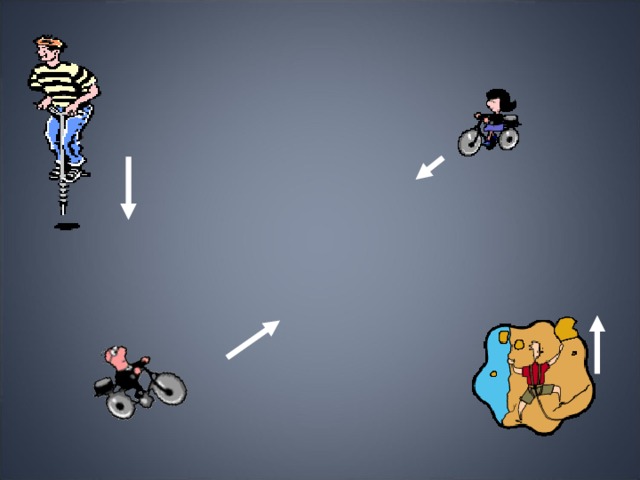
С какой скоростью и по каком курсу должен лететь самолет, чтобы за 2 ч пролететь точно на север путь, равный 300 км, если во время полета дует северо-западный ветер со скоростью 27 км/ч под углом 30 0 к меридиану?

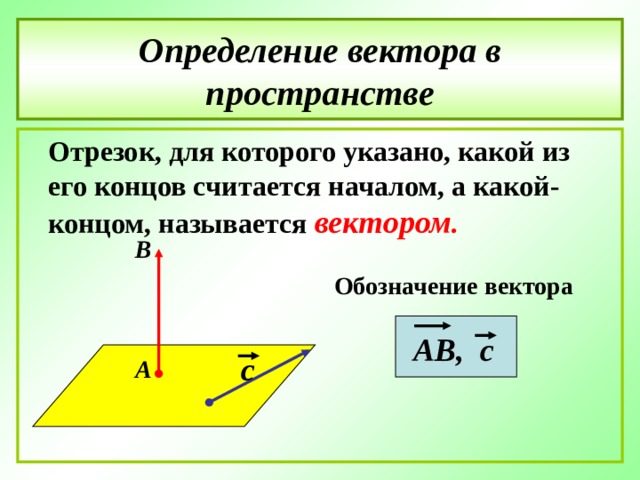
Определение вектора в пространстве

Отрезок, для которого указано, какой из его концов считается началом, а какой- концом, называется вектором .

В

Обозначение вектора

АВ, с

с

А

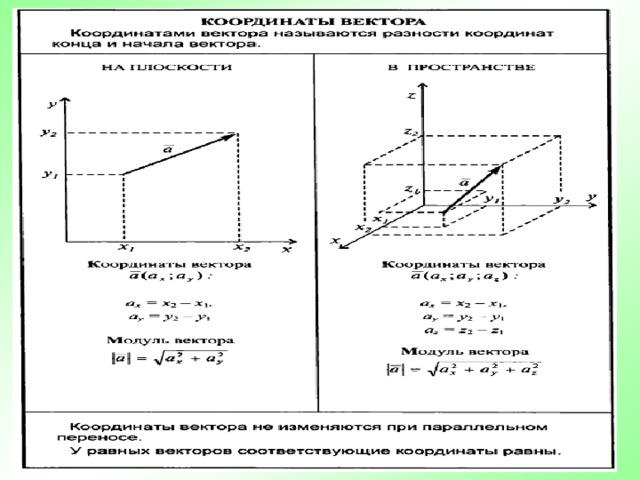
Координаты вектора.

А 1 (х 1 ; у 1 ; z 1 )

А 2 (x 2 ; y 2 ; z 2 )

A 1 А 2 (x 2 – x 1 ; y 2 – y 1 ; z 2 – z 1 )

Найдите координаты вектора МК, если М(10; -4; 2), К(16; 2; -5)

МК (16 – 10; 2 – (-4); -5 – 2)

Ответ: МК ( 6; 6; -7)

Длина вектора. (модуль, абсолютная величина)

a (x; y; z)

І a І = √ x² + y² + z²

Найдите модуль вектора а ( - 5; 1; 2)

ІаІ = √ 25 + 1 + 4 = √30

Ответ : √30

Любая точка пространства является нулевым вектором

Начало нулевого вектора совпадает с его концом

(Можно обозначать 0 или ММ)

Длина нулевого вектора равна 0

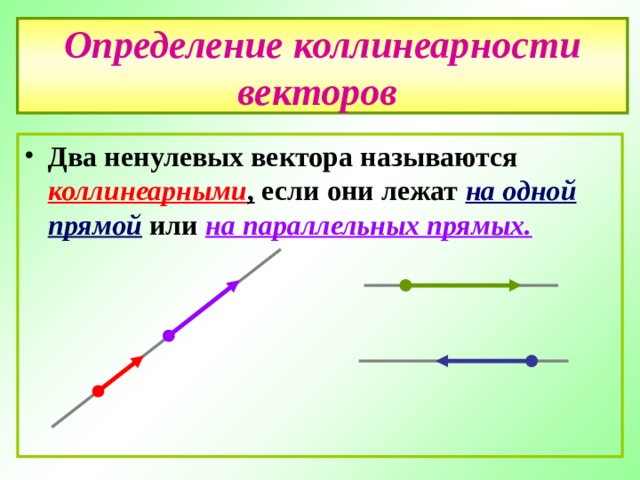
Определение коллинеарности векторов

• Два ненулевых вектора называются коллинеарными , если они лежат на одной прямой или на параллельных прямых.

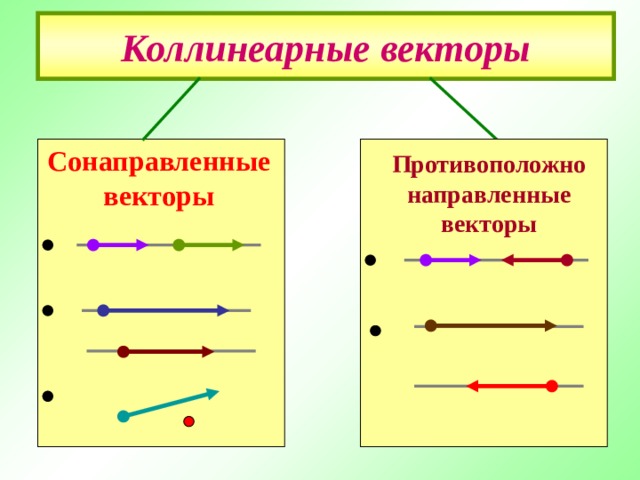
Коллинеарные векторы

Сонаправленные векторы

Противоположно направленные векторы

Признак коллинеарности векторов:

a (х 1 ; у 1 ; z 1 ) b(x 2 ; y 2 ; z 2 )

х 1 у 1 z 1

= =

x 2 y 2 z 2

При каких значениях m и n векторы а(4; -1; n ) и с(8; m ; 2 ) будут коллинеарны?

Составим пропорцию:

• -1 n

8 m 2

m = (-1 · 8) : 4 = -2; n = ( 4 · 2): 8 = 1;

Ответ: при m = -2 ; n = 1.

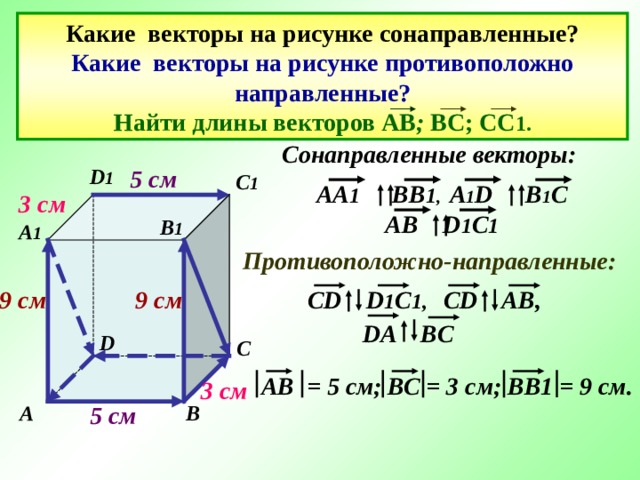
Какие векторы на рисунке сонаправленные? Какие векторы на рисунке противоположно направленные? Найти длины векторов АВ ; ВС; СС 1.

Сонаправленные векторы:

5 см

D 1

C 1

AA 1 BB 1 , A 1 D B 1 C

AB D 1 C 1

3 см

В 1

A 1

Противоположно-направленные:

CD D 1 C 1, CD AB,

DA BC

9 см

9 см

D

C

АВ = 5 см; ВС = 3 см; ВВ1 = 9 см.

3 см

A

B

5 см

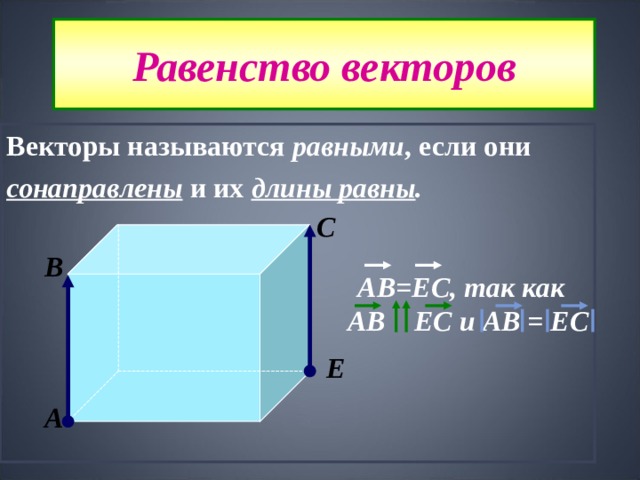
Равенство векторов

Векторы называются равными , если они

сонаправлены и их длины равны .

С

В

АВ=ЕС, так как

АВ ЕС и АВ = ЕС

Е

А

Противоположные векторы

Направления противоположны

Длины равны

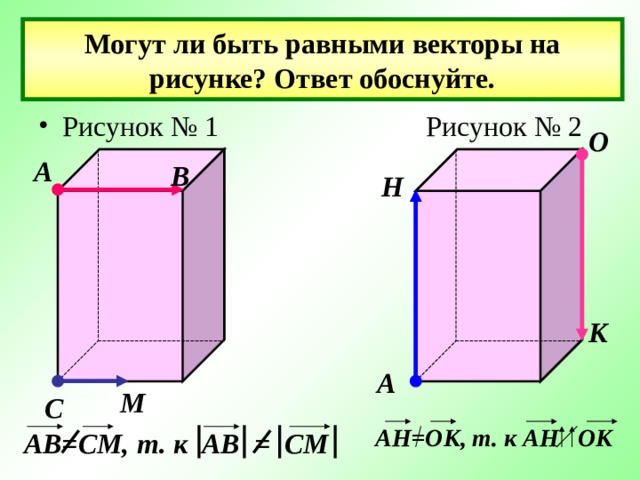
Могут ли быть равными векторы на рисунке? Ответ обоснуйте.

• Рисунок № 1 Рисунок № 2

О

А

В

Н

К

А

М

С

АН=ОК, т. к АН ОК

АВ=СМ, т. к АВ = СМ

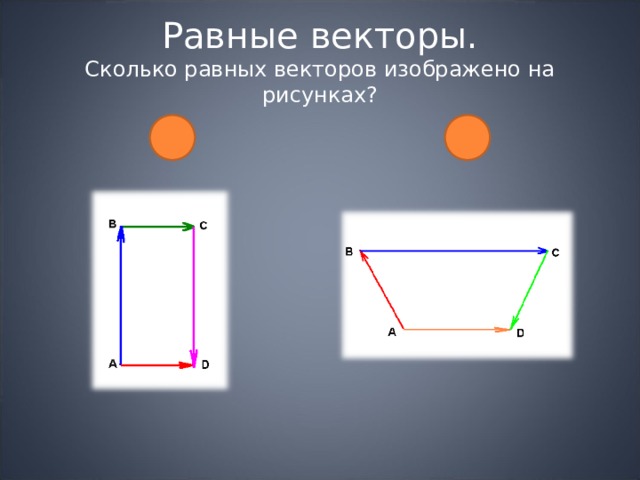
Равные векторы. Сколько равных векторов изображено на рисунках?

2

0

При каком значении n векторы а(4; 2 n - 1; -1) и в(4; 9 – 3 n ; -1) равны?

2n – 1 = 9 – 3n

2n + 3n = 9 + 1

5n = 10

n = 2

Ответ: при n = 2

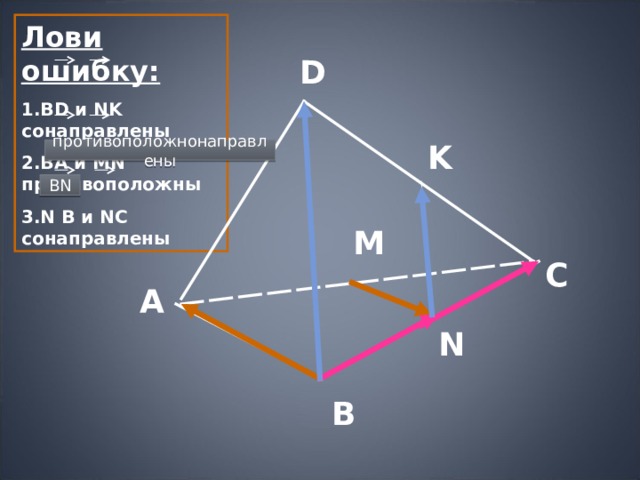
Лови ошибку:

• BD и NK сонаправлены
• ВА и MN противоположны
• N В и NC сонаправлены

D

K

противоположнонаправлены

В N

M

С

А

N

В

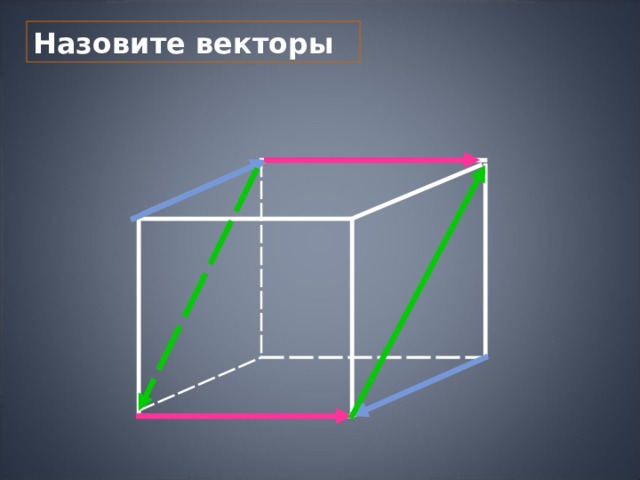
Назовите векторы

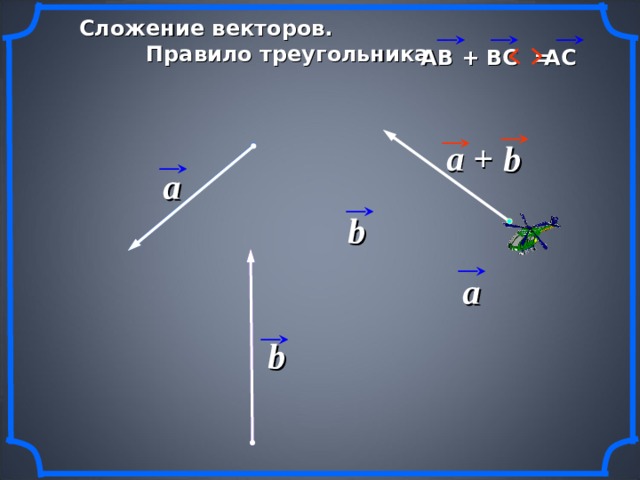
Сложение векторов.

Правило треугольника.

АВ + ВС =

АС

a +

b

a

b

a

b

31

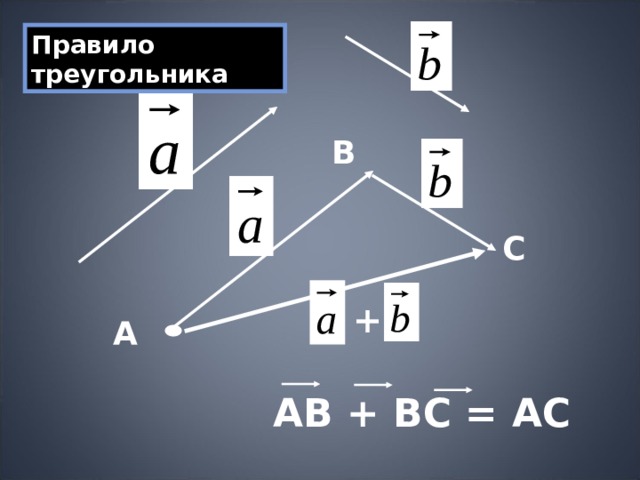
Правило треугольника

В

С

+

А

АВ + ВС = АС

+

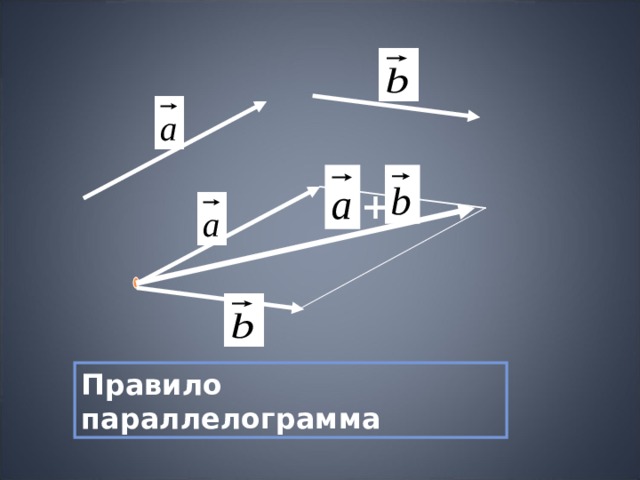
Правило параллелограмма

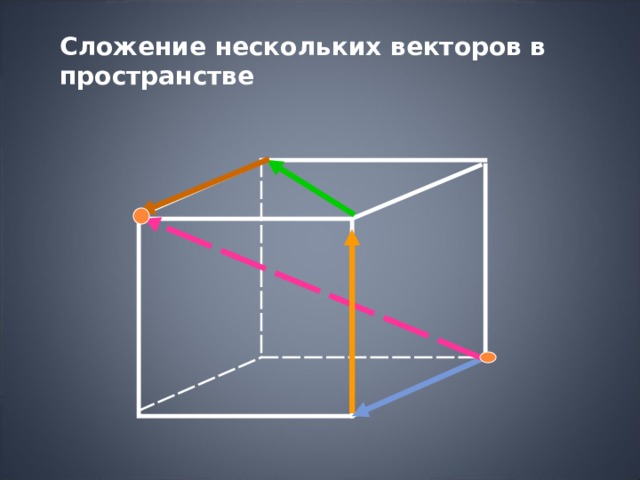
Сложение нескольких векторов в пространстве

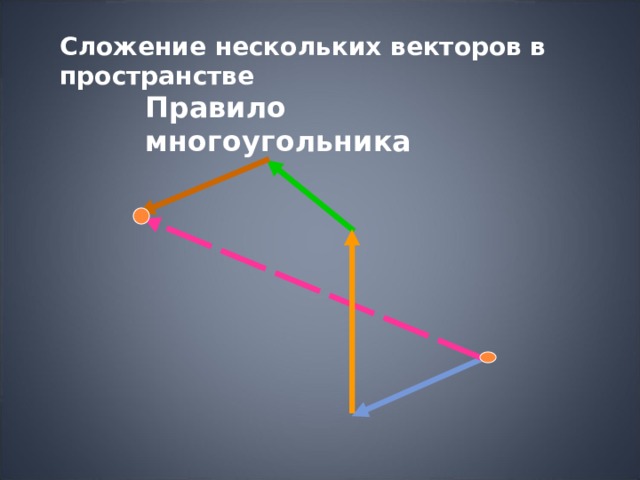
Сложение нескольких векторов в пространстве

Правило многоугольника

a+c+m+n

Сложение векторов.

Правило многоугольника.

П

О

В

Т

О

Р

И

М

АВ + ВС + С D + DO

= А O

n

m

a

m

n

c

c

a

36

Сумма векторов

Если a (х 1 ; у 1 ; z 1 ), а b (х 2 ; у 2 ; z 2 ),

то a + b = c , где

c (х 1 +х 2 ; у 1 +у 2 ; z 1 + z 2 )

5. Найдите сумму векторов а и b , если а(2; 3; -1), b (3; -2; 0)

Решение:

а + b = (2 + 3 ; 3 – 2; -1 + 0) = (5; 1; -1)

Ответ: (5; 1; -1)

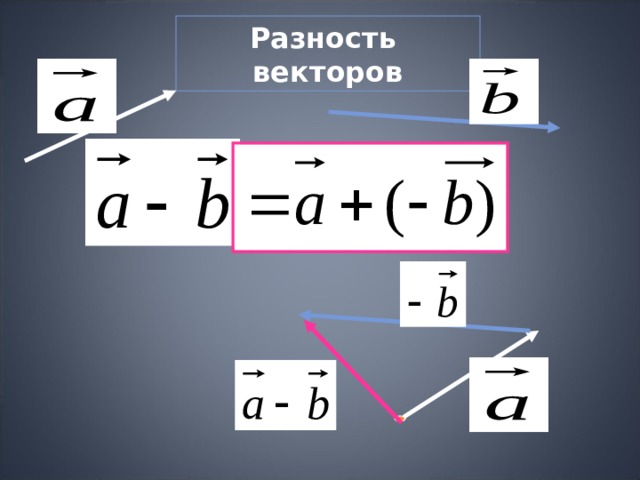
Разность векторов

Разность векторов

Если АВ(х 1 ; у 1 ; z 1 ), а АС(х 2 ; у 2 ; z 2 ),

то А В - А С = СВ, где

CB (х 1 - х 2 ; у 1 - у 2 ; z 1 - z 2 )

Найдите разность векторов а и b , если a (3; 7; 10), b (1; 9; -6 )

Решение:

a – b = (3 – 1; 7 – 9; 10 + 6) = (2; -2; 16)

Ответ: (2; -2; 16)

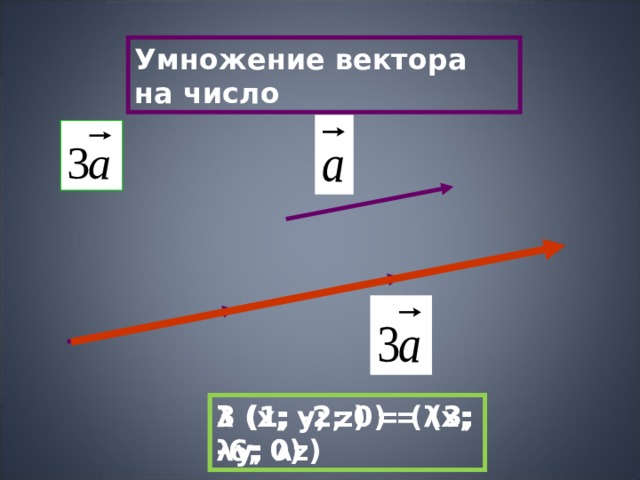
Умножение вектора на число

λ (x; y; z) = ( λ x; λ y; λ z)

3 (1; - 2 ; 0) = ( 3 ; - 6 ; 0)

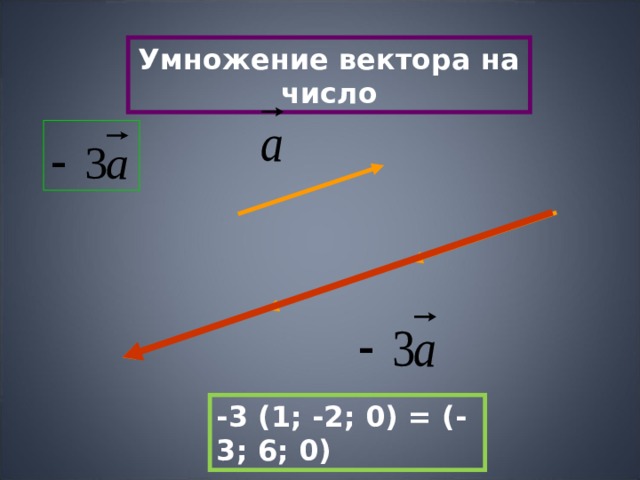
Умножение вектора на число

-3 (1; - 2 ; 0) = ( -3 ; 6 ; 0)

Умножение вектора на число

½ (1; - 2 ; 0) = ( ½ ; - 1 ; 0)

-½ (1; - 2 ; 0) = ( -½ ; 1 ; 0)

Найдите координаты вектора с = 2а -3 b , если а(7; -3; 0) и b (4; 1; -2)

Решение:

2а(14; -6; 0)

3 b (12; 3; -6)

2а - 3 b = (14 – 12; -6 -3; 0 – (-6)) = (2; -9; 6)

Найдите абсолютную величину вектора 3а, если а(4; -4; 2)

3а (12; -12; 6)

І3аІ = √144+ 144+ 36 =

= √324

І3аІ = 18

а (4; -4; 2)

ІаІ = √16+ 16+ 4 = √36 = 6

3 ІаІ = 3 ·6 = 18

1.Что называется вектором?

а)любой отрезок

б)отрезок, обозначенный двумя заглавными латинскими буквами

в) отрезок с выбранным направлением

2. Какой вектор является нулевым?

а)длина вектора равна 0

б)вектор лежит на прямой

в)вектор обозначен одной буквой

3. Векторы коллинеарны, если…

а)лежат на прямых

б)лежат на параллельных прямых

в)один из векторов нулевой

4. Векторы называются равными, если …

а)их длины равны

б)их модули равны и векторы направлены в одну сторону

в)они отложены от одной точки

• 5.Найдите сумму векторов: a ⃗(4;2;-4) и b ⃗(6;-4;10).
• (2; -6; 6); B) (2; -6;14); C) (10; -2; 6); D) (2; -2; 6); E) (10; -2; -14)
• 6.Умножьте вектор a ⃗(4;2;-1) на –3:
• А) (-12; -6; -3); B) (12; -6; -3); C) (-12; 6; 3); D) (-12; -6; 3); E) (-12; 6; -3).
• 7.Найдите разность векторов: a ⃗(6;-2;2) и b ⃗(4;-7;5).
• (-2; 5; -3); B) (2; -5; 3); C) (-2; -5; 3); D) (2; 5; 7); E) (2; 5; -3).
• 8.Найдите координаты вектора ( AB) ⃗, если A(2;-5;3) и B(5;1; -2).
• (3; -6; 5); B) (3; 6;-5); C) (-3; 6; -5); D) (7; -4; 1); E) (-3; 6; 5).
• 9.Найдите длину вектора ( AB) ⃗, если A(-1;-1;1) и B(-3;1; 0).
• 4; B) 9; C) 5; D) 3; E) √3.

Домашнее задание Выучить определения: Вектор Коллинеарные векторы Сонаправленные и противоположно направленные векторы Равные векторы Сумма и разность векторов Умножение вектора на число Задача. Найти значения m и n , при которых векторы а(3; m ; 6) и b (-6; 4; n ) коллинеарны