Презентация к уроку: "Понятие первообразной"

Тема урока

«Понятие первообразной»

учитель математики

высшей категории

Серевко И. Д.

Цели урока:

• - Сформировать представление о понятии "первообразная", способствовать формированию умений применять полученные знания в новой ситуации. Установить связь между производной и первообразной, формировать умение проверять является ли данная функция первообразной для другой, заданной на некотором числовом промежутке функции.
• - развивать навыки мыслительной деятельности при анализе и структурировании учебного материала
• - Способствовать привитию культуры умственного труда, воспитывать организованность и сосредоточенность

1

• Организационный этап.
• Организационный этап.

2

• Постановка цели и задач урока. Мотивация учебной деятельности учащихся.
• Постановка цели и задач урока. Мотивация учебной деятельности учащихся.

3

• Актуализация знаний через обсуждение заданий на установление связи между производной и первообразной.
• Актуализация знаний через обсуждение заданий на установление связи между производной и первообразной.

4

• Введение определение первообразной.
• Введение определение первообразной.

5

• Формирование умения проверять, является ли данная функция первообразной для другой, заданной на некотором промежутке функции или не является.
• Формирование умения проверять, является ли данная функция первообразной для другой, заданной на некотором промежутке функции или не является.

6

• Усвоение определения первообразной через выполнение примеров .
• Усвоение определения первообразной через выполнение примеров .

7

• Постановка домашнего задания, инструктаж о его выполнении.
• Постановка домашнего задания, инструктаж о его выполнении.

8

• Подведение итогов через постановку вопросов, рассматриваемых на этапах урока. Рефлексия.
• Подведение итогов через постановку вопросов, рассматриваемых на этапах урока. Рефлексия.

ПЛАН УРОКА

Найти производную функций

а) ( )'

б) ( )'

в) ( )'

г) ( )'

д) ( )'

е) ( )'

Найти производную функций

Взаимно-обратные операции в математике

Обратная

Прямая

Сложение

x 2

Возведение в квадрат

sin α = a

Синус угла

arcsin a = α a ∈ [-1;1]

Арксинус числа

Умножение

(x n )' = nx n-1

Дифференцирование

Деление

∫ nx n-1 dx = x n + C

Интегрирование

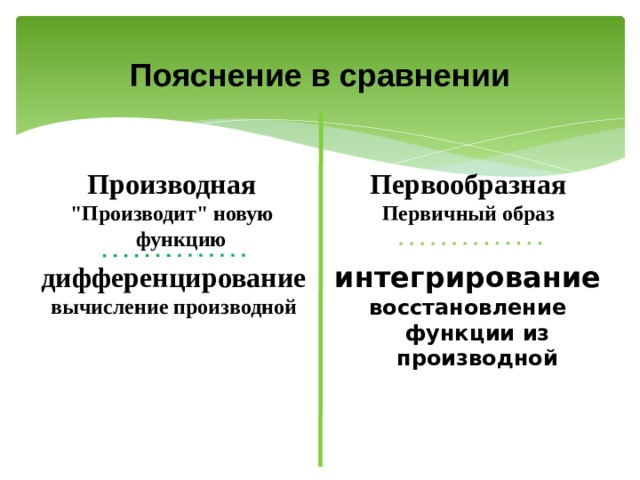
Пояснение в сравнении

Производная

Первообразная

"Производит" новую функцию

Первичный образ

дифференцирование

вычисление производной

интегрирование

восстановление функции из производной

Определение первообразной

y = F(x) называют первообразной для y = f(x) на промежутке X, если при x ∈ X

F'(x) = f(x)

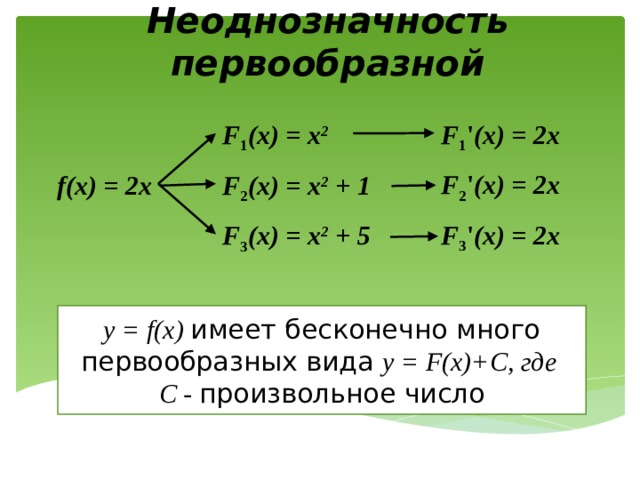
Неоднозначность первообразной

F 1 ' (x) = 2x

F 1 (x) = x 2

F 2 ' (x) = 2x

f(x) = 2x

F 2 (x) = x 2 + 1

F 3 ' (x) = 2x

F 3 (x) = x 2 + 5

y = f(x) имеет бесконечно много первообразных вида y = F(x)+C, где

C - произвольное число

f(x)

F(x)

1

k

kx+C

Правила интегрирования

Задача №6.2 (г) стр. 170 уч. С. М. Никольского.

№ 6.8.в) стр.171 уч. С. М. Никольского

f(x=

F(x) = +с

1.Первообразная для функции f(x)  =х+ является функция F(x):

А) F(x)= - +с В) F(x)=+c

Б) F(x)= ++с Г) F(x)= 2- cos x + c

2. Данная функция F(x)= -3 +7 является первообразной для функции f(x) :

С) f(x)  =4-2х О) f(x)  =-3х +7

Р) f(x)  =4-6х

3. Данная функция F(x)= является первообразной для функции f(x) :

А) f(x)= - В) f(x)= - +1

Б) f(x)= 2 +1 Г) f(x)= -

4. Ошибка при нахождении первообразной для функции f(x) = находится под буквой:

А) F(x)= tgх +4

Б) F(x)= tgх – 5 В) F(x)= - tgх +4

5 . Какова функция интегрирования?:

О) вычисление первообразной

С) вычисление производной

Домашнее задание

6.П.6.1Первообразная. Памятка.

1 уровень: №6.2(д), №6.7(б)

2 уровень: №6.5(а), №6.8.(б).

Подведение итогов

Рефлексия

Все понял (а), все успел(а)

Частично не понял(а), не все успел(а)

Спасибо

за урок!