Презентация к уроку "Виды функций. Непрерывность функций."

Раздел 7. Функции и графики

Виды функций. Непрерывность функций.

Что такое функция?

Какие функции вы знаете?

СТЕПЕННЫЕ ФУНКЦИИ

История функций

• Идея функциональной зависимости восходит к древности .
• Ее содержание обнаруживается уже в первых математически выраженных соотношениях между величинами, в первых правилах действий над числами

Квадратура круга

• Так, вавилонские ученые (4-5 тыс.лет назад) пусть несознательно, установили, что площадь круга является функцией от его радиуса посредством нахождения грубо приближенной формулы: S=3r².

• Примерами табличного задания функции могут служить астрономические таблицы вавилонян, древних греков и индийцев,

Античные определения конических сечений

• Эти кривые выступали в качестве геометрических образов соответствующей зависимости.

• Начиная лишь с 17 века, в связи с проникновением в математику идеи переменных, понятие функции явно и вполне сознательно применяется

• Франсуа Виет и Рене Декарт разработали единую буквенную математическую символику, которая вскоре получила всеобщее признание.

• Введено было единое обозначение: неизвестных - последними буквами латинского алфавита - x, y, z, известных - начальными буквами того же алфавита - a, b, c, ... и т.д.

• В 1671 году Ньютон под функцией стал понимать переменную величину, которая изменяется с течением времени (называл в « флюентой »).

• Само слово «функция» (от латинского functio -совершение, выполнение) впервые было употреблено немецким математиком Лейбницем в 1673г. в письме к Гюйгенсу (под функцией он понимал отрезок, длина которого меняется по какому-нибудь определенному закону), в печати ввел с 1694 года

Степенная функция

• Это функция вида y =х n , где n  - заданное число, называемое показателем степени

Степенная функция

y =х n

Степенные функции общего вида

• f (х)= 2х 3 -9х 2 -24х
• f (х)= 6х 4 -3х 2
• f (х)= 3х 5 +5х 3 -5

Графики типичных степенных функций с целым положительным

• кубическая парабола

• Аналитическое задание этой функции
• у=х ³
• Табличное задание

х

у

-2

-1

-8

0

-1

1

0

1

2

8

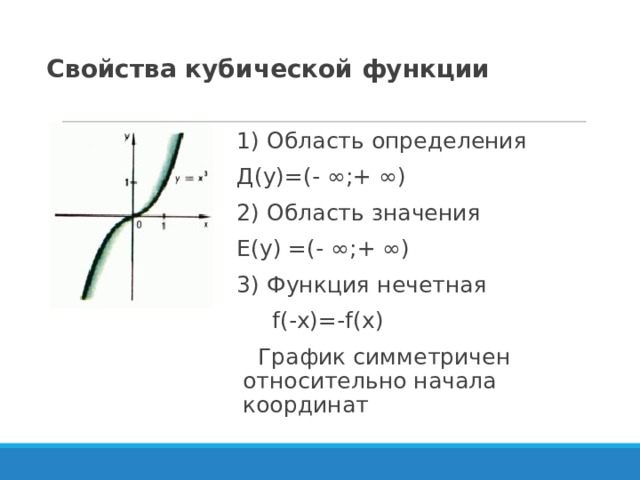
Свойства кубической функции

1) Область определения

Д(у)=(- ∞;+ ∞)

2) Область значения

Е(у) =(- ∞;+ ∞)

3) Функция нечетная

f(-x)=-f(x)

График симметричен относительно начала координат

Свойства

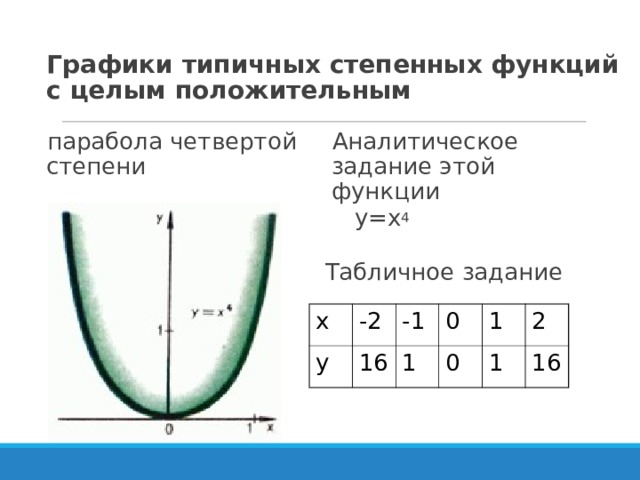
Графики типичных степенных функций с целым положительным

• парабола четвертой степени

• Аналитическое задание этой функции

у=х 4

Табличное задание

х

у

-2

-1

16

0

1

0

1

1

2

16

Свойства

• При   n=1 степенная функция  является линейной функцией (график прямая), при   n=2 квадратичной функцией (график парабола)

Степенные функции вокруг нас

• Объем куба V  есть степенная функция от x  (длины его ребра):

V= х 3

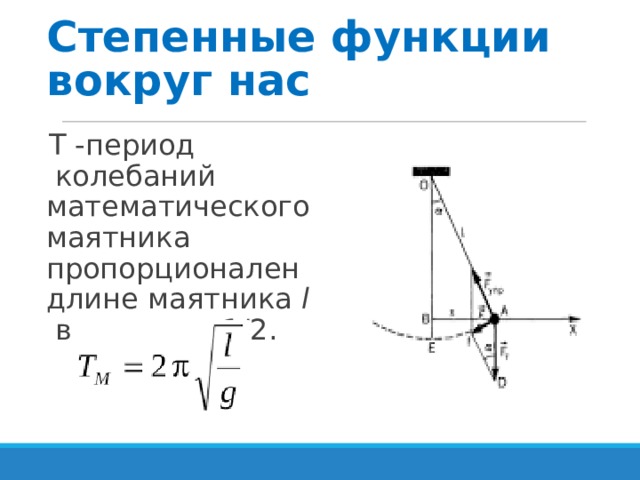
Степенные функции вокруг нас

• T -период  колебаний математического маятника пропорционален длине маятника l  в степени 1/2 .

Степенные функции вокруг нас

• Если газ расширяется или сжимается без теплообмена с окружающей средой, то его давление P  и объем V  связаны формулой VP k   =C (для воздуха, например, k=-1 ,4 )

Траекторией движения при бросании тела вверх будет парабола.

ОПЫТ АРХИМЕДА

• По легенде, Архимед с помощью системы зеркал в виде параболлоида поджег вражеские корабли римской эскадры.

• По дошедшей до нас легенде Архимед построил вогнутые зеркала и с их помощью сжег римские корабли.
• Большинство ученых отвергают эту легенду, поскольку такие зеркала должны были бы иметь слишком большие размеры, а это невозможно при тогдашнем уровне техники

• Любая прямая, параллельная оси симметрии параболы, после отражения от параболы проходит через ее фокус

На основании этого вывода сейчас существует множество изобретений

• Солнечная зажигалка

• Солнечные батареи и печи

«Солнечный меч» — орбитальное космическое оружие Третьего Рейха

• Самым амбициозным невоплощенным проектом остался циклопический Sonnengewehr – «Солнечная пушка» – орбитальное оружие, идеальное «оружие возмездия», о котором грезил в последние свои годы Гитлер .

• Функция-  зависимость переменной  у   от переменной  x,   если каждому значению  х  соответствует единственное значение  у . Переменная х-  независимая переменная или аргумент. Переменная у-  зависимая переменная Значение функции-  значение  у , соответствующее заданному значению  х .

СПОСОБЫ ЗАДАНИЯ ФУНКЦИИ.

Табличный способ

• Задании таблицы отдельных значений аргумента и соответствующих им значений функции.

• При табличном способе задания функции можно приближенно вычислить не содержащиеся в таблице значения функции, соответствующие промежуточным значениям аргумента.
• Для этого используют способ интерполяции .

Графический способ

• Графиком функции  y = f(x)  называется множество всех точек плоскости, координаты которых удовлетворяют данному уравнению.

Графический способ задания функции не всегда дает возможность точно определить численные значения аргумента.

Однако он имеет большое преимущество перед другими способами - наглядность.

Аналитический способ.  

Функция может быть определена разными формулами на разных участках области своего задания.

• Закон, устанавливающий связь между аргументом и функцией, задается посредством формул.
• Этот способ дает возможность по каждому численному значению аргумента  x  найти соответствующее ему численное значение функции  y  точно или с некоторой точностью .

Словесный способ

• Этот способ состоит в том, что функциональная зависимость выражается словами.
• Пример:  

функция  E(x)  —  целая часть числа  x .

Что общего у параболы и квадрата?

Определите, какие из перечисленных точек принадлежат графику функции у(х)= - 2х+4.

• А(0;4); В(5;7); С(2;0); Д(-1;10)

Элементарные функции

• Степенная.
• Показательная
• Логарифмическая
• Тригонометрические

Схема исследования функции

• 1 . Область определения
• 2. Область значения
• 3. Четность
• 4. Периодичность
• 5. Промежутки возрастания и убывания
• 6. Экстремумы
• 7. Точки пересечения с осями координат
• 8. Промежутки знакопостоянства
• 9. График функции.

• Вычислите значение выражения 1/(х-3) при х=3
• На ноль делить нельзя!
• А что будет происходить с функцией при х=3?
• Проверим

Предел

• Функция  f(x)  имеет предел  A  в точке  x0  если для всех значений  x , достаточно близких к  x0 , значение  f(x)  близко к  A .

Предельный переход

Непрерывность

• Функция  f  ( x ), определенная в некоторой окрестности точки  a , называется непрерывной в этой точке, если предел функции в этой точке равен значению функции в этой точке

Точки разрыва

• Точка  a  называется  точкой разрыва , если эта функция либо не определена в точке  a , либо определена, но не является непрерывной в точке  a .

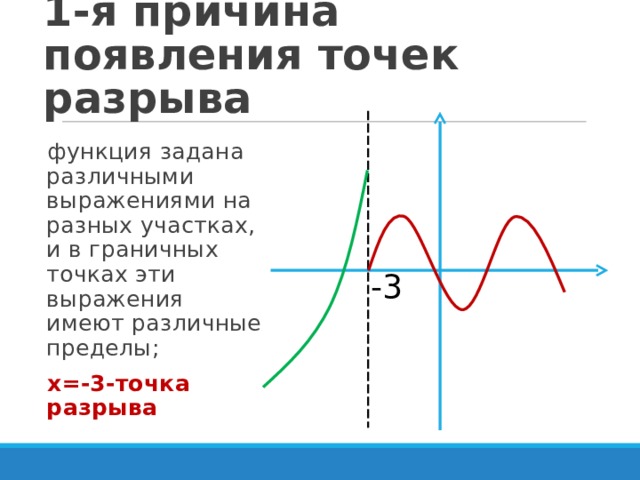
1-я причина появления точек разрыва

• функция задана различными выражениями на разных участках, и в граничных точках эти выражения имеют различные пределы;
• х=-3-точка разрыва

-3

2-я причина появления точек разрыва

• функция не определена в данной точке.
• х=1-точка разрыва

• Область определения функции-  все значения, которые принимает независимая переменная Д(у) Область значений функции (множество значений)-  все значения, которые принимает функция.Е(у)

Вычислите пределы и найдите области определения соответствующих функций

• 1) lim(2x-8)
• 2) lim((x²-1)/x³)
• 3) lim(x/(9-x))
• 4) lim(2x³/x⁶)
• 5) lim(sinx)

x→1

x→0

x→9

x→∞

x→o

Вопрос №1 Аргумент это:

• А) х
• В) у
• С) f(x)

Вопрос №2 Аналитический способ задания функции это:

• А) график
• В) формула
• С) таблица

Вопрос №3 Какой способ задания функции здесь лишний:

• А) графический
• В) словесный
• С) художественный

Вопрос №4 Предел равен:

• А) нулю
• В) бесконечности
• С) единице

Вопрос №5 Какой х не входит в область определения функции у=1/(х-2) :

• А) 0
• В) -2
• С) 2

Домашнее задание

• 1) Знать конспект
• 2) Определите, какие из перечисленных точек принадлежат графику функции у(х) = 2х-3.
• А(4;5); В(-3;5); С(0;-3); Д(5;- 3).
• 3) Найдите области определения функций
• у=3/(х-9)
• у=√2х+14
• У=5х-1