Презентация Лист Мебиуса

Муниципальное бюджетное образовательное учреждение Краснинская средняя общеобразовательная школа

Лист Мёбиуса

Работу выполнила: Сысина Анна,

2б класс

Руководитель: Серова Надежда Николаевна

Красный 2015

Цели: изучить свойства листа Мёбиуса, рассмотреть его применение на практике.

Задачи исследования:

• выявить источники и литературу по данной теме и проанализировать их;
• познакомиться с историей возникновения листа Мёбиуса;
• научиться и научить других, изготавливать лист Мёбиуса;
• изучить разнообразные свойства листа Мёбиуса;
• выяснить, где применяется лист и его свойства;
• изучить опыты с листом Мёбиуса, которые описываются в математической литературе, и провести эксперименты;
• обобщить полученную информацию.

Объект нашего исследования – лента Мёбиуса

Методы исследования:

• анализ математической литературы,
• изучение, исследование и сбор информации,
• практический эксперимент.

Гипотеза: Лист (лента) Мёбиуса таит в себе много загадок.

Лист Мёбиуса – символ математики, Что служит высшей мудрости венцом… Он полон неосознанной романтики: В нем бесконечность свернута кольцом.

В нем – простота, и вместе с нею – сложность, Что недоступна даже мудрецам: Здесь на глазах преобразилась плоскость В поверхность без начала и конца.

Здесь нет пределов, нет ограничений, Стремись вперед и открывай миры, Почувствуй силу новых ощущений, Прими познанья высшего дары…

Иванова Н. Ю.

Многие знают, что такое лента (лист) Мёбиуса.

Тем, кто ещё не знаком с удивительным листом, который относится к «математическим неожиданностям», я предлагаю провести исследование и окунуться в светлое чувство познания.

Август Фердинанд Мёбиус (1790-1868)

Величайший геометр XIX в.,

ученик «короля математиков» К. Гаусса.

Первоначально был астрономом.

В возрасте 68 лет сделал открытие односторонних поверхностей, одна из которых – лист (лента) Мёбиуса.

История открытия

Лист Мёбиуса - символ современной математики.

Открытию «листа» способствовала служанка, неправильно сшившая концы ленты.

Момент создания «ленты» стал началом рождения новой науки – ТОПОЛОГИИ.

Топология изучает такие свойства фигур, которые

не меняются при любых

деформациях,

производимых без

разрывов и склеиваний.

План создания «ленты»:

• Взять бумажную полоску шириной 3 см.
• Склеить ее так, чтоб точка A совпала с точкой D, а точка B – с точкой C (т.е. склеить её концы, предварительно повернув один из них на 180 градусов).

А

С

3 см

В

D

Получила такое перекрученное кольцо - «лист» Мёбиуса.

Сколько сторон у листа Мёбиуса?

Задалась вопросом:

У него ОДНА сторона.

Что будет, если разрезать обычный лист бумаги?

А что случится, если разрезать вдоль посередине это кольцо Мёбиуса по всей длине?

Опыт 1. Несколько перекручиваний

Я сначала склеила полоску без перекручивания, и разрезала простое кольцо ножницами вдоль.

Получилось два кольца.

Затем взяла лист Мёбиуса (кольцо, перекрученное на пол-оборота) и его разрезала вдоль, получила одно кольцо в виде восьмёрки Лента перекручена два раза

Продолжала перекручивать полоски бумаги перед склеиванием, каждый раз увеличивая число полуоборотов на один.

Число полуоборотов 3

Число полуоборотов 4

Число полуоборотов 5

Результаты записала в таблицу 1

Вывод:

• Если сделать нечётное количество полуоборотов и разрезать вдоль, то получится одно кольцо, длиннее прежнего и завязанное узлом.
• Если сделать чётное количество полуоборотов и разрезать вдоль, то всегда получится 2 кольца прежней длины, причём они будут соединены, и сложность соединения будет возрастать с ростом количества полуоборотов.

Опыт 2. Несколько разрезаний

Для этого исследования я использовала более широкие полосы – примерно 5 см. Склеила три листа Мёбиуса и разрезала одно кольцо вдоль, отступив от края на1/3

Получила два кольца: одно – лист Мёбиуса первоначальной длины, второе кольцо в виде восьмёрки в два раза длиннее, ширина каждого втрое уже первоначального. Оба кольца соединены друг с другом.

Далее разрезала другое кольцо вдоль, отступив от края на 1/4,

При разрезании листа Мёбиуса вдоль его границы, отступая от края на1/5 его ширины

Лист Мёбиуса той же длины, что и первоначальное , две восьмёрки в два раза длиннее

Результаты этого исследования поместила в таблицу 2

Вывод:

При разрезании листа Мёбиуса вдоль его границы, отступая от края на 1/3, на 1/4 его ширины, всегда получается два кольца. Одно – лист Мёбиуса первоначальной длины, второе кольцо в виде восьмёрки всегда в два раза длиннее и в несколько раз уже ( не считая первого раза). Кольца всегда соединены. Если на 1/5 его ширины, то получается 3 кольца. Одно-лист Мёбиуса и две восьмёрки. Кольца соединены.

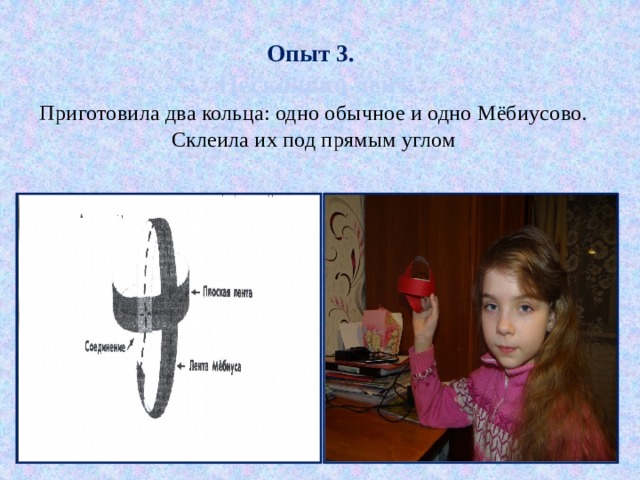
Опыт 3. Несколько лент Приготовила два кольца: одно обычное и одно Мёбиусово. Склеила их под прямым углом

Затем оба разрезала вдоль и получила квадрат

Вывод:

Лист Мёбиуса – удивительный феномен. Его можно исследовать до бесконечности, мы рассмотрели лишь некоторые его свойства :

• имеет одну поверхность (односторонний);
• при склеивании его с разным количеством полуоборотов получается также односторонняя поверхность;
• при разрезании листа Мёбиуса с различным количеством полуоборотов получается либо одно кольцо, либо два;
• при разрезании двух склеенных перпендикулярно лент между собой получается квадрат либо без узла, либо с узлом.

Применение

Лист Мёбиуса используется в кинозаписи, в звукозаписи. С ним проводят опыты и трюки фокусники в цирке. Его применяют при выполнении различных технических работ. Если бы лента Мёбиуса была сделана из очень эластичной резины, то её край можно было бы деформировать в окружность, а тогда сама лента превратилась бы в торбу, которая пригодна для ношения вещей, хотя у неё нет ни внутренней, ни внешней стороны.

Полоса ленточного конвейера, выполненная в виде листа Мёбиуса, позволяет ему работать дольше в два раза

Наша Вселенная вполне вероятно замкнута в ленту Мёбиуса

Физики утверждают, что отражение в зеркале основано на свойствах ленты Мёбиуса

Лист Мёбиуса в природе

В матричном принтере красящая лента имеет вид листа Мёбиуса

Лист Мёбиуса в одежде

«Лист» Мебиуса в искусстве

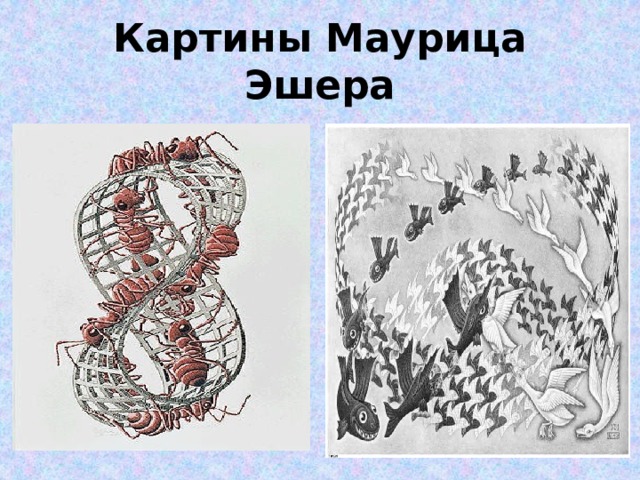
Картины Маурица Эшера

Картины Маурица Эшера

Памятники

В России г. Москва

В Белоруссии

Памятники

В Германии

В Латвии

г. Франкфурт

В Казахстане существует задумка построить библиотеку в форме ленты Мёбиуса .

Используемая литература:

• Фукс Д.  Лента Мёбиуса. Вариации на старую тему  // «Квант», № 1, 1979.
• Сайт учителя математики.[Электронный ресурс] – Режим доступа: http://le-savchen.ucoz.ru/publ/1-1-0-31 свободный
• Секреты ленты МЁБИУСА. Катушка МЁБИУСА. [Электронный   ресурс]  –  Режим   доступа: http://bornovec.ru/fizika/index.htm свободный

Спасибо за внимание!