Презентация "Моя педагогическая философия"

Моя педагогическая философия

Алексеева Наталья Федоровна,

учитель математики Мухоршибирской СОШ №1

« Школьная математика – это содержательное, увлекательное и доступное поле деятельности, дающее ученику богатую пищу для ума, связывающее его с общечеловеческой культурой, формирующее важнейшие черты личности» / Башмаков М. /

Я - учитель математики

Я – член педагогического моего коллектива

Я – выпускница моей школы

Наши школьные учебники математики изобилуют математическими фактами в виде аксиом, определений, теорем, формул и других объектов.

Часто не дается никаких объяснений, откуда что произошло и зачем это нужно знать.

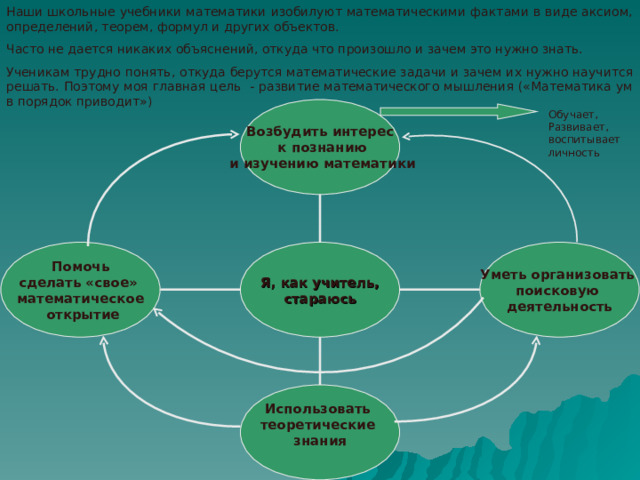
Ученикам трудно понять, откуда берутся математические задачи и зачем их нужно научится решать. Поэтому моя главная цель - развитие математического мышления («Математика ум в порядок приводит»)

Возбудить интерес

к познанию

и изучению математики

Обучает, Развивает, воспитывает личность

Я, как учитель,

стараюсь

Уметь организовать

поисковую

деятельность

Помочь

сделать «свое»

математическое

открытие

Использовать

теоретические

знания

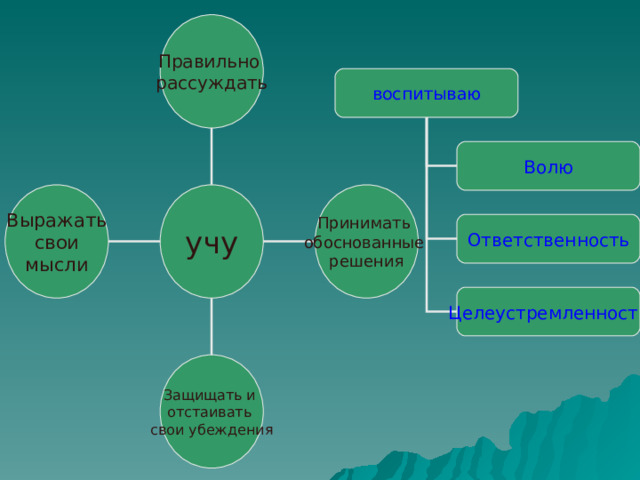
Правильно

рассуждать

воспитываю

Волю

Выражать

свои

мысли

учу

Ответственность

Целеустремленность

Защищать и

отстаивать

свои убеждения

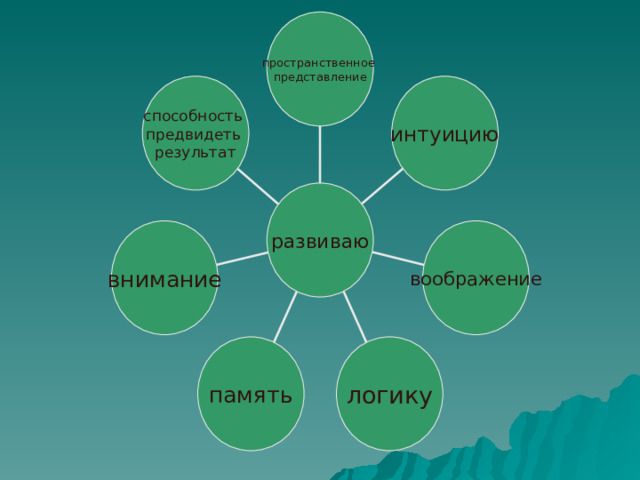
пространственное

представление

способность

предвидеть

результат

интуицию

развиваю

внимание

воображение

память

логику

Основная форма деятельности, развития математического мышления – урок.

«Подготовка к уроку - это подготовка к руководству мышлением

учащихся, а мышление всегда начинается с вопросов».

В.А. Сухомлинский

Урок начинается не со звонка, а за долго до него.

Задачи урока математики

1. Научить анализу полученной информации

2. Помочь в овладении математическим языком и математической символикой

3. Помочь учащимся овладеть эвристическими методами работы над задачей

4. Организовать поисковую деятельность

5. Создать ситуацию успеха.

«Чем теснее связан данный урок с другими уроками по данному разделу программы, тем законченное, цельнее урок сам по себе, тем глубже будут знания учащихся»

В. А.Сухомлинский

• Продумывание плана сразу нескольких уроков.
• Формулировка триединой цели каждого урока и его места в системе уроков.
• Определение роли учителя и ученика на каждом уроке
• Составление плана изучения отдельных тем и разделов. Это дает возможность устанавливать взаимосвязь между уроками и довиваться рационального использования времени.
• На основе этого составляются поурочные планы.

СОЗДАНИЕ ПСИХОЛОГО-ПЕДАГОГИЧЕСКИХ УСЛОВИЙ ДЛЯ РАЗВИТИЯ УЧЕБНОЙ МОТИВАЦИИ УЧАЩИХСЯ ПРИ ИЗУЧЕНИИ МАТЕМАТИКИ

Обучение математике - это в первую очередь решение задач. Поэтому задачи выступают как главное средство мотивации учащихся. Умение решать задачи - критерий успешности обучения математике.

• Новизна содержания:

Получение или показ через задачу новых для учащихся математических сведений

Важно новые знания не предлагать учащимся в готовом виде, а создавать такие проблемные ситуации, при которых ученик ставится в положение исследователя, заинтересованного в решении проблемы, и стремится самостоятельно найти решение, сделать «открытие».

2. Отражение связи с практикой

Если учащийся видит в решаемой задаче возможность применить полученные знания на практике ( в повседневной жизни, при изучении других предметов и т.д.), то появляется и интерес к её решению.

Пример. Один банк обещает вкладчику прибыль 2% в месяц, а другой - 25% годовых. Куда выгоднее вложить деньги?

III . Отражение исторического аспекта

Задачи с «исторической» фабулой могут носить чье-то имя, отражать факты из жизни конкретных исторических личностей, содержать сведения из истории страны, науки, техники и др.

IV . Занимательность

На уроках математики нужны задачи и упражнения, которые оживили бы урок. Такие задачи с занимательным сюжетом развивают сообразительность, природную смекалку. Занимательность, заложенная в содержании задачи, особым образом окрашивает учебный материал, делает процесс решения более привлекательным, выступает эмоциональной основой, на которой создается положительное отношение к предмету.

Например:

По тропинке вдоль кустов Это вместе шли куда-то

Шло одиннадцать хвостов. Петухи и поросята.

Сосчитать я также смог, А теперь вопрос таков:

что шагало тридцать ног. Сколько было петухов?

И узнать я был бы рад,

Сколько было поросят?

V . Использование компьютерных технологий

• Обогащает урок эмоциональной окраской;
• Психологически облегчает процесс усвоения;
• Возбуждает живой интерес к предмету познания;
• Возрастает уровень использования наглядности на уроке;
• Повышает производительность труда учителя и учащихся на уроке.

Решение задач – основная составляющая урока.

ФАКТОРЫ, СВЯЗАННЫЕ С ОРГАНИЗАЦИЕЙ ДЕЯТЕЛЬНОСТИ ПО РЕШЕНИЮ ЗАДАЧИ

1. Осознание цели решения задачи

Наиболее осознанные мотивы деятельности возникают в том случае, когда ученик понимает цели деятельности. Поэтому при решении задач важна постановка цели решения конкретной задачи. Такими локальными целями могут быть : получение нового математического факта, подготовка к самостоятельной деятельности, проверка усвоения знаний, обобщение наблюдаемых в жизни явлений и перевод их на математический язык, необходимость новых знаний для решения практических задач и др.

II . Знание основных отношений и их свойств, заложенных в задаче

Для развития учебно-познавательных мотивов средством задач важно иметь подготовленную для решения задач почву, то есть учащиеся должны знать отношения и свойства отношений, заложенные в предлагаемую им задачу. Лишь посильное задание может привести к успеху, что выступает важнейшим стимулом познания. Однако, важно и то, каким трудом добыт успех. Слишком легкая работа не вызывает чувства удовлетворения. Трудное, но преодолимое, окрашивает деятельность ученика положительными эмоциями.

III . Математическое моделирование задачи

Математические модели могут быть алгебраическими (уравнения, неравенства, их различные системы), аналитическими (функции, дифференциальные уравнения, производные и др.), геометрическими (чертеж, рисунок, проекция трехмерного тела и др.), графическими (график функции, уравнения, неравенства, их системы и др.

Составление математической модели текстовой задачи, перевод реально происходящих в действительности процессов и явлений на язык математики, позволяет демонстрировать применение математики как инструмента, позволяющего математизировать реальные практические ситуации, отражая специфические особенности предмета. Важен выбор наиболее рациональной модели.

IV . Поиск решения задачи и его реализация

Поиск решения задачи один из существенно важных элементов процесса решения задачи. Обычно выделяют четыре этапа решения задачи

1. понимание постановки задачи,

2. составление плана решения;

3. осуществление плана;

4. изучение полученного решения.

Каждый учитель начинает работу не на пустом месте.

Лекции по педагогике и методике дают нам общее направление в работе.

Кроме того каждый из нас при обучении в школе видит живой пример своего учителя и на практике следует его опыту, учитывая его достоинства и недостатки.

Мне повезло: я работаю в коллективе математиков, каждый из которых имеет свой подчерк работы и у каждого есть чему поучиться.

Но я хочу никому подражать, я хочу творчески осмыслить все, что познаю и практически применяю.

Крупицы моих личных удач в преподавании математики, во взаимодействиях с каждым учеником – это те кирпичики, из которых строится мой опыт работы.