Презентация на тему: "Линейная и векторная алгебра"

ВЕКТОРНАЯ АЛГЕБРА

Основные определения

Векторы

Определение . Вектором назовём направленный отрезок, т.е. отрезок прямой, ограниченный двумя точками, одна из которых называется начальной, а другая конечной.

Изображение и обозначения

Компланарные векторы

Вектор, точка приложения которого может быть выбрана произвольно, называют свободным.

Линейные операции над векторами

К линейным операциям относятся операции умножения вектора на

число, сложения и вычитания векторов.

Свойства линейных операций над векторами

Линейная зависимость векторов. Аффинный базис

Базис на плоскости

Базис в трехмерном пространстве

Проекция вектора на ось

Теоремы о проекциях

Прямоугольный декартов базис

Длина вектора

Длина вектора, заданного концами – расстояние между точками

Направляющие косинусы вектора

Направление вектора в пространстве определяется углами α, β и γ между вектором и положительным направлением соответствующих осей координат ОХ, ОУ, ОZ; cos α, cos β и cos γ называются направляющими косинусами вектора.

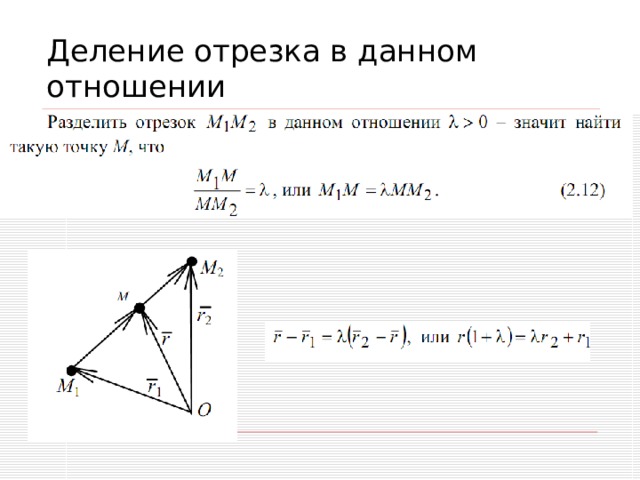
Деление отрезка в данном отношении

Скалярное произведение

Свойства скалярного произведения

Вычисление проекции вектора на вектор

Скалярное произведение в декартовой системе координат

Скалярное произведение орт

Скалярное произведение векторов равно сумме произведений их одноименных проекций

Итоговые формулы

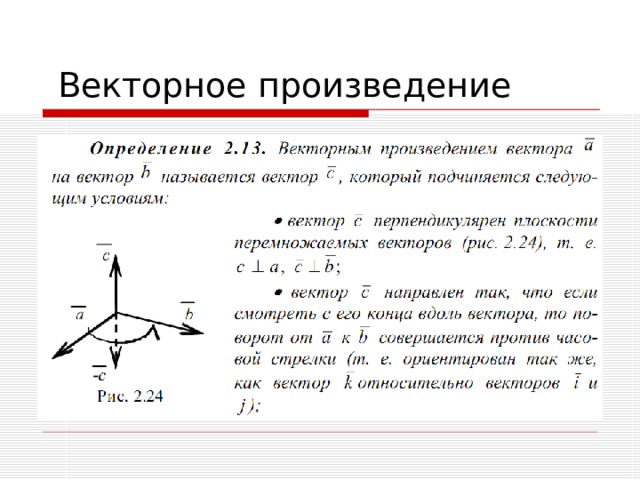
Векторное произведение

Модуль векторного произведения

Основные свойства векторного произведения

Векторное произведение в декартовой системе координат

Векторное произведение орт

С помощью определения векторного произведения можно решать задачу о вычислении площади треугольника, построенного на векторах как на сторонах (рис 2.26).

Смешанное произведение трёх векторов

Смешанное произведение в декартовой системе координат

Вычислим предварительно векторное произведение

Геометрический смысл смешанного произведения

Построим на векторах как на рёбрах параллелепипед

Вывод: модуль смешанного произведения трёх векторов равен объёму параллелепипеда, построенного на этих векторах как на рёбрах.

Свойства смешанного произведения

Все свойства смешанного произведения доказываются с помощью свойств определителя!

Условие компланарности трех векторов