Презентация на тему "Объемы"

ОБЪЕМ ФИГУР В ПРОСТРАНСТВЕ

Объем – величина, аналогичная площади и сопоставляющая фигурам в пространстве неотрицательные действительные числа. За единицу объема принимается куб, ребро которого равно единице измерения длины.

Для объемов пространственных фигур справедливы свойства, аналогичные свойствам площадей плоских фигур, а именно:

1. Объем фигуры в пространстве является неотрицательным числом.

2. Равные фигуры имеют равные объемы.

3. Если фигура Ф составлена из двух неперекрывающихся фигур Ф 1 и Ф 2 , то объем фигуры Ф равен сумме объемов фигур Ф 1 и Ф 2 , т.е.

V ( Ф )= V ( Ф 1 )+ V ( Ф 2 ).

Две фигуры, имеющие равные объемы, называются равновеликими.

В режиме слайдов ответы и решения появляются после кликанья мышкой

ОБЪЕМ ПАРАЛЛЕЛЕПИПЕДА

Объем пространственной фигуры характеризует величину части пространства, которую занимает эта фигура.

О бъем прямоугольного параллелепипеда равен произведению трех его измерений, т.е. если ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны a , b и c , то его объем V выражается формулой

В режиме слайдов формулировки появляются после кликанья мышкой

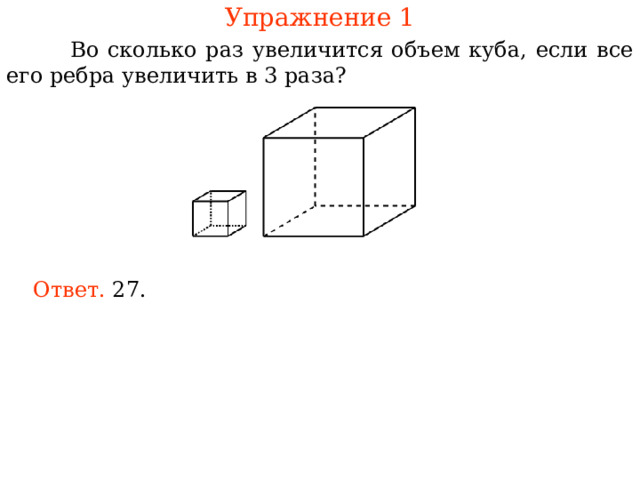
Упражнение 1

Во сколько раз увеличится объем куба, если все его ребра увеличить в 3 раза?

Ответ.

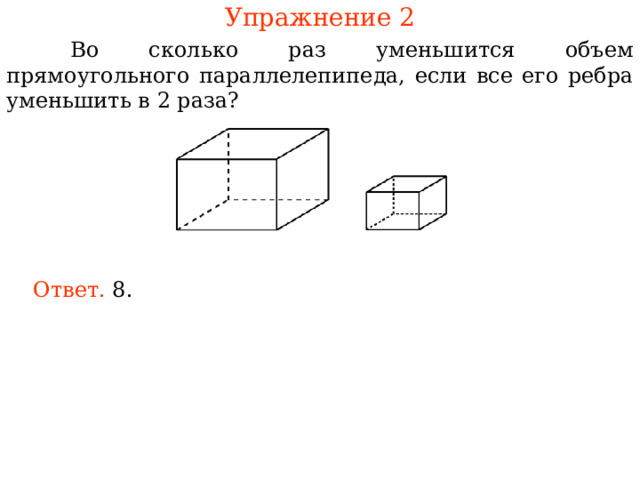
Упражнение 2

Во сколько раз уменьшится объем прямоугольного параллелепипеда, если все его ребра уменьшить в 2 раза?

Ответ.

Упражнение 3

Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 3. Каким должно быть третье ребро, выходящее из той же вершины, чтобы объем этого параллелепипеда равнялся 30?

В режиме слайдов ответы и решения появляются после кликанья мышкой

Ответ: 5.

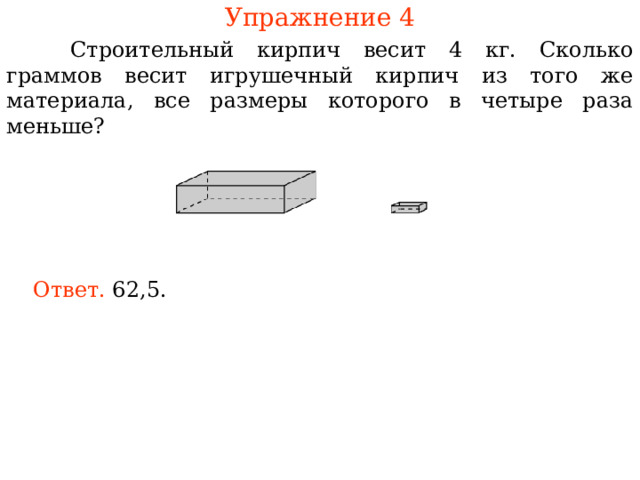
Упражнение 4

Строительный кирпич весит 4 кг. Сколько граммов весит игрушечный кирпич из того же материала, все размеры которого в четыре раза меньше?

Ответ.

Упражнение 5

Основанием аквариума является прямоугольник со сторонами 40 см и 50 см. Уровень воды в нем находится на высоте 80 см. Эту воду перелили в другой аквариум, основанием которого является прямоугольник со сторонами 80 см и 100 см. На какой высоте будет находиться уровень воды?

В режиме слайдов ответы и решения появляются после кликанья мышкой

Ответ: 20 см .

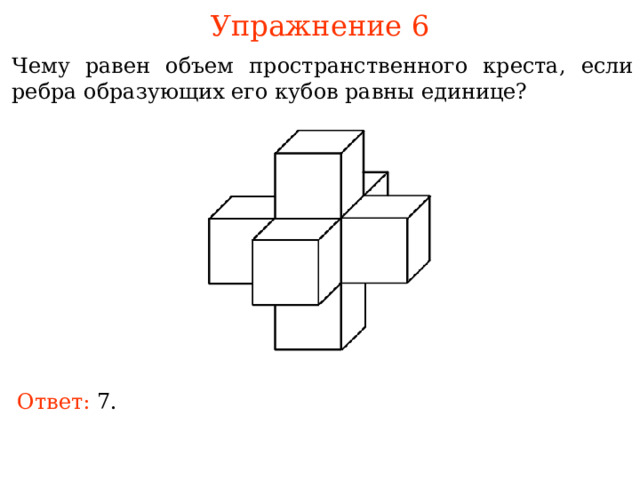
Упражнение 6

Чему равен объем пространственного креста, если ребра образующих его кубов равны единице?

В режиме слайдов ответы и решения появляются после кликанья мышкой

Ответ: .

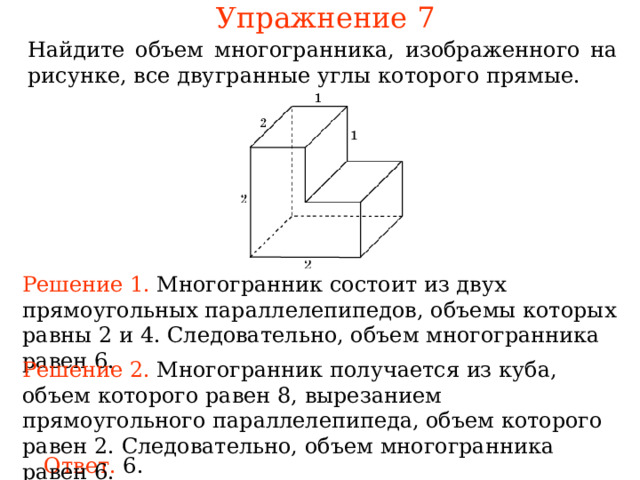
Упражнение 7

Найдите многогранника, изображенного на рисунке, все двугранные углы которого прямые.

Решение 1. ногогранник состоит из двух , равн . Следовательно, многогранника рав .

Решение 2. ногогранник Следовательно, многогранника рав .

Ответ.

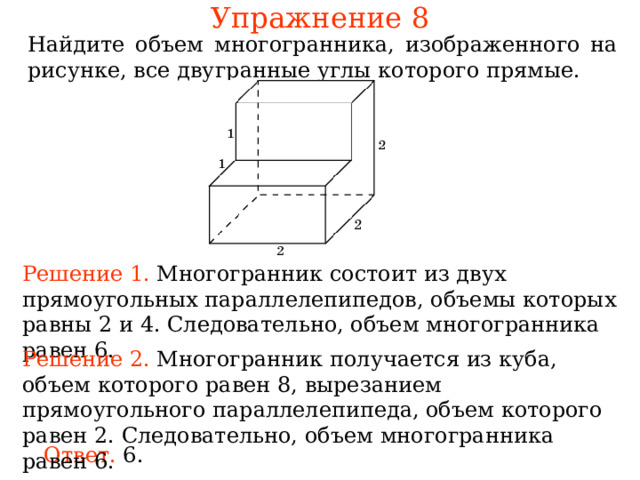
Упражнение 8

Найдите многогранника, изображенного на рисунке, все двугранные углы которого прямые.

Решение 1. ногогранник состоит из двух , равн . Следовательно, многогранника рав .

Решение 2. ногогранник Следовательно, многогранника рав .

Ответ.

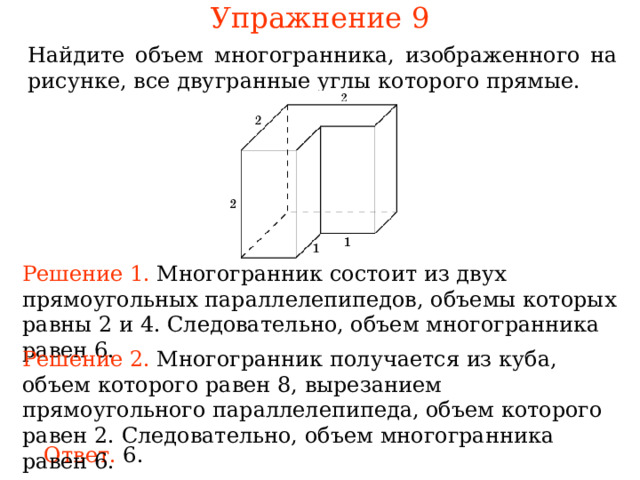
Упражнение 9

Найдите многогранника, изображенного на рисунке, все двугранные углы которого прямые.

Решение 1. ногогранник состоит из двух , равн . Следовательно, многогранника рав .

Решение 2. ногогранник Следовательно, многогранника рав .

Ответ.

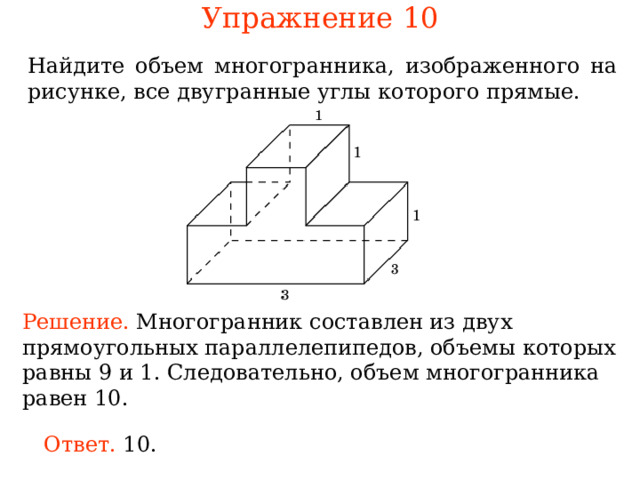
Упражнение 1 0

Найдите многогранника, изображенного на рисунке, все двугранные углы которого прямые.

Решение. ногогранник Следовательно, многогранника рав .

Ответ.

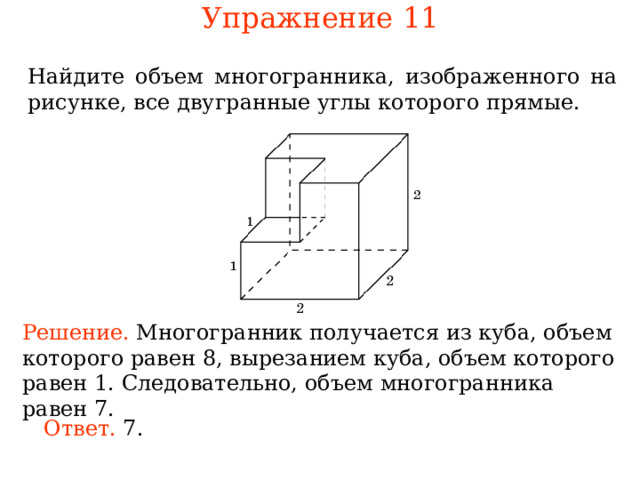
Упражнение 1 1

Найдите многогранника, изображенного на рисунке, все двугранные углы которого прямые.

Решение. ногогранник Следовательно, многогранника рав .

Ответ.

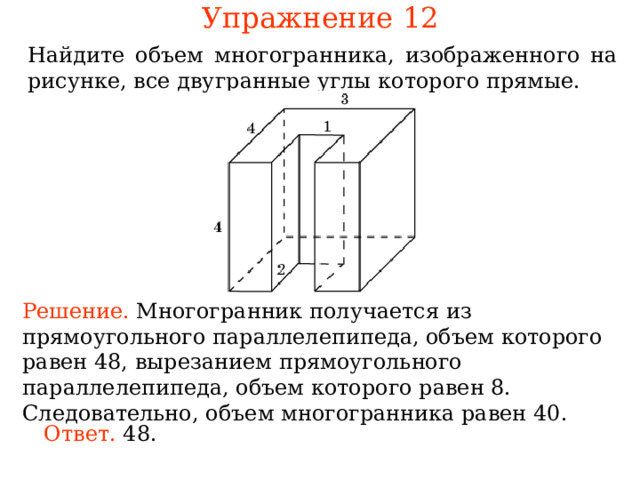
Упражнение 1 2

Найдите многогранника, изображенного на рисунке, все двугранные углы которого прямые.

Решение. ногогранник Следовательно, многогранника рав .

Ответ.

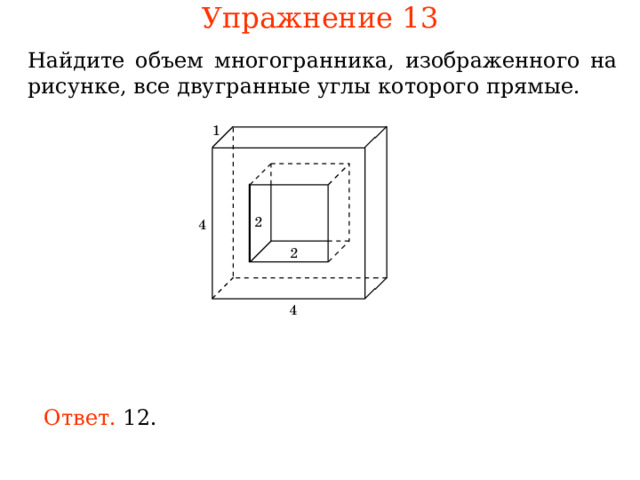
Упражнение 13

Найдите многогранника, изображенного на рисунке, все двугранные углы которого прямые.

Ответ.

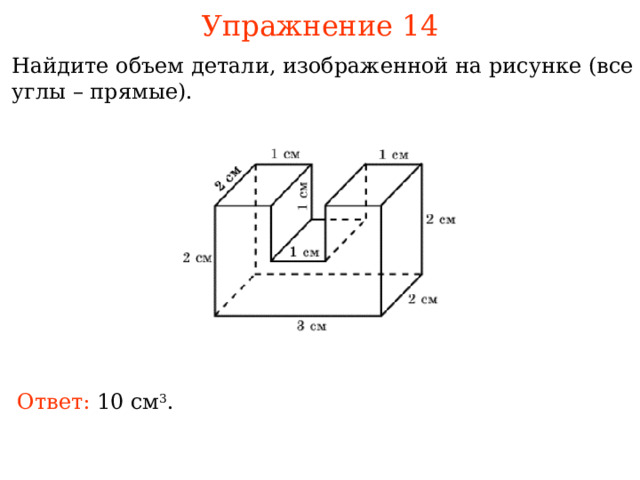
Упражнение 14

Найдите объем детали, изображенной на рисунке (все углы – прямые).

В режиме слайдов ответы и решения появляются после кликанья мышкой

Ответ: 0 см 3 .

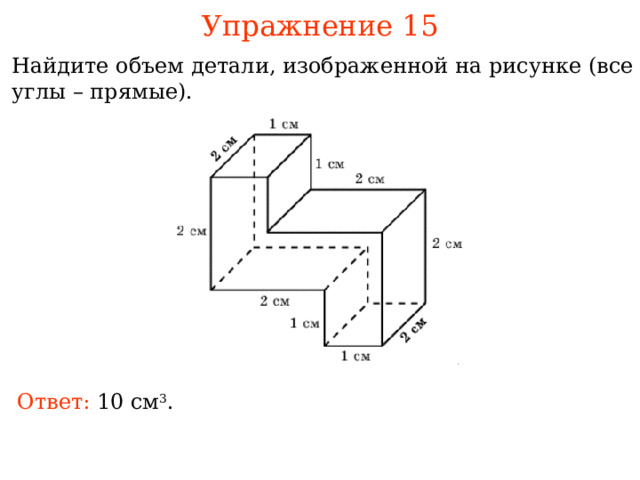
Упражнение 15

Найдите объем детали, изображенной на рисунке (все углы – прямые).

В режиме слайдов ответы и решения появляются после кликанья мышкой

Ответ: 0 см 3 .

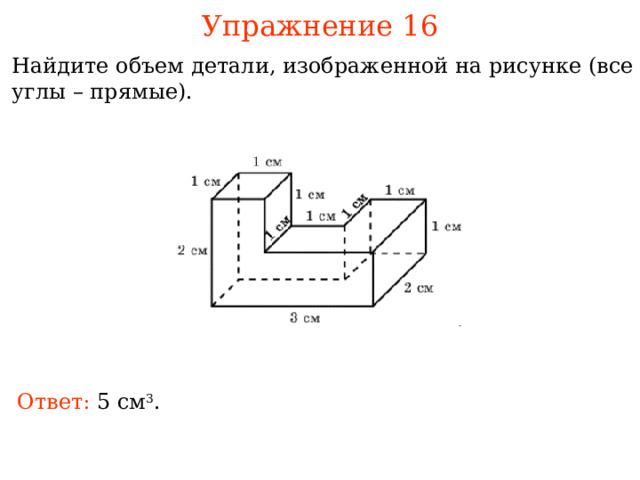
Упражнение 16

Найдите объем детали, изображенной на рисунке (все углы – прямые).

В режиме слайдов ответы и решения появляются после кликанья мышкой

Ответ: см 3 .

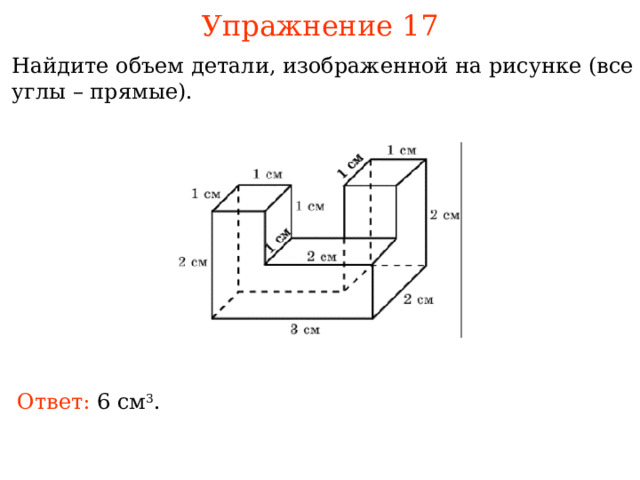
Упражнение 17

Найдите объем детали, изображенной на рисунке (все углы – прямые).

В режиме слайдов ответы и решения появляются после кликанья мышкой

Ответ: см 3 .

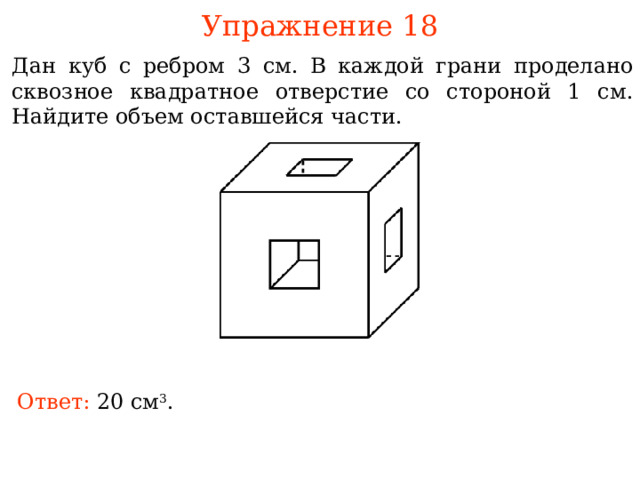
Упражнение 18

Дан куб с ребром 3 см. В каждой грани проделано сквозное квадратное отверстие со стороной 1 см. Найдите объем оставшейся части.

В режиме слайдов ответы и решения появляются после кликанья мышкой

Ответ: 20 см 3 .

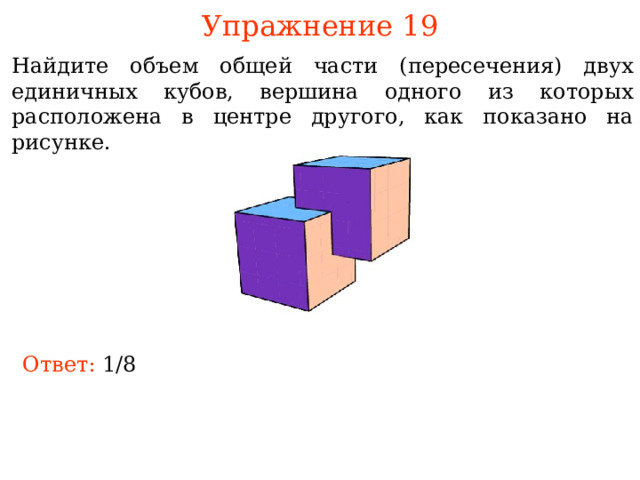
Упражнение 19

Найдите объем общей части (пересечения) двух единичных кубов, вершина одного из которых расположена в центре другого, как показано на рисунке.

В режиме слайдов ответы и решения появляются после кликанья мышкой

Ответ: 1/8

Упражнение 20

Найдите объем фигуры, составленной из двух единичных кубов, две вершины одного из которых расположены в центрах граней другого.

В режиме слайдов ответы и решения появляются после кликанья мышкой

Ответ: 1,75.

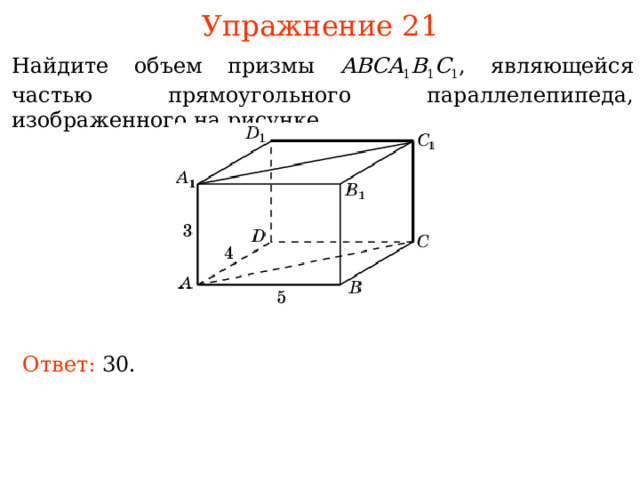
Упражнение 21

Найдите объем п ризмы ABCA 1 B 1 C 1 , являющейся частью прямоугольного параллелепипеда, изображенного на рисунке .

В режиме слайдов ответы и решения появляются после кликанья мышкой

Ответ: 30 .

Упражнение 22

Найдите объем п ризмы ABOA 1 B 1 O 1 , являющейся частью прямоугольного параллелепипеда, изображенного на рисунке .

В режиме слайдов ответы и решения появляются после кликанья мышкой

Ответ: 12.

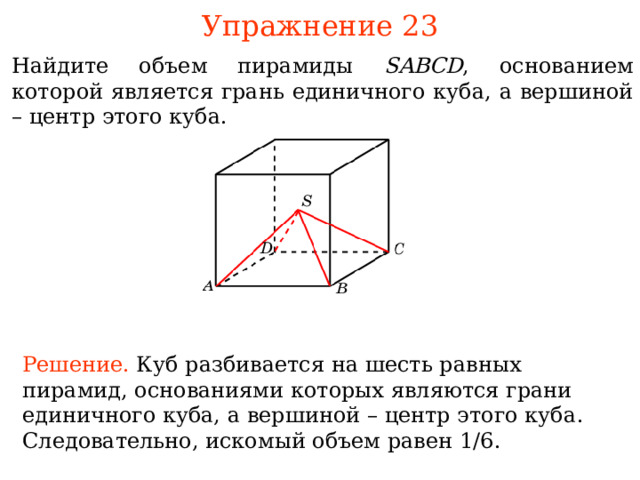
Упражнение 2 3

Найдите объем пирамиды SABCD , основанием которой является грань единичного куба, а вершиной – центр этого куба.

В режиме слайдов ответы и решения появляются после кликанья мышкой

Решение. Куб разбивается на шесть равных пирамид, основани ями котор ых явля ю тся гран и единичного куба, а вершиной – центр этого куба . Следовательно, искомый объем равен 1/6.

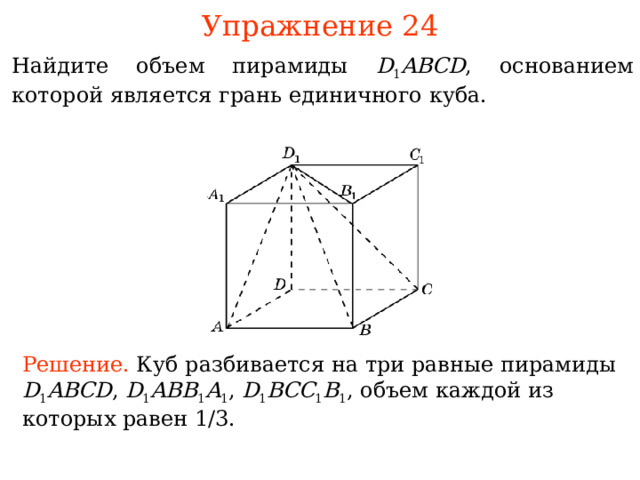
Упражнение 2 4

Найдите объем пирамиды D 1 ABCD , основанием которой является грань единичного куба.

В режиме слайдов ответы и решения появляются после кликанья мышкой

Решение. Куб разбивается на три равные пирамиды D 1 ABCD , D 1 ABB 1 A 1 , D 1 BCC 1 B 1 , объем каждой из которых равен 1 /3.

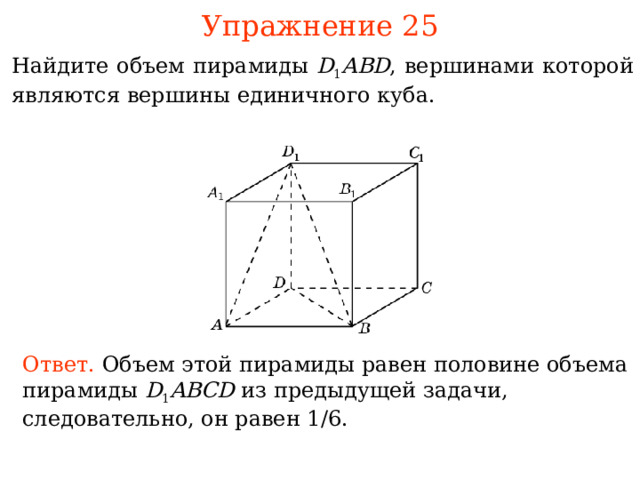
Упражнение 2 5

Найдите объем пирамиды D 1 ABD , вершинами которой явля ю тся вершины единичного куба.

В режиме слайдов ответы и решения появляются после кликанья мышкой

Ответ. Объем этой пирамиды равен половине объема пирамиды D 1 ABCD из предыдущей задачи, следовательно, он равен 1 / 6 .