Презентация на тему: "Теорема Пифагора" (8 класс)

Пифагор Самосский (6 век до н.э.)

Древнегреческий философ, политический деятель, математик. Пифагору приписывается изучение свойств целых чисел, пропорций и доказательства знаменитой теоремы Пифагора.

Содержание

• Пифагор Самосский

2. Способы доказательства теоремы

3. История открытия теоремы

4. Применение теоремы

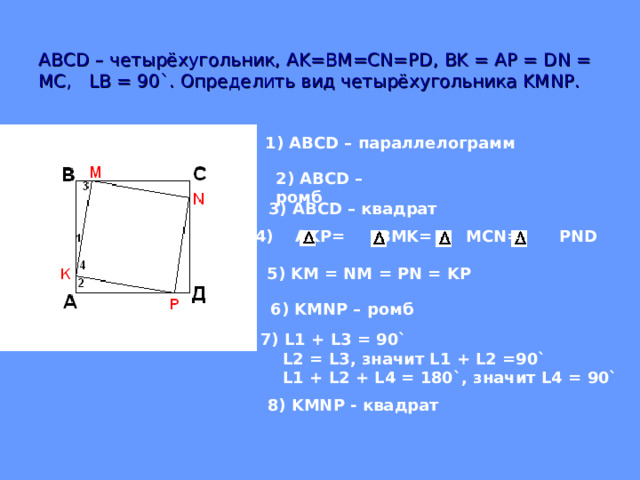
АВС D – четырёхугольник, AK=BM=CN=PD , BK = AP = DN = MC , LB = 90` . Определить вид четырёхугольника KMNP.

1) ABCD – параллелограмм

2) ABCD – ромб

• AKP = BMK= MCN= PND

3) ABCD – квадрат

5) KM = NM = PN = KP

6) KMNP – ромб

7) L1 + L3 = 90`

L2 = L3 , значит L1 + L2 =90`

L1 + L2 + L4 = 180` , значит L4 = 90`

8) KMNP - квадрат

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

c

b

b

b

a

a

a

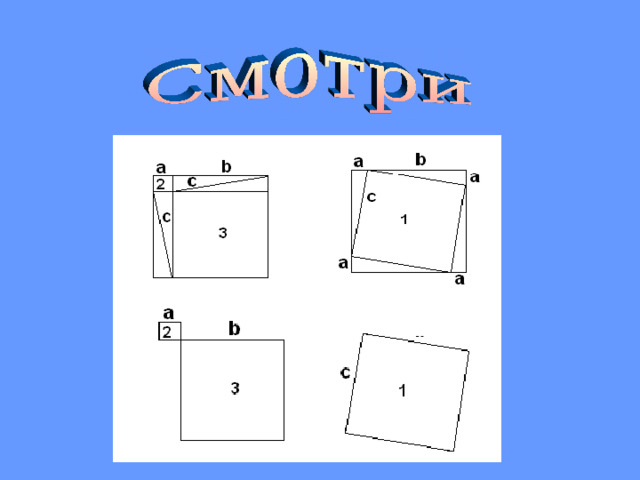
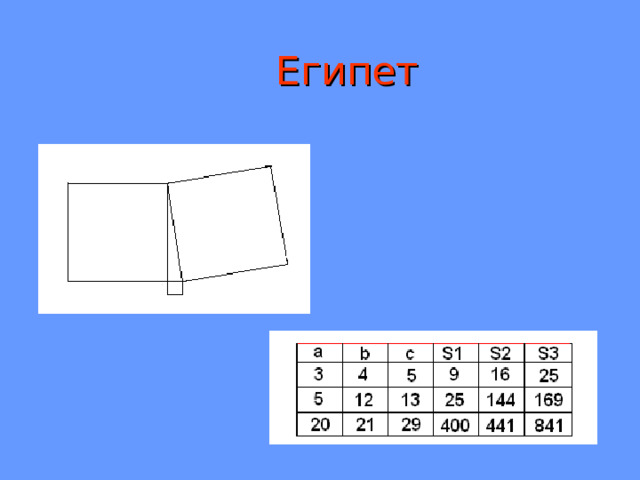
Египет

Теорема Пифагора ( доказательство Гарфилда)

Дано:

АВС;

LC = 90`

а, b – катеты

с – гипотенуза

Доказать:

c 2 = a 2 + b 2

• ВС D К – трапеция. S = ½ (a + b) (a + b) = ½ (a + b) 2

2 .Трапеция состоит из двух равных треугольников АВС и АК D и

треугольника АВК. S = 2* ½ ab + ½ c 2

3. ½ (a + b) 2 = 2* ½ ab + ½ c 2

4. (a + b) 2 = 2ab + c 2

5. c 2 = a 2 + b 2

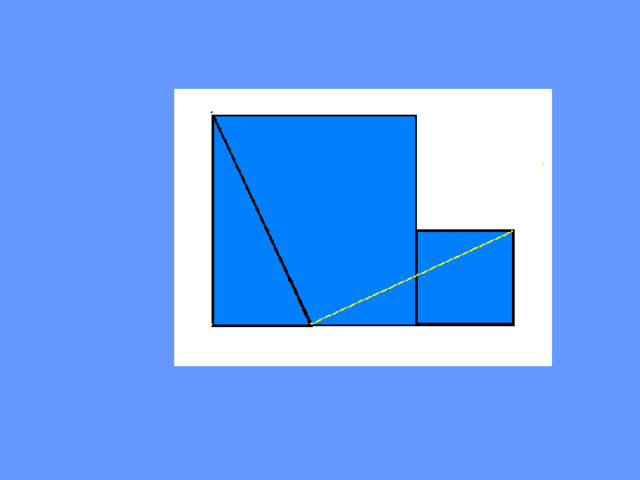
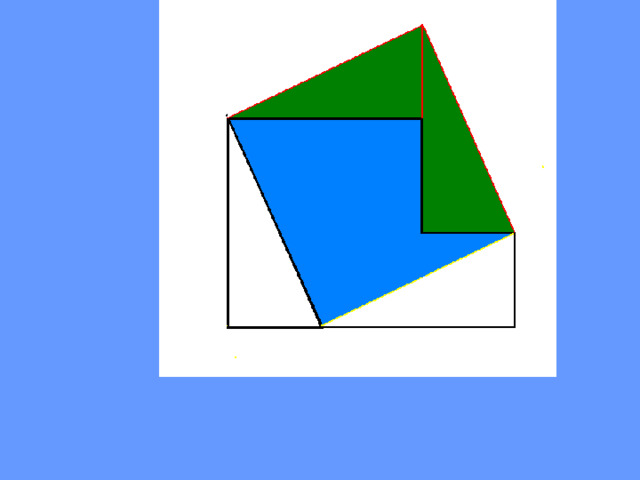
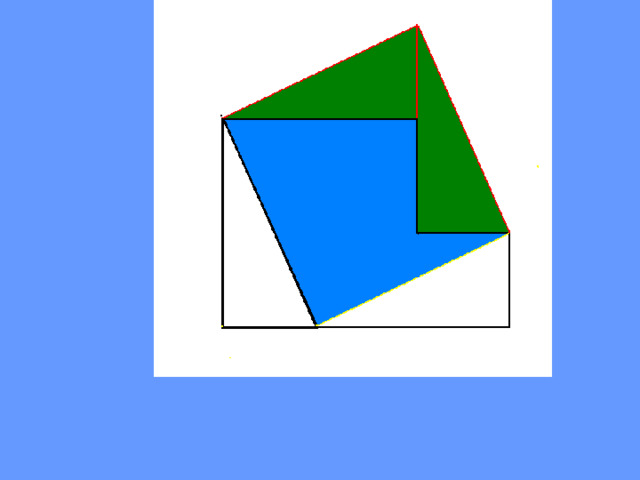
Считается, что эта теорема не была открыта Пифагором, одни полагают,

что Пифагор первым дал ее полноценное доказательство, другие отказывают ему в этой заслуге. Легенда сообщает, что в честь этого открытия Пифагор принес в жертву сто быков.

Сонет Шамиссо.

Пребудет вечной истина, как скоро Её познает слабый человек! И ныне теорема Пифагора Верна, как и в его далёкий век. Обильно было жертвоприношенье Богам от Пифагора. Сто быков Он отдал на закланье и сожженье За света луч, пришедший с облаков. Поэтому всегда с тех самых пор, Чуть истина рождается на свет, Быки ревут, её почуяв, вслед. Они не в силах свету помешать, А могут лишь закрыв глаза дрожать От страха, что вселил в них Пифагор.

Формулировки теоремы Пифагора

"В прямоугольном треугольнике квадрат стороны, натянутой над прямым углом, равен квадратам на сторонах, заключающих прямой угол". (Евклид)

"Во всяком прямоугольном треугольнике квадрат, образованный на стороне, натянутой над прямым углом, равен сумме двух квадратов, образованных на двух сторонах, заключающих прямой угол". (Аннариции)

"В прямоугольных треугольниках квадрат из стороны, противолежащей прямому углу, равен сумме квадратов из сторон, содержащих прямой угол". Петрушевский)

"Итак, площадь квадрата, измеренного по длинной стороне, столь же велика, как у двух квадратов, которые измерены по двум сторонам его, примыкающим к прямому углу". (около 1400 г.)

Мнемоническое правило теоремы

Если дан нам треугольник

И притом с прямым углом,

То квадрат гипотенузы

Мы всегда легко найдем:

Катеты в квадрат возводим,

Сумму степеней находим

И таким простым путем

К результату мы придем.

История открытия теоремы Пифагора

Индия

В Индии теорема Пифагора была известна около 18 в. до н.э.

История открытия теоремы

Пифагора

В древнем Китае

В математической книге Чу-пей говорится о пифагоровых

треугольниках со сторонами 3,4 и 5.

История открытия теоремы Пифагора

Египет и Вавилон

Египтянам (2300 г. до н.э.) было известно, что 3 2 +4 2 =5 2

(согласно папирусу Берлинского музея.

Вавилоняне (2000 г. до н.э.) смогли находить приближенно значение

гипотенузы прямоугольного треугольника.

История открытия теоремы Пифагора

В России перевод теоремы Пифагора был впервые сделан

Ф.И. Петрушевским.

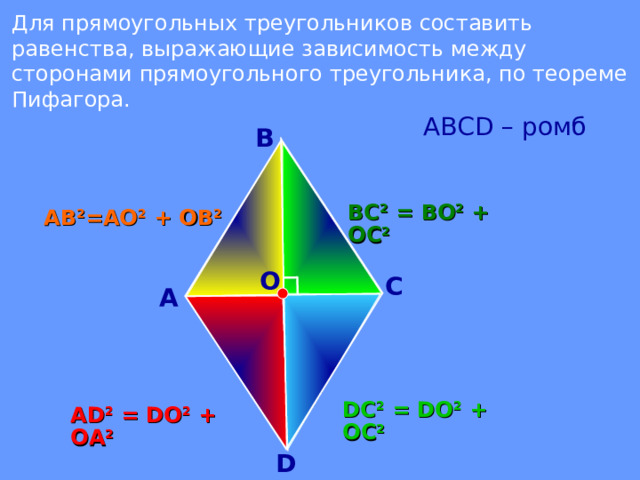
Для прямоугольных треугольников составить равенства, выражающие зависимость между сторонами прямоугольного треугольника, по теореме Пифагора.

АВС D – ромб

В

ВС 2 = ВО 2 + ОС 2

АВ 2 =АО 2 + ОВ 2

О

С

А

DC 2 = DO 2 + OC 2

А D 2 = DO 2 + OA 2

D

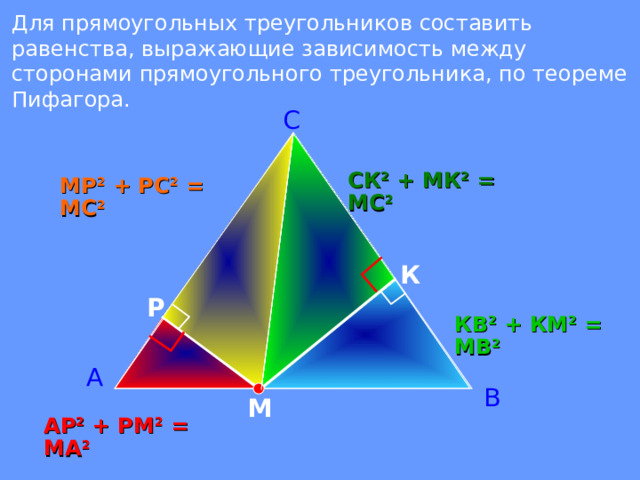
Для прямоугольных треугольников составить равенства, выражающие зависимость между сторонами прямоугольного треугольника, по теореме Пифагора.

С

СК 2 + МК 2 = МС 2

МР 2 + РС 2 = МС 2

К

Р

КВ 2 + КМ 2 = МВ 2

А

В

М

АР 2 + РМ 2 = МА 2

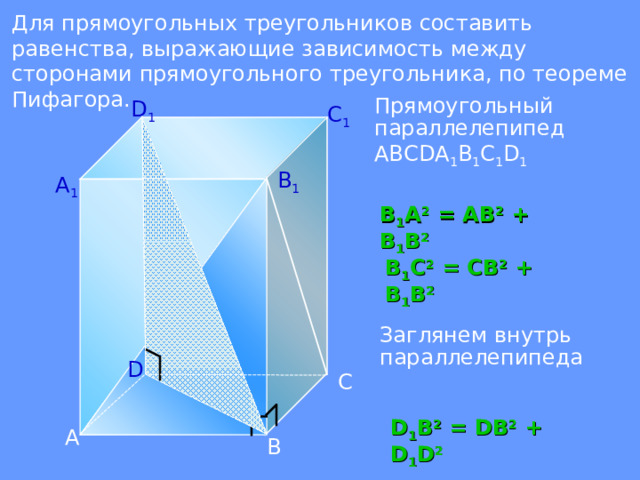
Для прямоугольных треугольников составить равенства, выражающие зависимость между сторонами прямоугольного треугольника, по теореме Пифагора.

Прямоугольный параллелепипед АВС D А 1 В 1 С 1 D 1

D 1

C 1

B 1

А 1

В 1 А 2 = АВ 2 + В 1 В 2

В 1 С 2 = СВ 2 + В 1 В 2

При работе с данным слайдом, необходима каркасная модель прямоугольного параллелепипеда. С помощью красной толстой нити, я моделирую эти треугольники.

Заглянем внутрь параллелепипеда

D

С

D 1 B 2 = D В 2 + D 1 D 2

А

В

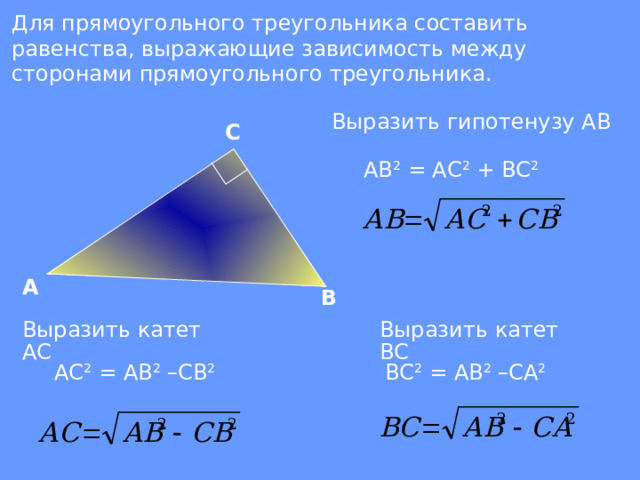
Для прямоугольного треугольника составить равенства, выражающие зависимость между сторонами прямоугольного треугольника.

Выразить гипотенузу АВ

С

АВ 2 = АС 2 + ВС 2

А

В

Выразить катет АС

Выразить катет ВС

АС 2 = АВ 2 –СВ 2

ВС 2 = АВ 2 –СА 2

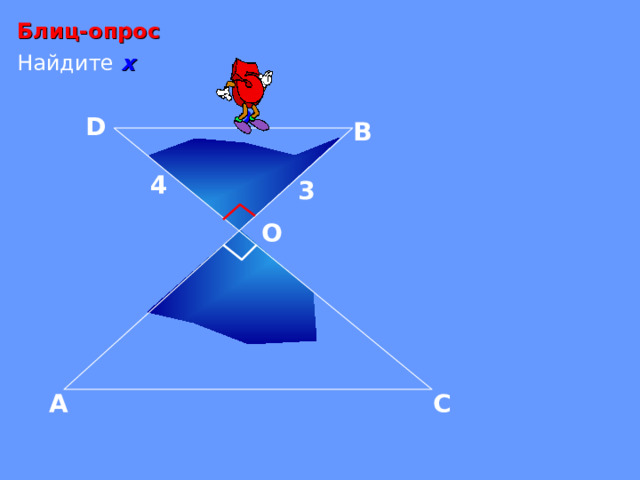
Блиц-опрос

Найдите х

х

D

В

4

3

О

«Упражнения по планиметрии на готовых чертежах» С.М. Саврасова, Г.А. Ястребинецкий.

С

А

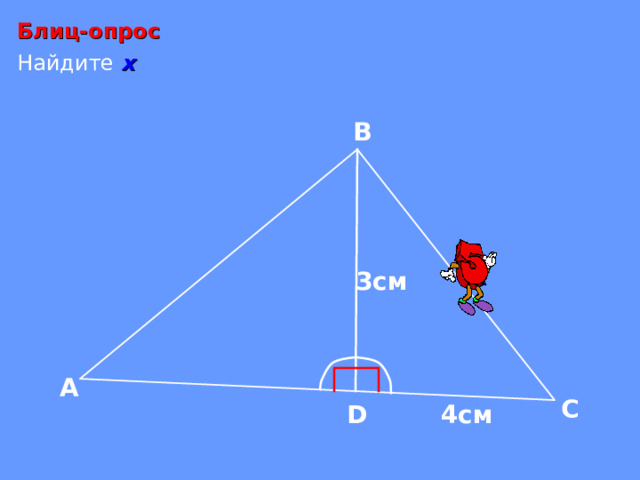
Блиц-опрос

Найдите х

В

х

3см

«Упражнения по планиметрии на готовых чертежах» С.М. Саврасова, Г.А. Ястребинецкий.

А

С

D

4см

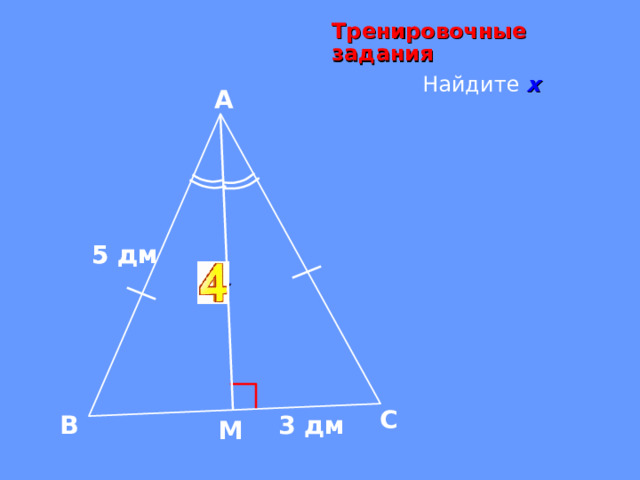
Тренировочные задания

Найдите х

А

5 дм

5 дм

х

«Упражнения по планиметрии на готовых чертежах» С.М. Саврасова, Г.А. Ястребинецкий.

С

3 дм

В

М

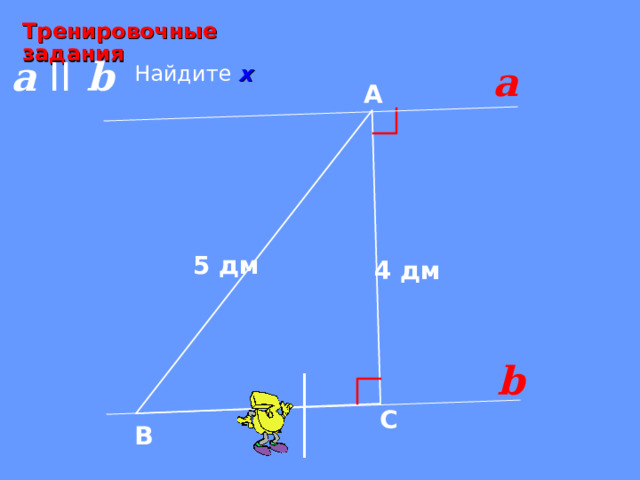
Тренировочные задания

a II b

a

Найдите х

А

5 дм

4 дм

«Упражнения по планиметрии на готовых чертежах» С.М. Саврасова, Г.А. Ястребинецкий.

b

х

С

В

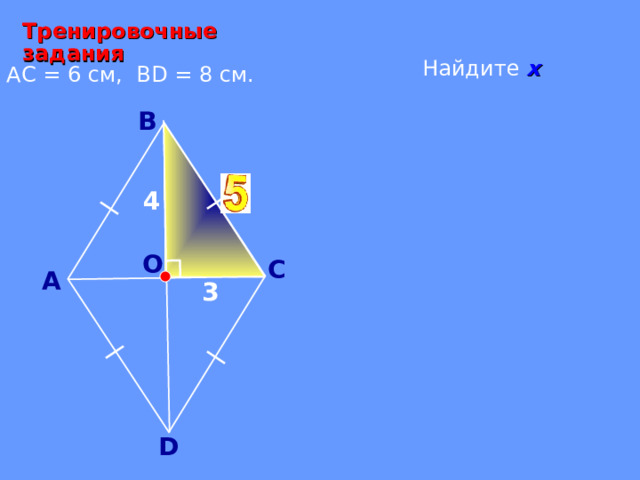
Тренировочные задания

Найдите х

АС = 6 см, В D = 8 см.

В

х

4

О

С

А

3

«Упражнения по планиметрии на готовых чертежах» С.М. Саврасова, Г.А. Ястребинецкий.

D

31

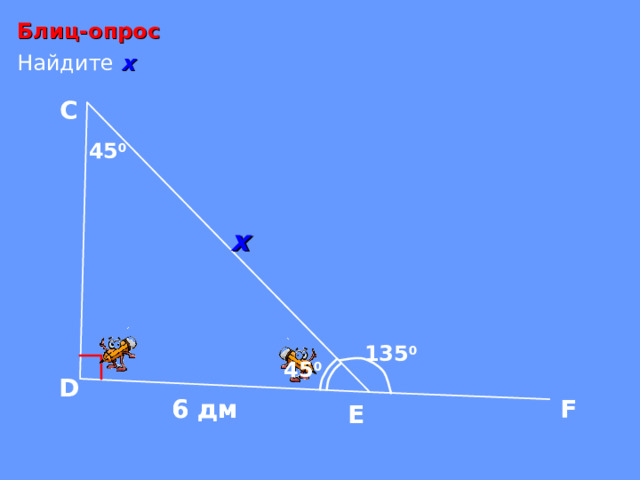
Блиц-опрос

Найдите х

С

4 5 0

х

«Упражнения по планиметрии на готовых чертежах» С.М. Саврасова, Г.А. Ястребинецкий.

135 0

45 0

D

6 дм

F

6 дм

E

31

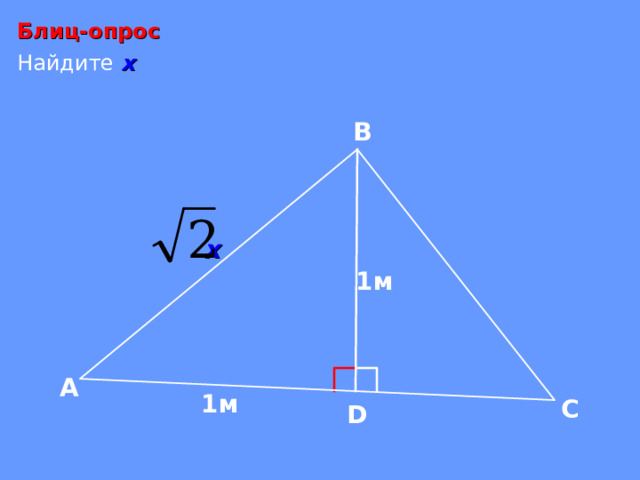
Блиц-опрос

Найдите х

В

х

1м

«Упражнения по планиметрии на готовых чертежах» С.М. Саврасова, Г.А. Ястребинецкий.

А

1м

С

D

31

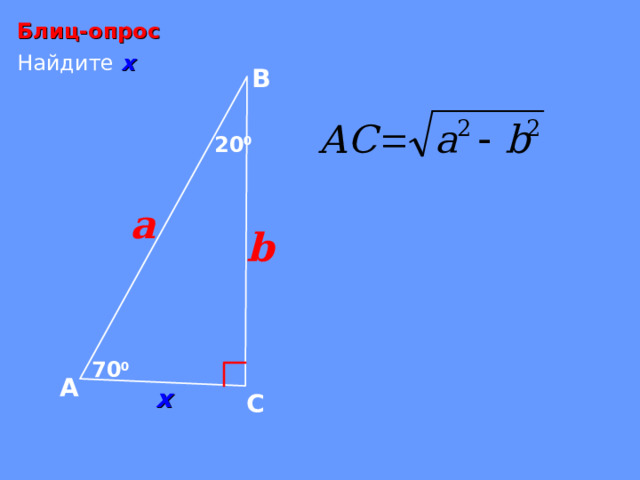
Блиц-опрос

Найдите х

В

20 0

a

b

«Упражнения по планиметрии на готовых чертежах» С.М. Саврасова, Г.А. Ястребинецкий.

70 0

А

х

С

31

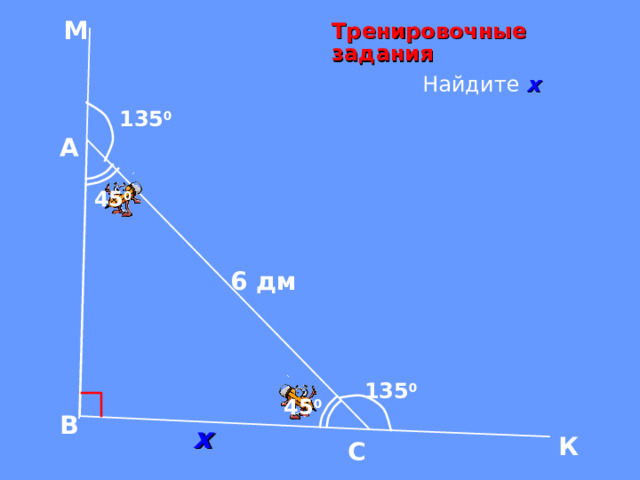
М

Тренировочные задания

Найдите х

135 0

А

45 0

6 дм

«Упражнения по планиметрии на готовых чертежах» С.М. Саврасова, Г.А. Ястребинецкий.

135 0

45 0

В

х

К

С

31

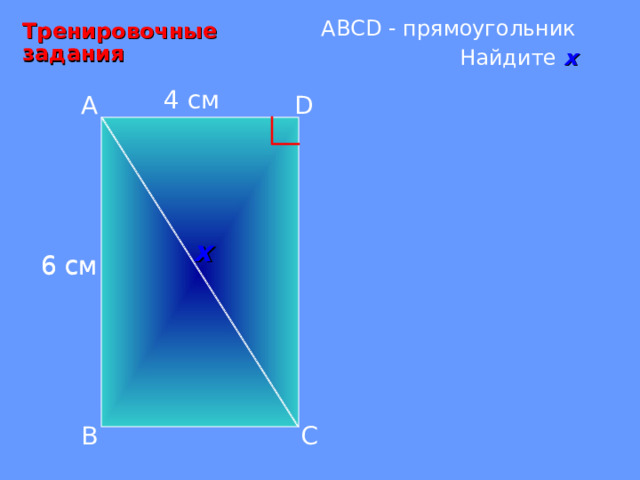
А BCD - прямоугольник

Тренировочные задания

Найдите х

4 см

A

D

х

6 см

6 см

«Упражнения по планиметрии на готовых чертежах» С.М. Саврасова, Г.А. Ястребинецкий.

B

C

31

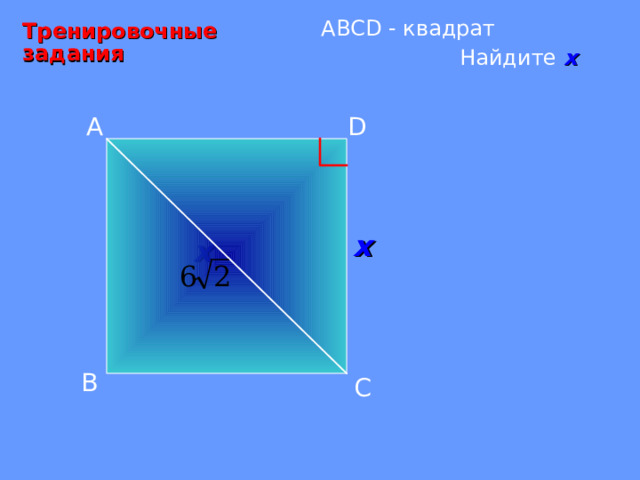
А BCD - квадрат

Тренировочные задания

Найдите х

A

D

х

х

х

«Упражнения по планиметрии на готовых чертежах» С.М. Саврасова, Г.А. Ястребинецкий.

B

C

31

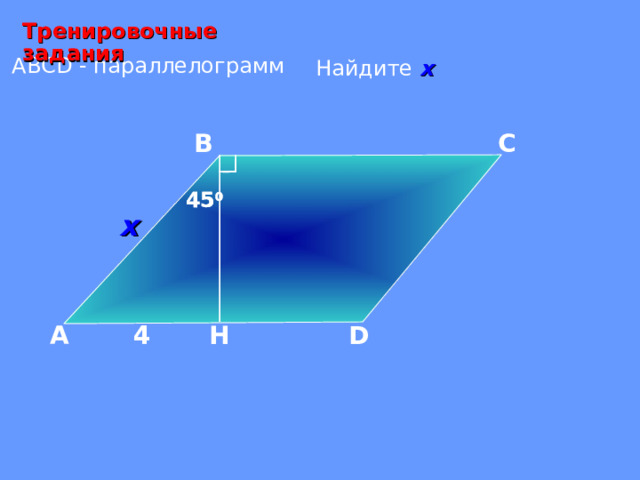
Тренировочные задания

А BCD - параллелограмм

Найдите х

В

С

45 0

45 0

х

«Упражнения по планиметрии на готовых чертежах» С.М. Саврасова, Г.А. Ястребинецкий.

H

4

А

D

4

31

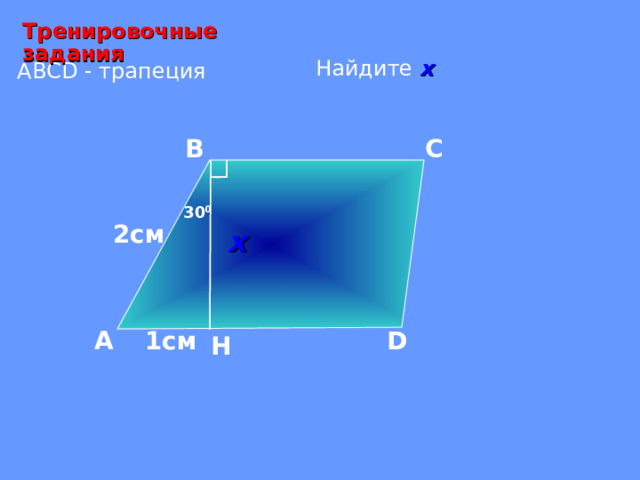
Тренировочные задания

А BCD - трапеция

Найдите х

В

С

30 0

2см

х

«Упражнения по планиметрии на готовых чертежах» С.М. Саврасова, Г.А. Ястребинецкий.

А

D

1см

H

31

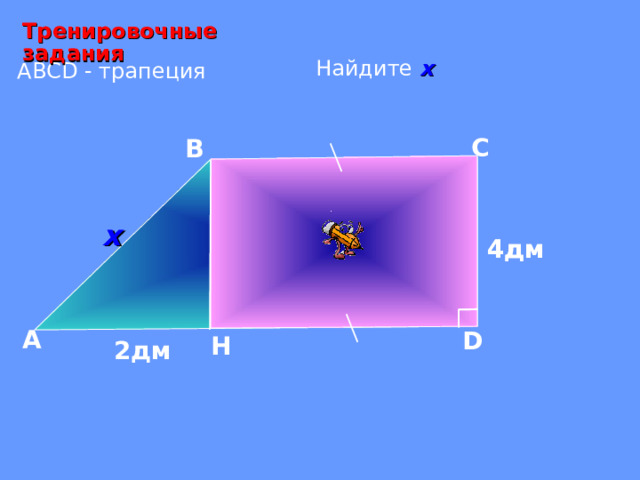
Тренировочные задания

Найдите х

А BCD - трапеция

С

В

х

4дм

4дм

«Упражнения по планиметрии на готовых чертежах» С.М. Саврасова, Г.А. Ястребинецкий.

А

D

H

2дм

31

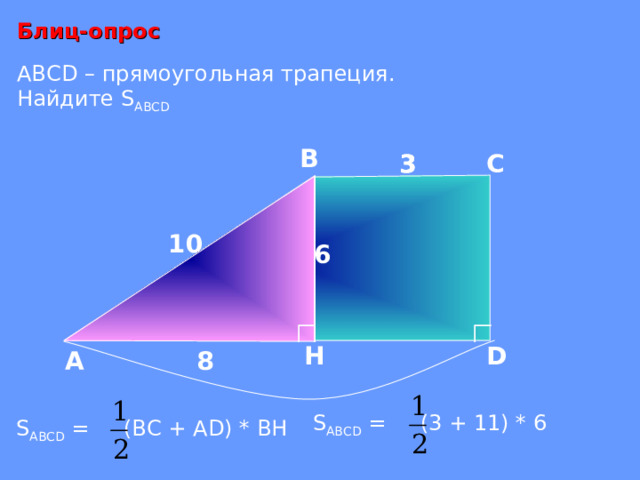
Блиц-опрос

ABCD – прямоугольная трапеция.

Найдите S ABCD

В

С

3

3

10

6

D

H

8

А

S ABCD = (3 + 11) * 6

S ABCD = (ВС + AD ) * ВН

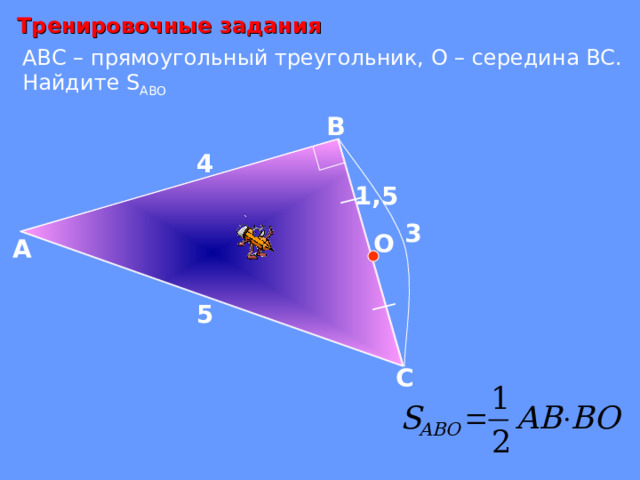
Тренировочные задания

АВС – прямоугольный треугольник, О – середина ВС.

Найдите S AB О

В

4

1,5

3

О

А

5

С

H

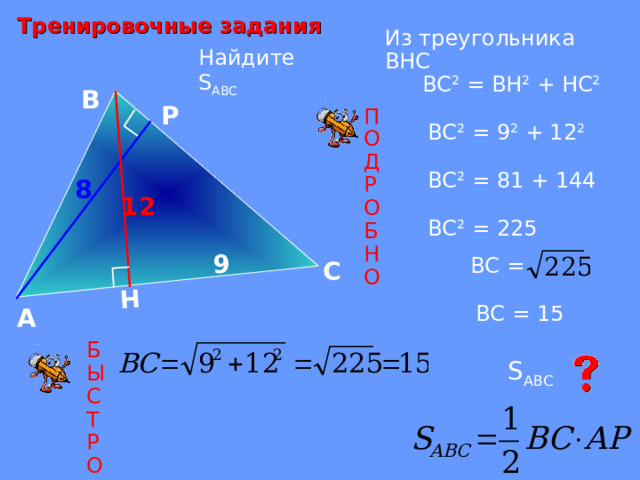
Тренировочные задания

Из треугольника ВНС

Найдите S ABC

ВС 2 = ВН 2 + НС 2

В

Р

П

О

Д

Р

О

Б

Н

О

ВС 2 = 9 2 + 12 2

ВС 2 = 81 + 144

8

12

ВС 2 = 225

9

ВС =

С

А

ВС = 15

Б

Ы

С

Т

Р

О

S АВС

43

Шаржи к теореме Пифагора

Пифагоровы штаны во все стороны равны.

Старинные задачи

Задача из учебника «Арифметика»

Леонтия Филипповича Магницкого

Случися некоему человеку к стене лествицу прибрати, стены же тоя высота есть 117 стоп. И обрете лествицу долготою 125 стоп. И ведати хощет, колико стоп сея лествицы нижний конец от стены отстояти имать .

Старинные задачи

У одного арабского математика XI века находим следующую задачу.

Птицы у реки

  На обоих берегах реки растет по пальме, одна против другой. Высота одной—30 локтей, другой— 20 локтей; расстояние между их основаниями— 50 локтей. На верхушке каждой пальмы сидит птица. Внезапно обе птицы заметили рыбу, выплывшую к поверхности воды между пальмами; они кинулись к ней разом и достигли ее одновременно. На каком расстоянии от основания более высокой пальмы появилась рыба ?

Старинные задачи

Над озером тихим,

с полфута размером,

высился лотоса цветок.

Он рос одиноко

И ветер порывом

отнес его в сторону.

Нет более цветка над водой.

Нашел же рыбак его ранней весной

В двух футах от места, где рос.

Итак, предложу я вопрос:

«Как озера вода здесь глубока?»

Софизм

Катет равен гипотенузе.

Доказательство: Пусть ВО –биссектриса угла В, Д-середина катета АС, ДО  АС, ОЕ  ВС,О F  ВА. Т.к.точка О расположена на биссектрисе угла В, то треугольники В F О и ВЕО равны по гипотенузе и острому углу. Поэтому

В F  ВЕ (1)

Далее, ОА = ОС, ибо каждая точка перпендикулярна от­резку АС, проходящему через середину АС, равноудалена от А и С. Так как OF = OE, то Д AOF = Д СОЕ, и поэтому

AF-CE (2)

Складывая почленно равенства (1) и (2), получим АВ = СВ, т. е. катет равен гипотенузе. Если ребята дога­даются, что точка О не может быть внутри треугольника АВС, тогда можно показать ,что если О вне треугольника АВС или на его стороне, то опять АВ  СВ.

Пифагор зажег и высоко поднял тот факел, который, как олимпийская эстафета, передается от поколения к поколению уже много веков.