Презентация на тему: "ВЕКТОРНАЯ АЛГЕБРА"

Векторная алгебра

Термин вектор

(от лат. Vector -“несущий “) впервые появился в 1845 г. у ирландского математика Уильяма Гамильтона

Уи́льям Ро́уэн Га́мильтон

1805 — 1865

выдающийся ирландский математик и физик XIX века.

§ 1. Определение вектора.

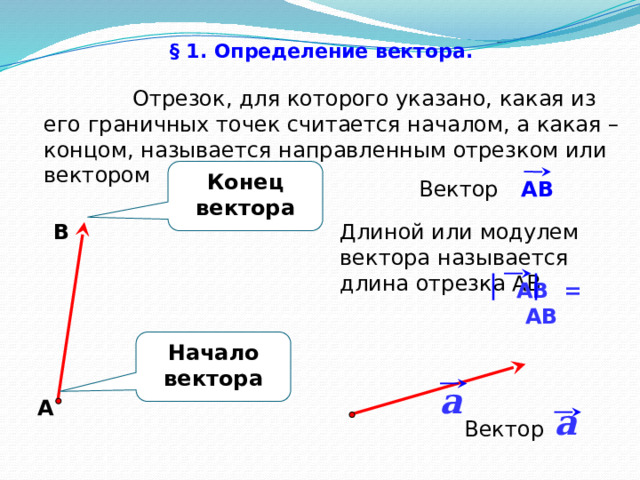
Отрезок, для которого указано, какая из его граничных точек считается началом, а какая – концом, называется направленным отрезком или вектором

Конец вектора

Вектор

АВ

Длиной или модулем вектора называется длина отрезка АВ

В

АВ = АВ

Начало вектора

a

А

a

Вектор

2

§ 1. Определение вектора.

Любая точка плоскости также является вектором.

В этом случае вектор называется нулевым

MM

Вектор

M

0

Вектор

Начало нулевого вектора совпадает с его концом, поэтому нулевой вектор не имеет какого-либо определенного направления. Иначе говоря, любое направление можно считать направлением нулевого вектора.

«Геометрия 7-9» Л.С. Атанасян и др.

Длина нулевого считается равной нулю

MM = 0

3

§ 1. Определение вектора.

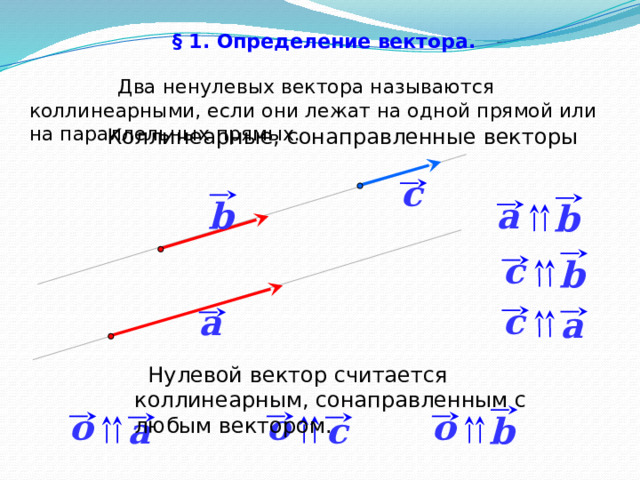
Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.

Коллинеарные, сонаправленные векторы

c

b

a

b

c

b

c

a

a

«Геометрия 7-9» Л.С. Атанасян и др.

Нулевой вектор считается коллинеарным, сонаправленным с любым вектором.

o

o

o

b

c

a

4

§ 1. Определение вектора.

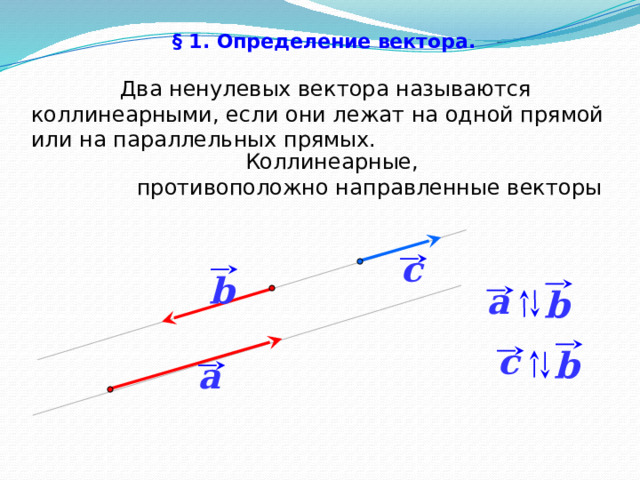
Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.

Коллинеарные,

противоположно направленные векторы

c

b

a

b

«Геометрия 7-9» Л.С. Атанасян и др.

c

b

a

5

§ 1. Определение вектора.

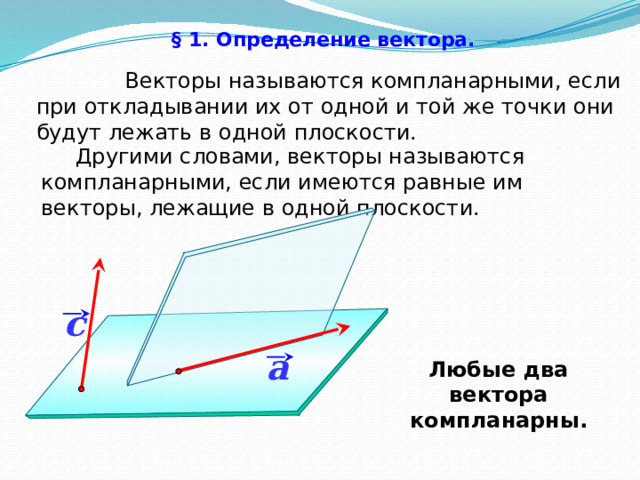
Векторы называются компланарными, если при откладывании их от одной и той же точки они будут лежать в одной плоскости.

Другими словами, векторы называются компланарными, если имеются равные им векторы, лежащие в одной плоскости.

c

«Геометрия 10-11» Л.С. Атанасян и др.

a

Любые два вектора компланарны.

6

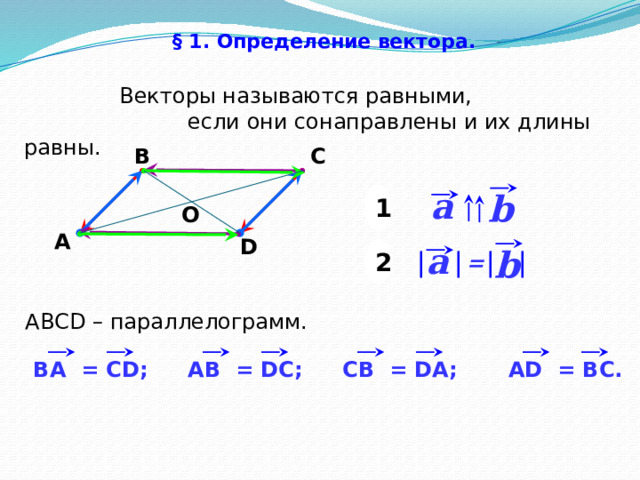
§ 1. Определение вектора.

Векторы называются равными,

если они сонаправлены и их длины равны.

С

В

a

b

1

О

А

D

a

b

2

=

АВСD – параллелограмм.

«Геометрия 7-9» Л.С. Атанасян и др.

CВ = DA;

AВ = DC;

ВA = CD;

AD = BC.

7

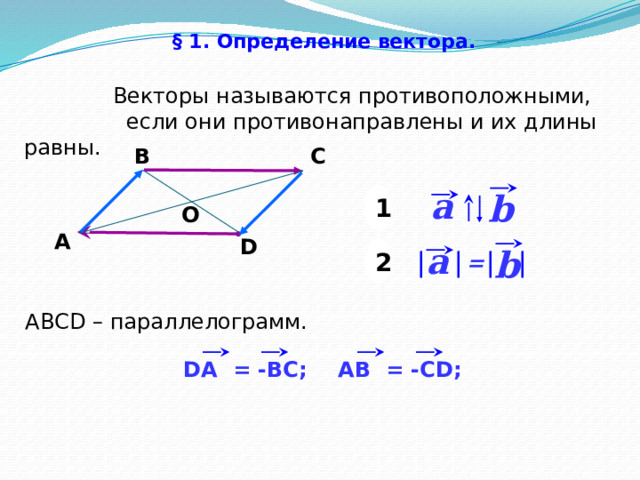
§ 1. Определение вектора.

Векторы называются противоположными,

если они противонаправлены и их длины равны.

С

В

a

b

1

О

А

D

a

b

2

=

АВСD – параллелограмм.

«Геометрия 7-9» Л.С. Атанасян и др.

AВ = -CD;

DA = -BC;

8

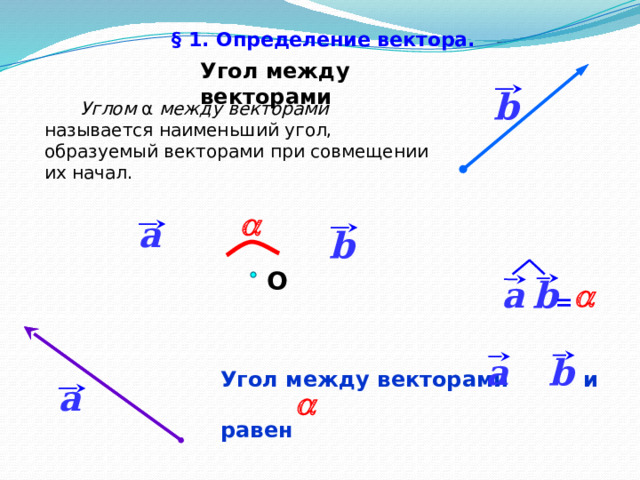
§ 1. Определение вектора.

Угол между векторами

b

Углом α между векторами называется наименьший угол, образуемый векторами при совмещении их начал.

a

a

b

О

b

a

a

=

a

b

Угол между векторами и

равен

a

a

9

§ 1. Определение вектора.

Для коллинеарных векторов

или

Два вектора называются ортогональными ,

если угол между ними равен 90 0 .

c

b

c

^

b

10

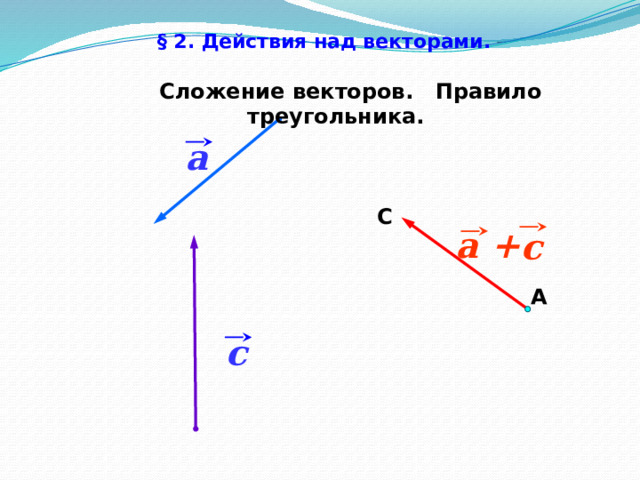
§ 2. Действия над векторами.

Сложение векторов. Правило треугольника.

a

С

a +

c

А

c

11

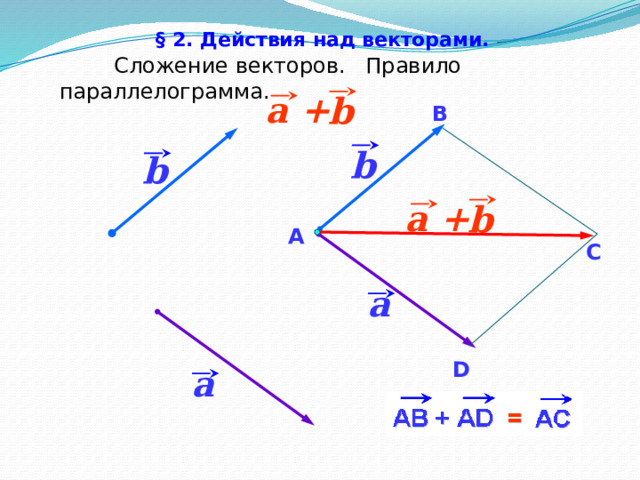
§ 2. Действия над векторами.

Сложение векторов. Правило параллелограмма.

a +

b

В

b

b

a +

b

А

C

a

D

a

12

§ 2. Действия над векторами.

Сложим первые две силы F 1 и F 2 (аксиома параллелограмма).

Количество сил уменьшилось на единицу.

Сложим полученную равнодействующую R 12 со следующей силой F 3 .

Количество сил вновь уменьшилось на единицу.

Повторим эту же операцию со следующей силой F 4 .

Осталась всего одна сила, эквивалентная исходной системе сил.

Сложение сил построением параллелограммов можно заменить построением силового треугольника – выбирается одна из сил или изображается параллельно самой себе с началом в любой произвольной точке, все другие силы изображаются параллельными самим себе с началом, совпадающим с концом предыдущей силы .

Результатом такого сложения является вектор, направленный из начала первой силы к концу последней из сил .

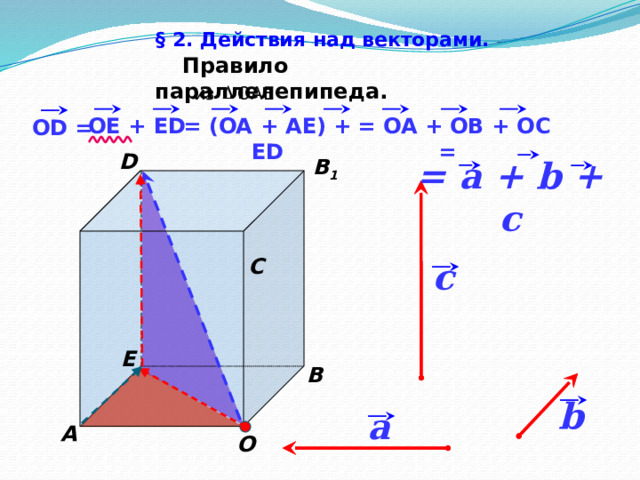
§ 2. Действия над векторами.

Правило параллелепипеда.

из OAE

= OA + OB + OC =

= (OA + AE) + ED

OE + ED

OD =

D

В 1

= a + b + c

С

c

«Геометрия 10-11» Л.С. Атанасян и др.

Е

В

b

a

A

О

14

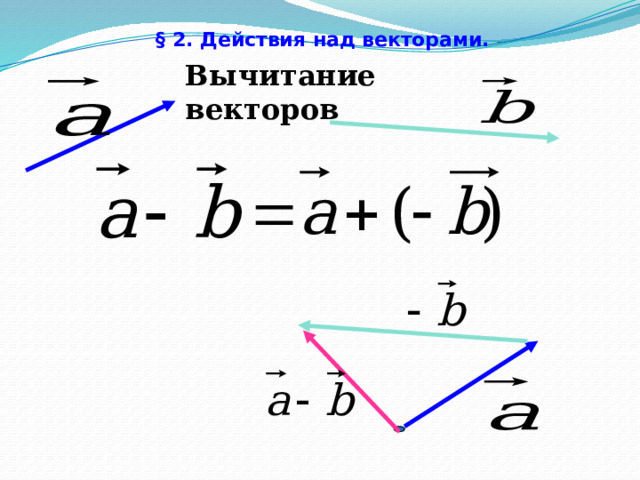
§ 2. Действия над векторами.

Вычитание векторов

15

§ 2. Действия над векторами.

Умножение вектора на число

Произведением вектора на число α называется вектор, такой что:

16

§ 2. Действия над векторами.

Умножение вектора на число

17

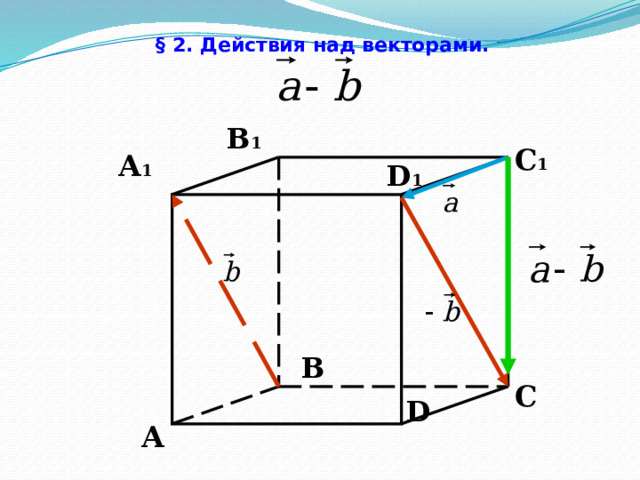
§ 2. Действия над векторами.

В 1

С 1

А 1

D 1

В

C

D

А

18

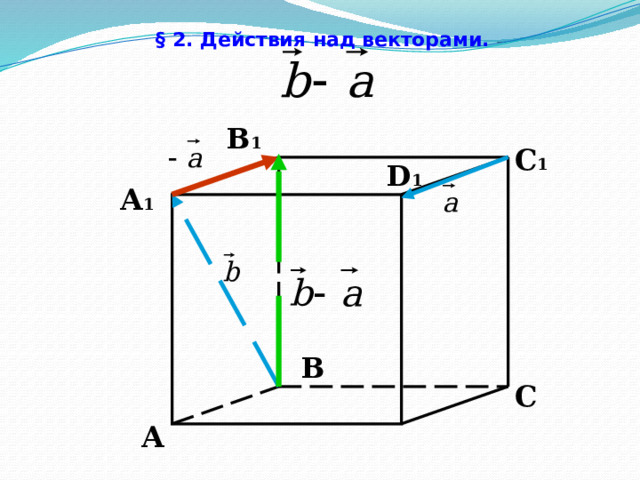
§ 2. Действия над векторами.

В 1

С 1

D 1

А 1

В

C

А

19

§ 3. Линейная зависимость векторов

Определение 1. Линейной комбинацией векторов

называется вектор

где λ i – некоторые числа.

Определение 2. Вектора называются линейно зависимыми ,

если существуют действительные числа λ i , такие, что хотя бы одно из них отлично от нуля, и при этом выполняется равенство:

Определение 2. Вектора называются линейно независимыми ,

если из условия

следует тривиальная комбинация

20

§ 3. Линейная зависимость векторов

Теорема 1. Для линейной зависимости векторов

необходимо и достаточно, чтобы один из них был линейной комбинацией остальных.

Доказательство.

Необходимость.

Пусть вектора линейно зависимы. Тогда существуют числа λ i , не равные нулю одновременно, такие, что

Пусть λ 1 ≠0, тогда

что доказывает необходимость.

Достаточность.

Пусть для определенности

Тогда

причем

Это и есть условие линейной зависимости.

21

§ 3. Линейная зависимость векторов

Для линейно зависимых векторов справедливы теоремы 2–6.

Теорема 2. Один вектор линейно зависим тогда и только тогда, когда он нулевой.

Теорема 3. Два вектора линейно зависимы тогда и только тогда, когда они коллинеарны.

Теорема 4. Три вектора линейно зависимы тогда и только тогда, когда они компланарны.

Доказательство.

Необходимость.

Пусть три вектора линейно зависимы. Тогда существуют не равные одновременно нулю три числа , такие, что

Тогда по теореме 1 один из векторов есть линейная комбинация двух остальных, и, значит, данные три вектора компланарны.

22

§ 3. Линейная зависимость векторов

Теорема 5. Любые четыре вектора в пространстве линейно зависимы.

Действительно, можно подобрать, причем единственным образом, такие числа

что будет

Теорема 6. Если среди векторов имеется хотя бы один нулевой вектор, то вектора линейно зависимы.

23

§ 3. Линейная зависимость векторов

Свойства линейно независимых векторов:

• Один вектор линейно независим тогда и только тогда, когда он ненулевой.
• Два вектора линейно независимы тогда и только тогда, когда они неколлинеарны.
• Три вектора линейно независимы тогда и только тогда, когда они некомпланарны.

24

§ 4. Базис. Координаты вектора в базисе.

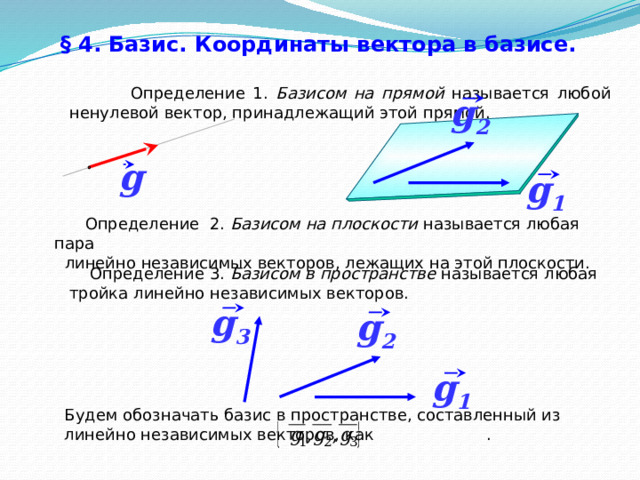
Определение 1. Базисом на прямой называется любой ненулевой вектор, принадлежащий этой прямой.

g 2

g

g 1

Определение 2. Базисом на плоскости называется любая пара

линейно независимых векторов, лежащих на этой плоскости.

Определение 3. Базисом в пространстве называется любая тройка линейно независимых векторов.

g 3

g 2

g 1

Будем обозначать базис в пространстве, составленный из линейно независимых векторов, как .

25

§ 4. Базис. Координаты вектора в базисе.

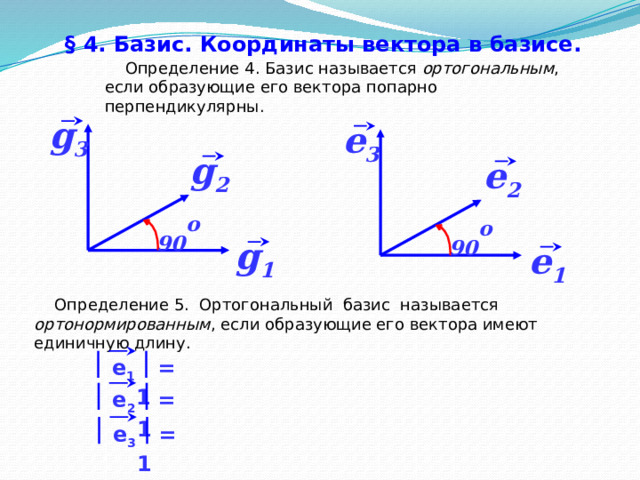
Определение 4. Базис называется ортогональным , если образующие его вектора попарно перпендикулярны.

g 3

e 3

g 2

e 2

90 o

90 o

g 1

e 1

Определение 5. Ортогональный базис называется ортонормированным , если образующие его вектора имеют единичную длину.

e 1 = 1

e 2 = 1

e 3 = 1

26

§ 4. Базис. Координаты вектора в базисе.

Теорема 1. Любой вектор в пространстве с базисом может быть представлен, и причем единственным способом, в виде

где α, β, γ – некоторые числа.

Докажем вначале, что такие числа существуют.

Доказательство.

и в силу коллинеарности

и в силу коллинеарности

Следовательно,

и

Докажем единственность разложения по данному базису.

Пусть

Но это условие и означает, что вектора являются линейно зависимыми и не могут образовывать базис. Это, в свою очередь, доказывает единственность разложения.

27

§ 4. Базис. Координаты вектора в базисе.

Определение 6. Числа в разложении называются координатами вектора в базисе .

Координаты – величины скалярные.

Для краткой записи вектора в координатном представлении будем использовать следующую форму: т. е. каждому вектору в данном базисе можно поставить во взаимно однозначное соответствие матрицу-строку.

28

§ 5. Действия с векторами в координатном представлении.

В каждом конкретном базисе каждый вектор находится во взаимно-однозначном соответствии с упорядоченной тройкой чисел – своими координатами. Возникает вопрос о том, как выполнять операции с векторами в координатном представлении.

С другой стороны, ранее были изучены матрицы и операции над ними, и целесообразно было бы свести операции с векторами в координатном представлении к матричным операциям.

Теорема 1. Два вектора

и

равны тогда и только тогда, когда равны матрицы координат

29

§ 5. Действия с векторами в координатном представлении.

Теорема 2. Пусть в некотором базисе даны два вектора

и

Тогда в этом базисе

Иными словами: при умножении вектора на число его координаты умножаются на это число; при сложении векторов складываются их соответствующие координаты .

30

§ 5. Действия с векторами в координатном представлении.

Теорема 3. Два вектора

и на плоскости линейно зависимы тогда и только тогда, когда их соответствующие координаты в некотором базисе пропорциональны, т. е.

Доказательство.

и

Пусть вектора

линейно зависимы, тогда по

Необходимость.

или в координатной форме

теореме 3.1

Исключив λ из этих уравнений, получаем

что и означает равенство нулю определителя.

Пусть

Достаточность.

Тогда

откуда

и

Таким образом, вектора

пропорциональны, а, значит, и линейно зависимы.

31

§ 5. Действия с векторами в координатном представлении.

Теорема 4. Три вектора в пространстве

и

линейно зависимы тогда и только тогда, когда

Следствие. Равенства

и

соответственно являются необходимыми и достаточными условиями коллинеарности пары векторов на плоскости и компланарности тройки векторов в пространстве.

32

§ 5. Действия с векторами в координатном представлении.

Пример 1. Показать, что вектора

образуют базис в трехмерном пространстве.

Решение.

Вычислим определитель, столбцы которого представляют координаты векторов:

Так как определитель отличен от нуля, то столбцы линейно независимы, т. е. указанные вектора образуют базис.

33

§ 5. Действия с векторами в координатном представлении.

Пример 2.

Разложить вектор

где

по базису

Решение.

с неопределенными

Разложим вектор

по базису

коэффициентами

В координатах это разложение представляет собой систему трех уравнений относительно

Имеем:

откуда по правилу Крамера

Ответ:

34

§ 6. Декартова система координат.

Определение 1.

Совокупность базиса

и точки О ,

в которую помещены начала всех базисных векторов, называется декартовой системой координат и обозначается

состоящая из

Определение 2. Система координат

ортонормированного ортогонального базиса и точки О , называется прямоугольной декартовой системой координат .

z

Ох – ось абсцисс

k

Оу – ось ординат

O

y

j

Оz – ось аппликат

i

x

35

§ 6. Декартова система координат.

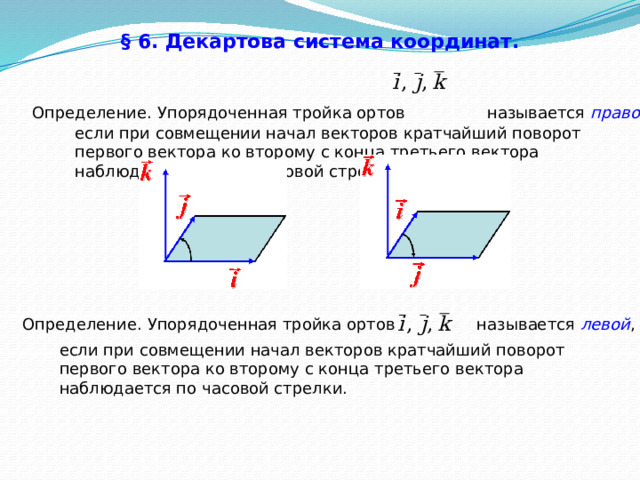
Определение. Упорядоченная тройка ортов называется правой ,

если при совмещении начал векторов кратчайший поворот первого вектора ко второму с конца третьего вектора наблюдается против часовой стрелки.

Определение. Упорядоченная тройка ортов называется левой ,

если при совмещении начал векторов кратчайший поворот первого вектора ко второму с конца третьего вектора наблюдается по часовой стрелки.

36

§ 6. Декартова система координат.

то произвольной точке

Если задана система координат

М в пространстве можно поставить во взаимно однозначное соответствие вектор

начало которого находится в точке О ,

а конец в точке М .

называется радиус-вектором

Определение 3. Вектор

точки М в системе координат

Определение 4. Координаты радиус-вектора точки М называются координатами точки М в системе координат

37

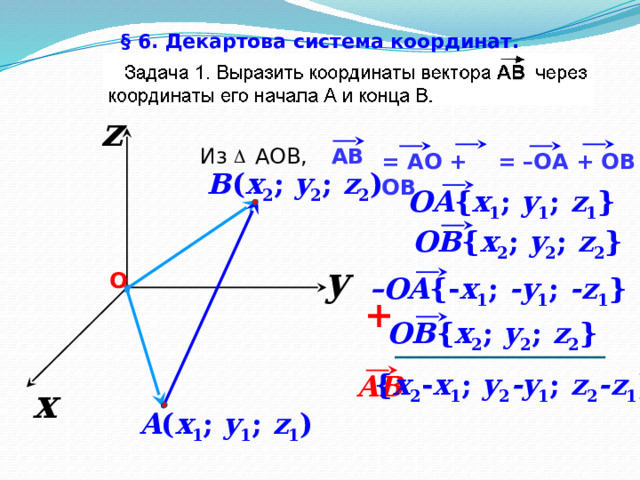
§ 6. Декартова система координат.

z

Из АОB,

AB

= –ОA + ОB

= AО + ОB

B ( x 2 ; y 2 ; z 2 )

OA { x 1 ; y 1 ; z 1 }

OB { x 2 ; y 2 ; z 2 }

y

О

– OA {- x 1 ; -y 1 ; -z 1 }

+

OB { x 2 ; y 2 ; z 2 }

{ x 2 - x 1 ; y 2 -y 1 ; z 2 -z 1 }

AB

x

A ( x 1 ; y 1 ; z 1 )

38

§ 7. Проекция вектора на ось.

Пусть вектор лежит на некоторой оси l . Направление орта соответствует направлению оси.

l

Определение 1. Проекцией вектора , лежащего на оси, на эту ось называется число, по абсолютной величине равное длине вектора и взятое со знаком плюс, если направление вектора совпадает с направлением оси и со знаком минус, если они противоположны.

Пусть вектор не лежит на некоторой оси l . Из точек А и B опустим перпендикуляры на ось. Вектор называется компонентой вектора по оси l .

Определение 2. Проекцией вектора, не лежащего на оси l , на эту ось называется проекция его компоненты по оси l на эту же ось.

Проекция вектора на ось обычно обозначается так:

39

§ 7. Проекция вектора на ось.

Свойства проекций вектора на ось:

1. Проекция вектора на ось равна произведению длины вектора на косинус угла между вектором и осью:

где θ – угол между вектором и осью.

2. Проекция суммы векторов на ось равна сумме проекций этих векторов на эту же ось, т. е.

.

3. Проекция на ось вектора, умноженного на число, равна произведению проекции вектора на это число, т. е.

4. Проекции на ось двух равных векторов равны между собой.

40

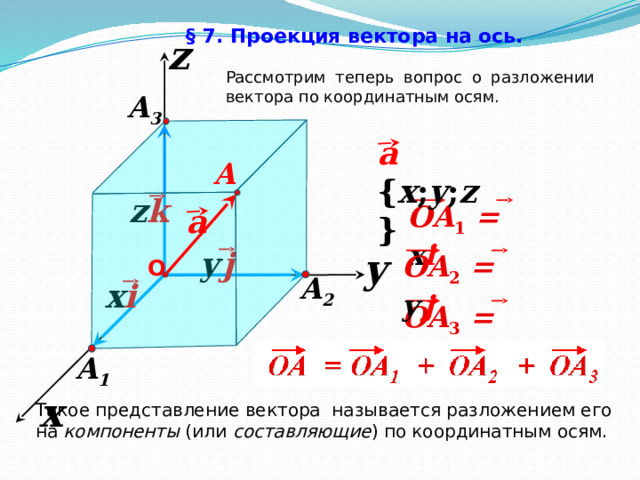
§ 7. Проекция вектора на ось.

z

Рассмотрим теперь вопрос о разложении вектора по координатным осям.

A 3

a { x ; y ; z }

A

z k

OA 1 = x i

a

y

y j

OA 2 = y j

О

A 2

x i

OA 3 = z k

A 1

x

Такое представление вектора называется разложением его на компоненты (или составляющие ) по координатным осям.

41

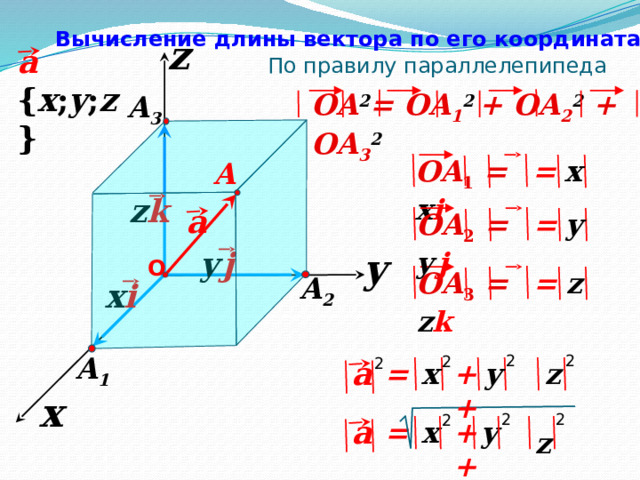
Вычисление длины вектора по его координатам

z

a { x ; y ; z }

По правилу параллелепипеда

OA 2 = OA 1 2 + OA 2 2 + OA 3 2

A 3

x

=

OA 1 = x i

A

z k

a

OA 2 = y j

=

y

y j

y

О

z

OA 3 = z k

=

A 2

x i

A 1

2

2

2

a

2

+ +

z

x

y

=

x

2

2

2

a

z

y

x

=

+ +

42

§ 8. Скалярное произведение векторов.

Скалярным произведением двух ненулевых векторов называется произведение их длин на косинус угла между ними.

a

b

a

a

b

b

cos ( )

=

Если хотя бы один из векторов равен нулю, то скалярное произведение этих векторов равно нулю (по определению).

Скалярное произведение векторов – число (скаляр). Скаляр – лат. scale – лестница, шкала.

Ввел в 1845г. У. Гамильтон, ирландский математик.

43

§ 8. Скалярное произведение векторов.

0

b

a

= 90 0

a

a

b

b

cos 90 0

=

= 0

b

a

b

a

Если векторы и перпендикулярны, то скалярное произведение векторов равно нулю.

b

a

b

a

= 0

Обратно: если , то векторы и перпендикулярны.

Скалярное произведение ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны.

b

a

a

b

Û

= 0

^

44

0 b a a b cos b 0 a = a Скалярное произведение ненулевых векторов положительно тогда и только тогда , когда угол между векторами острый. b a Û a b 90 0 0 45 " width="640"

§ 8. Скалярное произведение векторов.

b

a

90 0

0

b

a

a

b

cos

b

0

a

=

a

Скалярное произведение ненулевых векторов положительно тогда и только тогда , когда угол между векторами острый.

b

a

Û

a

b

90 0

0

45

90 0 a a b b cos a 0 b = a Скалярное произведение ненулевых векторов отрицательно тогда и только тогда , когда угол между векторами тупой. b a Û b a 90 0 0 46 " width="640"

§ 8. Скалярное произведение векторов.

a

b

90 0

a

a

b

b

cos

a

0

b

=

a

Скалярное произведение ненулевых векторов отрицательно тогда и только тогда , когда угол между векторами тупой.

b

a

Û

b

a

90 0

0

46

§ 8. Скалярное произведение векторов.

a

a

= 0 0

a

a 2

a

a

a

a

a

cos

a

0 0

=

=

=

a

a

Скалярное произведение называется

скалярным квадратом вектора и обозначается

a

a 2

a 2

a 2

Таким образом,

откуда

=

Длина вектора равен квадратному корню из его скалярного квадрата.

47

§ 8. Скалярное произведение векторов.

Свойства скалярного произведения:

тогда

Действительно,

Отсюда следует формула для нахождения проекции одного вектора на другой:

2) Переместительное или коммутативное свойство:

3) Сочетательное (ассоциативное) свойство:

4) Распределительное (дистрибутивное) свойство относительного сложения векторов:

48

§ 8. Скалярное произведение векторов.

Выведем формулу скалярного произведения в координатной форме.

a {а x ;а y ;а z }

b {b x ;b y ;b z }

т.к.

.

В частности,

49

§ 8. Скалярное произведение векторов.

Скалярное произведение векторов встречается в физике. Например, из курса механики известно, что работа A постоянной силы F при перемещении тела из точки M в

F

j

N

M

точку N равна произведению силы F и перемещения MN на косинус угла между ними.

A = F MN cos

j

A = F MN

50

§ 8. Скалярное произведение векторов.

Скалярное произведение двух векторов позволяет решить следующие задачи векторной алгебры:

• Нахождение угла между двумя векторами.

Отсюда нетрудно получить условие ортогональности (перпендикулярности) двух векторов в координатной форме:

51

§ 9. Векторное произведение векторов.

Введем еще одну операцию над векторами. Эта операция существует только в трехмерном векторном пространстве, на плоскости она не определена.

Векторным произведением двух ненулевых векторов называется вектор ,

удовлетворяющий трем требованиям:

a

b

sin ( )

a

b

b |

| a

1)

=

2)

3) Тройка векторов

является правой.

52

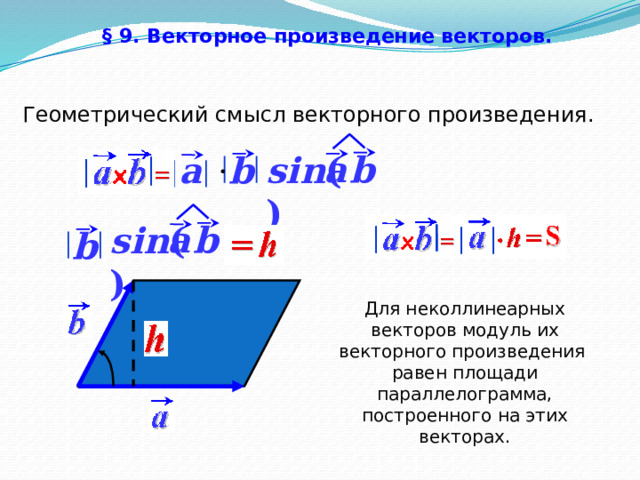
§ 9. Векторное произведение векторов.

Геометрический смысл векторного произведения.

b

a

sin ( )

a

b

b

a

sin ( )

b

Для неколлинеарных векторов модуль их векторного произведения равен площади параллелограмма, построенного на этих векторах.

53

§ 9. Векторное произведение векторов.

Свойства векторного произведения:

Свойство очевидно, так как синус – функция нечетная.

2 ) Свойство сочетательности относительно скалярного множителя:

3 ) Распределительное свойство относительно сложения векторов:

54

§ 8. Векторное произведение векторов.

Если вектора коллинеарные, то

b

a

= 0 0

b

a

a

b

sin

0 0

Признак коллинеарности векторов:

Для того чтобы два ненулевых вектора были коллинеарны, необходимо и достаточно, чтобы их векторное произведение было бы равно нулю.

В частности, имеем для ортов:

55

§ 9. Векторное произведение векторов.

Выразим теперь векторное произведение через координаты векторов, его составляющих.

56

§ 9. Векторное произведение векторов.

Векторное произведение двух векторов позволяет решить следующие задачи векторной алгебры.

1) Нахождение площади параллелограмма и треугольника

57

§ 10. Смешанное произведение векторов.

Определение 1.

Смешанным произведением ненулевых векторов

называется скалярное произведение вектора и векторного произведения вектора на вектор , т. е. выражение

Свойства смешанного произведения:

1) Смешанное произведение не меняется при циклической перестановке

перемножаемых векторов.

2) При перестановке двух соседних векторов модуль смешанного произведения не меняется, а знак меняется на противоположный, т. к. тройка меняет свою ориентацию.

т.е. порядок знаков умножения не важен.

Поэтому принято смешанное произведение обозначать

58

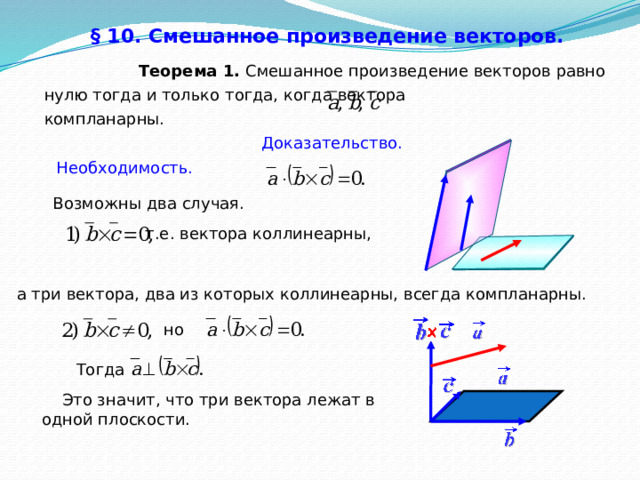
§ 10. Смешанное произведение векторов.

Теорема 1. Смешанное произведение векторов равно нулю тогда и только тогда, когда вектора компланарны.

Доказательство.

Необходимость.

Возможны два случая.

т.е. вектора коллинеарны,

а три вектора, два из которых коллинеарны, всегда компланарны.

но

Тогда

Это значит, что три вектора лежат в

одной плоскости.

59

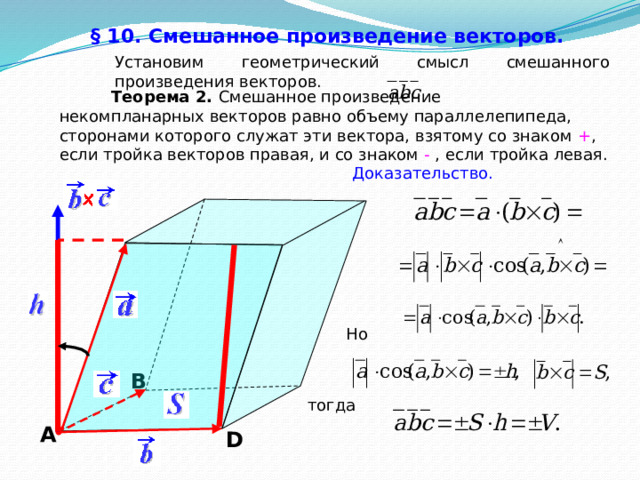
§ 10. Смешанное произведение векторов.

Установим геометрический смысл смешанного произведения векторов.

Теорема 2. Смешанное произведение некомпланарных векторов равно объему параллелепипеда, сторонами которого служат эти вектора, взятому со знаком + , если тройка векторов правая, и со знаком - , если тройка левая.

Доказательство.

Но

В

тогда

А

D

60