Презентация "Объем пирамиды" 11 класс

Тема урока:

Объем пирамиды.

Что мы знаем о пирамиде?

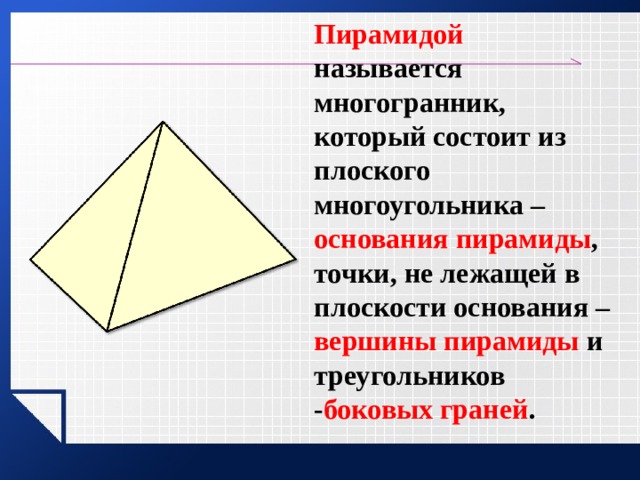
Пирамидой называется многогранник, который состоит из плоского многоугольника – основания пирамиды , точки, не лежащей в плоскости основания – вершины пирамиды и треугольников - боковых граней .

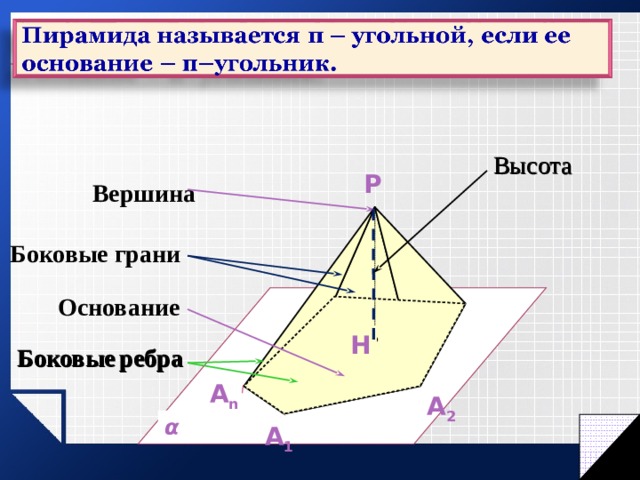
Высота

P

Вершина

Боковые грани

Основание

H

Боковые ребра

А n

А 2

α

А 1

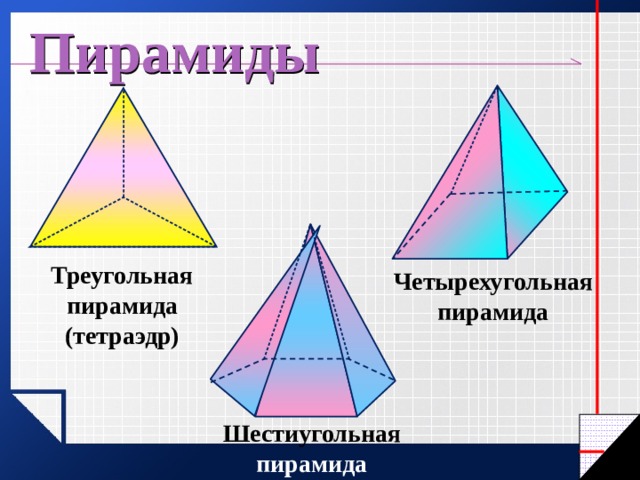
Пирамиды

Треугольная пирамида (тетраэдр)

Четырехугольная пирамида

Шестиугольная пирамида

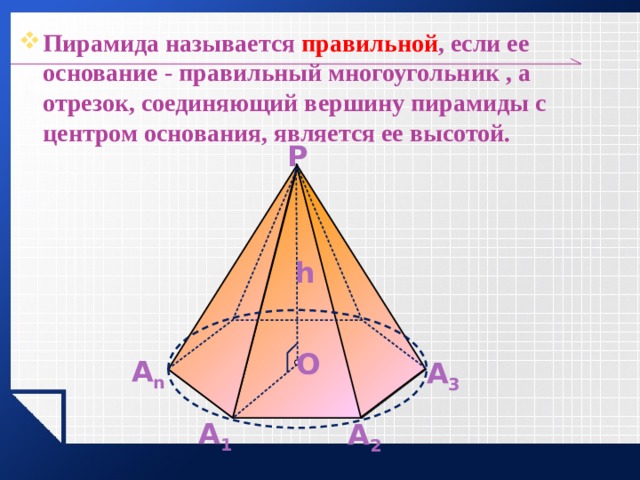
• Пирамида называется правильной , если ее основание - правильный многоугольник , а отрезок, соединяющий вершину пирамиды с центром основания, является ее высотой.

P

h

O

А n

А 3

А 1

А 2

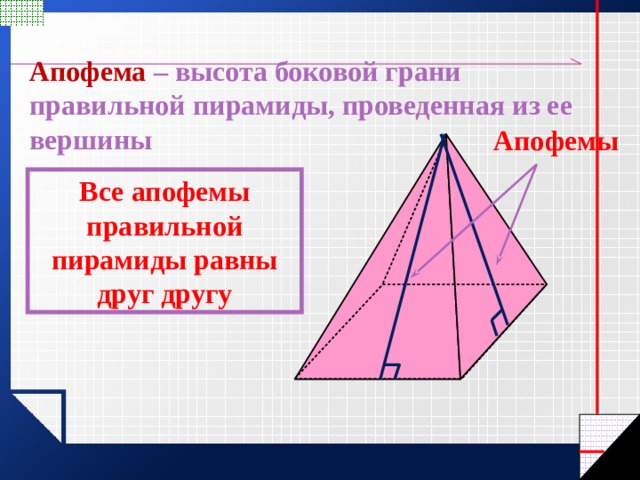
Апофема – высота боковой грани правильной пирамиды, проведенная из ее вершины

Апофемы

Все апофемы правильной пирамиды равны друг другу

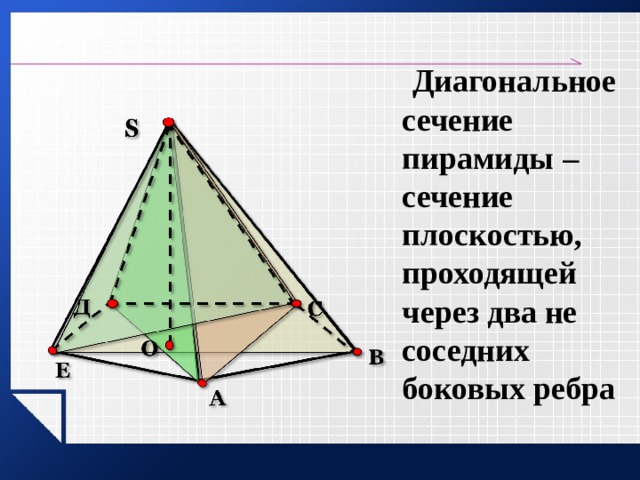
Диагональное сечение пирамиды – сечение плоскостью, проходящей через два не соседних боковых ребра

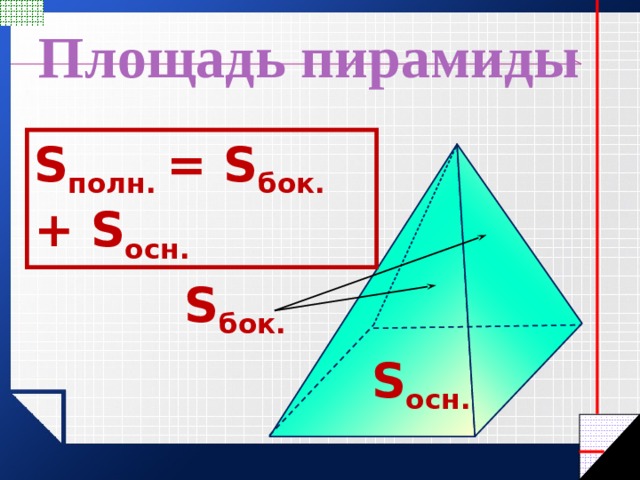
Площадь пирамиды

S полн. = S бок. + S осн.

S бок.

S осн.

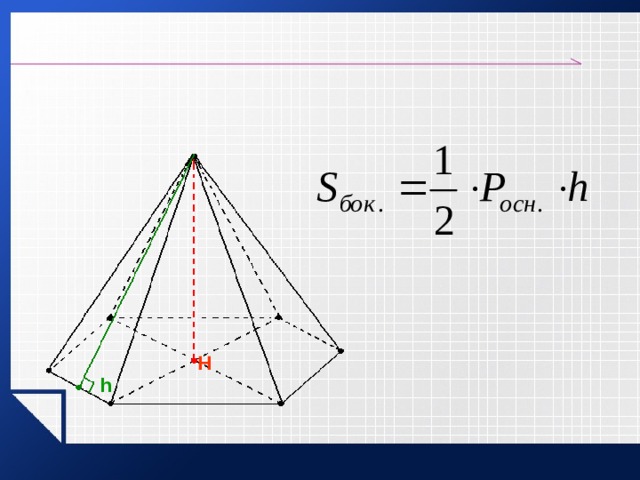
H

h

Свойства пирамиды:

У правильной пирамиды:

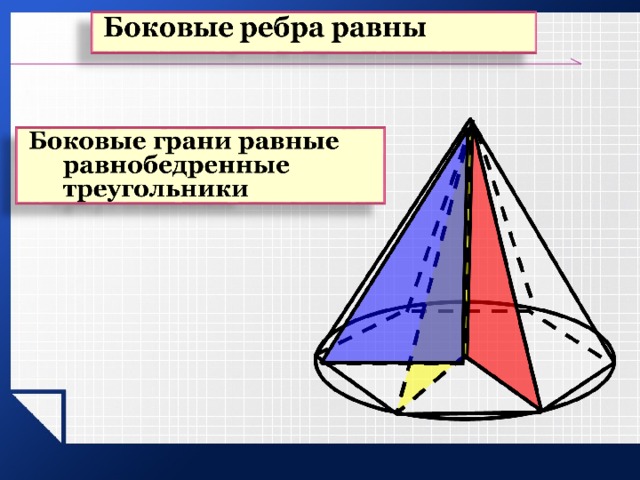
• боковые ребра равны;
• боковые грани являются равными равнобедренными треугольниками;
• апофемы равны;
• площадь боковой поверхности правильной пирамиды равна половине произведения периметра на апофему.

Свойства пирамиды:

• если боковые ребра пирамиды равны (или составляют равные углы с плоскостью основания), то вершина пирамиды проецируется в центр окружности, описанной около основания.

• если двугранные углы при основании пирамиды равны (или равны высоты боковых граней, проведенные из вершины пирамиды), то вершина пирамиды проецируется в центр окружности, вписанной в основание пирамиды.

Теорема: Объём пирамиды равен одной трети произведения площади основания на высоту.

∙

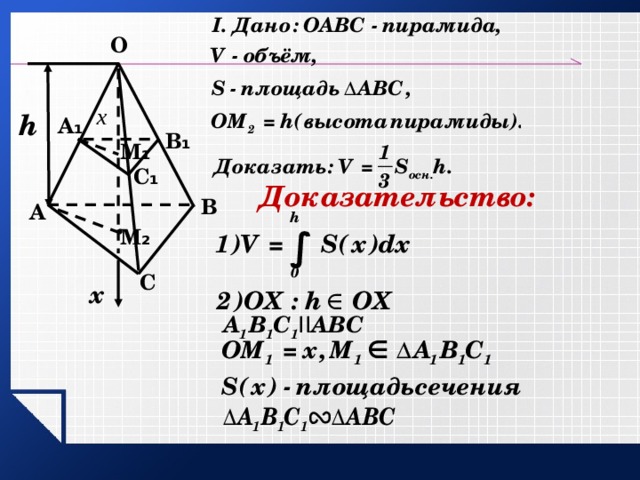
O

h

А ₁

В ₁

М ₁

С ₁

Доказательство:

В

А

М ₂

С

х

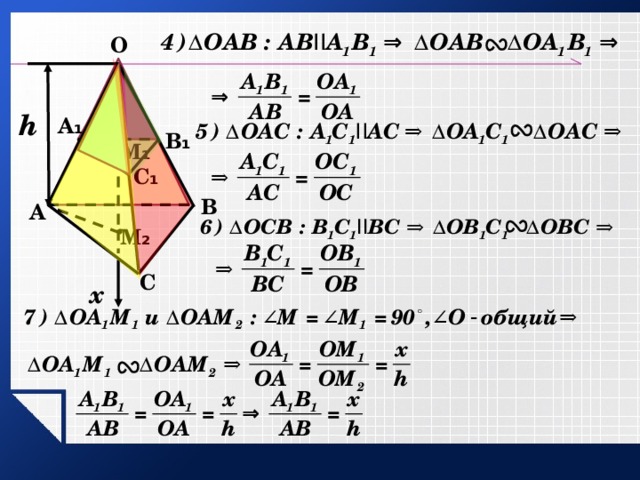
O

h

А ₁

В ₁

М ₁

С ₁

В

А

М ₂

С

х

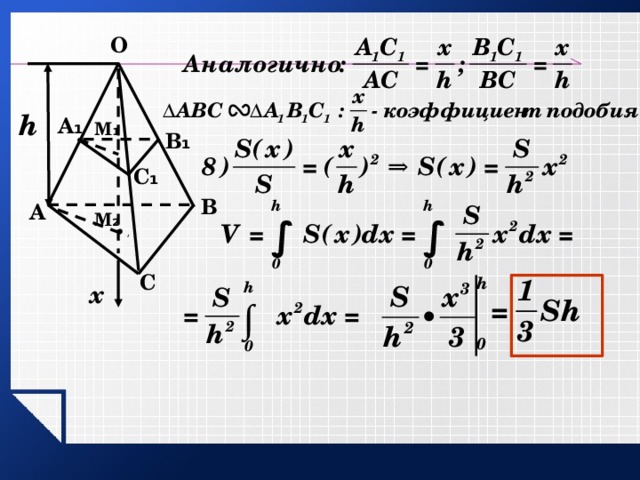
O

h

А ₁

М ₁

В ₁

С ₁

В

А

М ₂

С

х

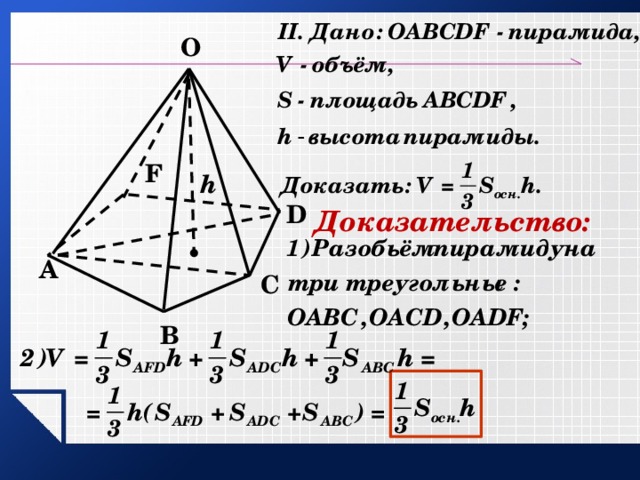
О

F

h

D

Доказательство:

А

С

В

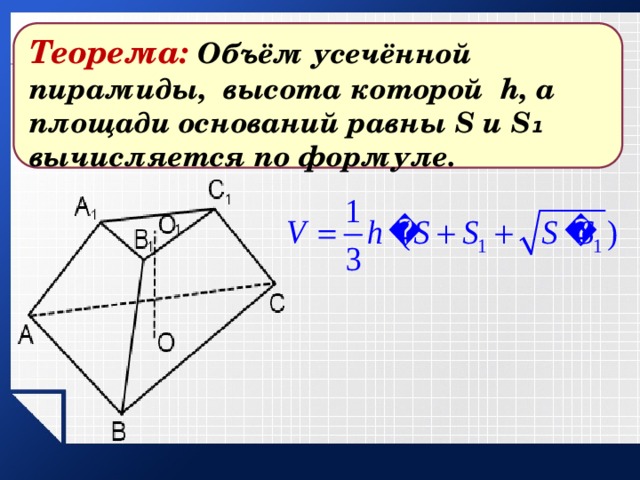
Теорема: Объём усечённой пирамиды, высота которой h, а площади оснований равны S и S₁ вычисляется по формуле.

• Объем усеченной пирамиды будем рассматривать как разность объемов полной пирамиды и той, что отсечена от нее плоскостью, параллельной основанию

Объем полной пирамиды

(1)

Подставляем в уравнение 1

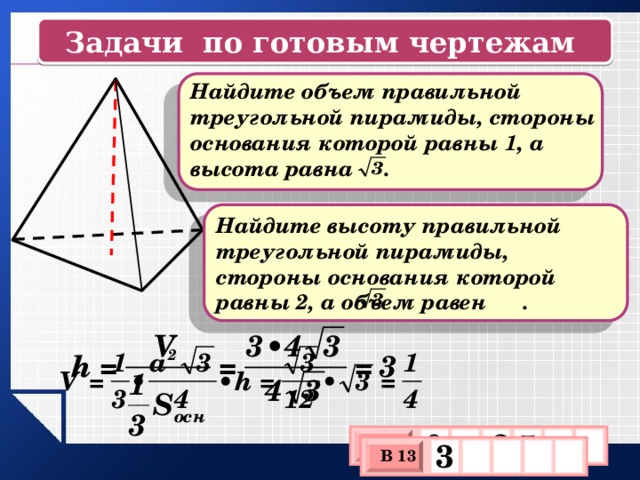
Задачи по готовым чертежам

Найдите объем правильной треугольной пирамиды, стороны основания которой равны 1, а высота равна .

Найдите высоту правильной треугольной пирамиды, стороны основания которой равны 2, а объем равен .

0

2

,

5

В 13

3

х

3

х

1

0

В 13

х

3

х

1

0

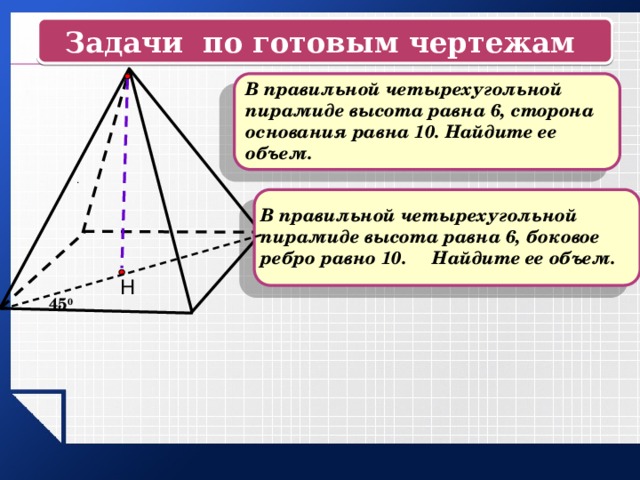
Задачи по готовым чертежам

В правильной четырехугольной пирамиде высота равна 6, сторона основания равна 10. Найдите ее объем.

.

В правильной четырехугольной пирамиде высота равна 6, боковое ребро равно 10. Найдите ее объем.

Н

45 0

Задачи (база)

Сторона основания правильной треугольной пирамиды равна 6, а боковое ребро образует с плоскостью основания угол 45 0 . Найдите объем пирамиды.

Высота правильной треугольной пирамиды равна , а боковая грань образует с плоскостью основания угол 60 0 . Найдите объем пирамиды.

Задачи (профиль)

Объем треугольной пирамиды SABC, являющейся частью правильной шестиугольной пирамиды SABCDEF, равен 8. Найдите объем шестиугольной пирамиды.

От треугольной пирамиды, объем которой равен 12, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания.

Найдите объем отсеченной треугольной пирамиды.

Домашнее

задание:

П. 80, № 685,

686.