Презентация "Осевая и центральная симметрия"

Осевая и центральная симметрия

Презентация урока геометрии в 8 классе

Содержание

• Симметричность точек относительно прямой
• Симметричность фигуры относительно прямой
• Симметричность точек относительно точки
• Симметричность фигуры относительно точки
• Симметрия на координатной плоскости
• Симметрия вокруг нас
• Математики о симметрии
• Проверим знания
• Задания

Т

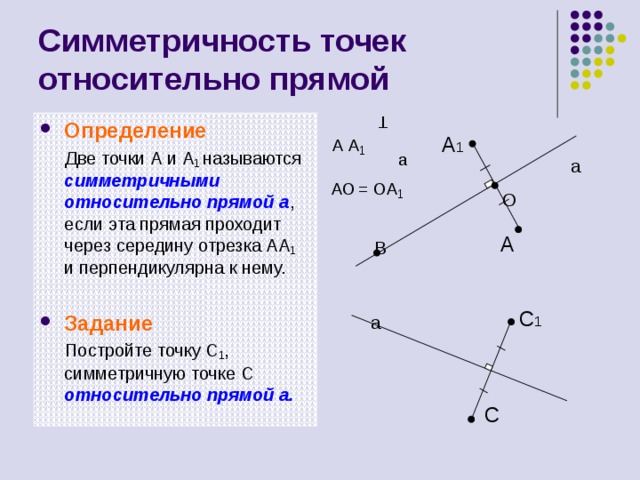
Симметричность точек относительно прямой

a

A A 1

• Определение

Две точки А и А 1 называются симметричными относительно прямой а , если эта прямая проходит через середину отрезка АА 1 и перпендикулярна к нему.

• Задание

Постройте точку C 1 , симметричную точке C относительно прямой а.

A 1

a

AO = OA 1

O

B

A

a

C 1

C

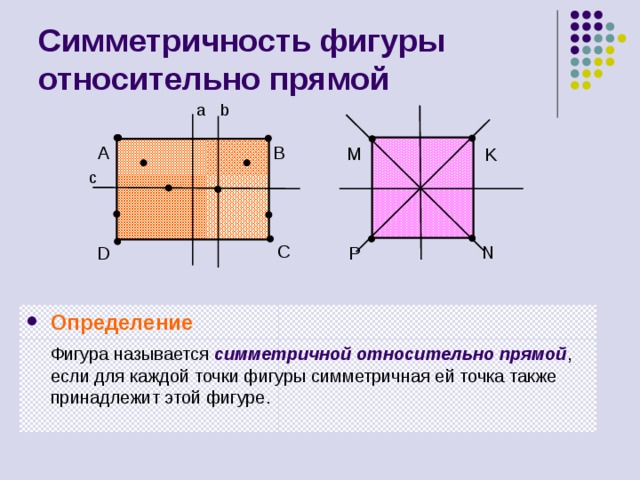
Симметричность фигуры относительно прямой

a

b

А

B

M

K

c

C

N

P

D

• Определение

Фигура называется симметричной относительно прямой , если для каждой точки фигуры симметричная ей точка также принадлежит этой фигуре.

Подумай!

• Какие из данных фигур имеют ось симметрии? Сколько?

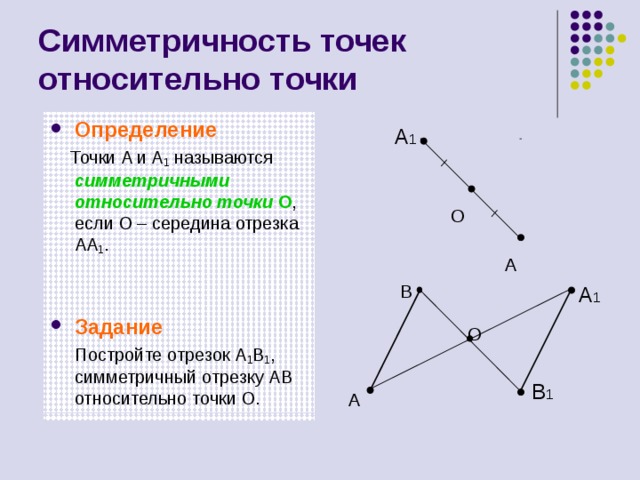
Симметричность точек относительно точки

• Определение

Точки A и A 1 называются симметричными относительно точки О , если О – середина отрезка AA 1 .

• Задание

Постройте отрезок A 1 B 1 , симметричный отрезку AB относительно точки О.

A 1

O

A

B

A 1

O

A

B 1

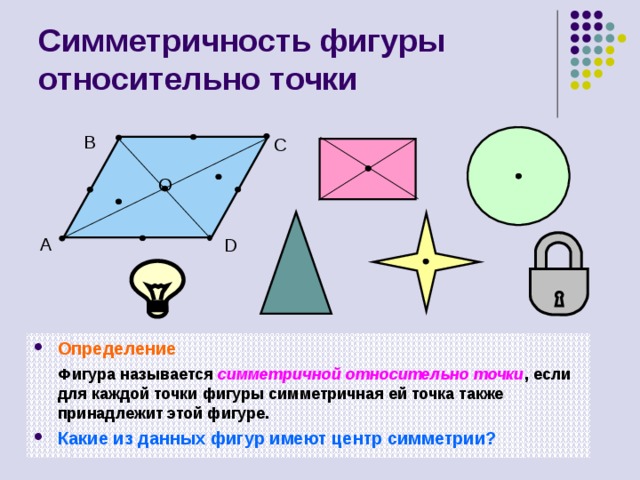
Симметричность фигуры относительно точки

B

C

O

A

D

• Определение

Фигура называется симметричной относительно точки , если для каждой точки фигуры симметричная ей точка также принадлежит этой фигуре.

• Какие из данных фигур имеют центр симметрии?

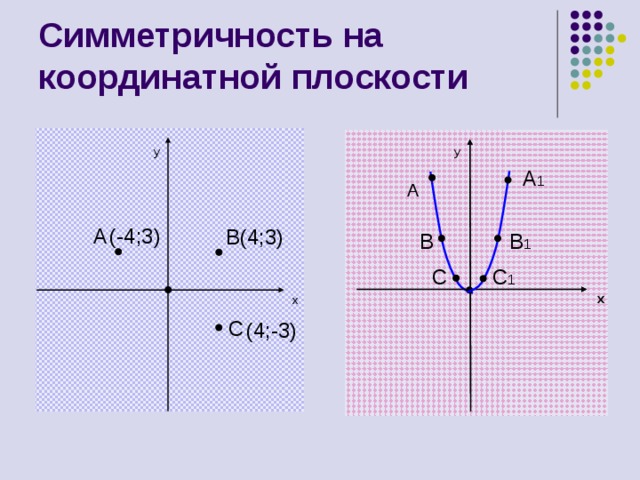
Симметричность на координатной плоскости

y

y

A

A 1

(-4;3)

A

B (4;3)

B 1

B

C

C 1

x

x

C

(4;-3)

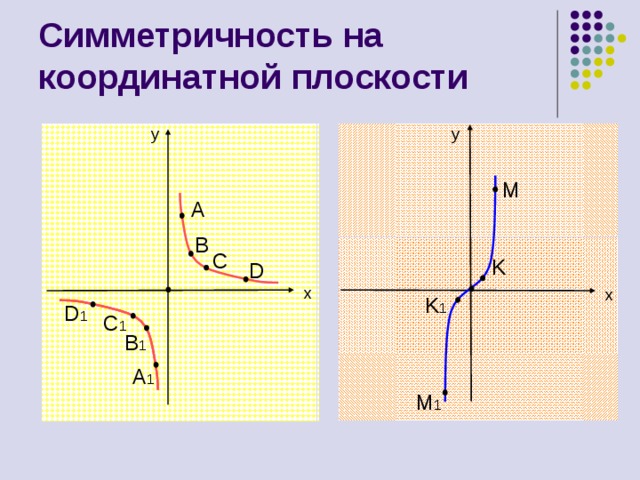
Симметричность на координатной плоскости

y

y

M

A

B

C

K

D

x

x

K 1

D 1

C 1

B 1

A 1

M 1

Симметрия вокруг нас

• С симметрией мы часто встречаемся в природе

Симметрия вокруг нас

Многие предметы

окружающего нас мира имеют

ось симметрии

или

центр симметрии

Математики о симметрии

• Математик любит прежде всего симметрию

Максвелл Д.

• Красота тесно связана с симметрией

Вейль Г.

• Симметрия … является той идеей, посредством которой человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство

Вейль Г .

• Для человеческого разума симметрия обладает, по - видимому, совершенно особой притягательной силой

Фейнман Р.

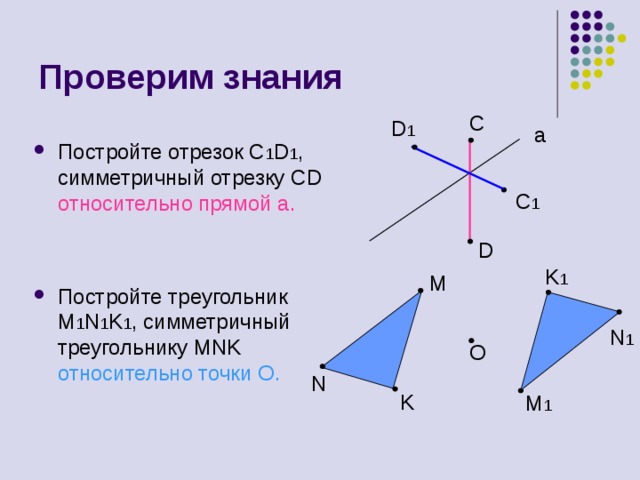
Проверим знания

С

D 1

a

• Постройте отрезок С 1 D 1 , симметричный отрезку С D относительно прямой а.

• Постройте треугольник M 1 N 1 K 1 , симметричный треугольнику MNK относительно точки O .

C 1

D

K 1

M

N 1

O

N

K

M 1

Задания

• Сколько осей симметрии имеет отрезок, прямая, луч?

• Какие из данных букв имеют ось симметрии?

• Имеют ли центр симметрии отрезок, прямая, квадрат?

• Какие из данных букв имеют центр симметрии?

Симметрию можно обнаружить почти везде, если знать, как ее искать. Многие народы с древнейших времен владели представлением о симметрии в широком смысле – как об уравновешенности и гармонии. Творчество людей во всех своих проявлениях тяготеет к симметрии. Посредством симметрии человек всегда пытался, по словам немецкого математика Германа Вейля, «постичь и создать порядок, красоту и совершенство».