Презентация "Параллелепипед и куб. Диагонали параллелепипеда и куба"

.

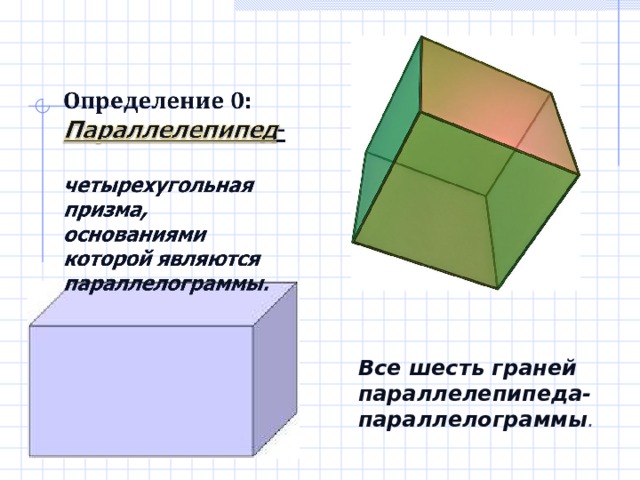
Все шесть граней параллелепипеда- параллелограммы .

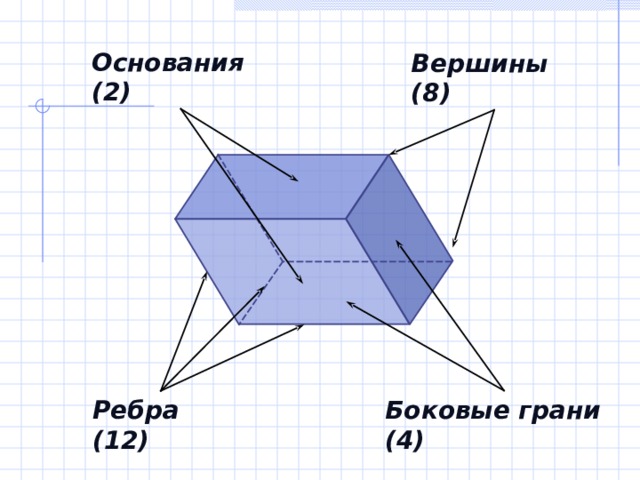
Основания (2)

Вершины (8)

Боковые грани (4)

Ребра (12)

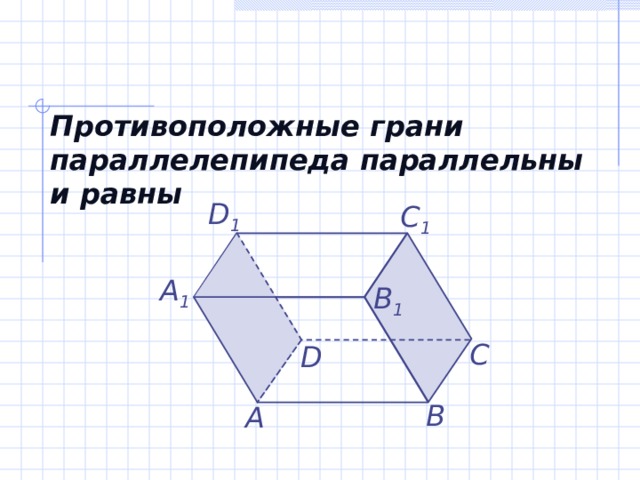
Противоположные грани параллелепипеда параллельны и равны

D 1

C 1

А 1

B 1

С

D

В

А

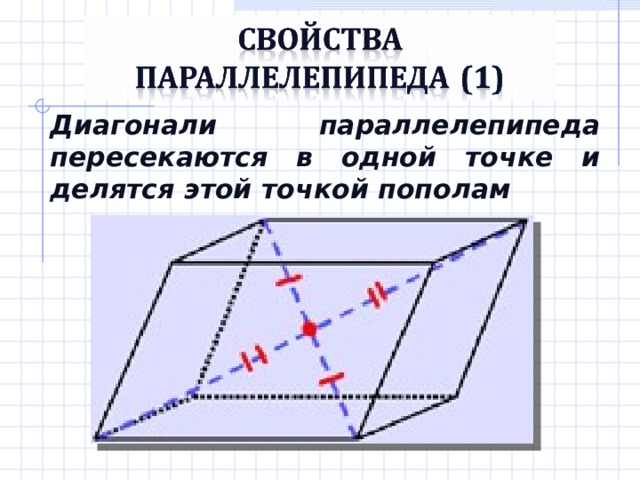
Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам

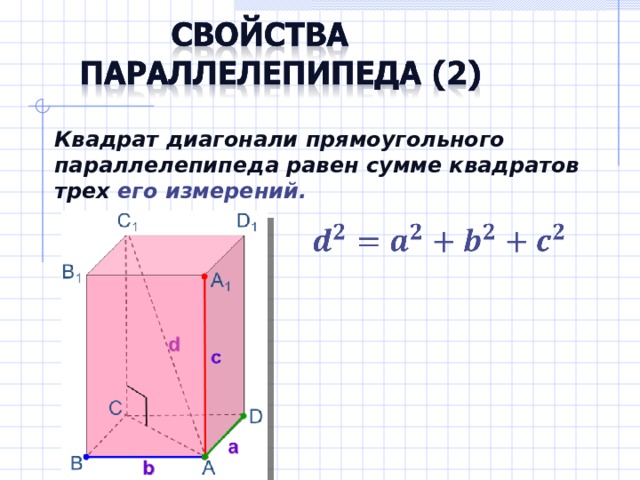
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.

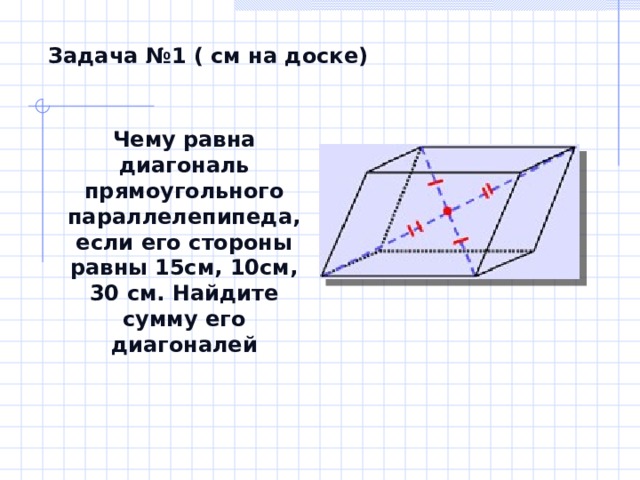
Задача №1 ( см на доске)

Чему равна диагональ прямоугольного параллелепипеда, если его стороны равны 15см, 10см, 30 см. Найдите сумму его диагоналей

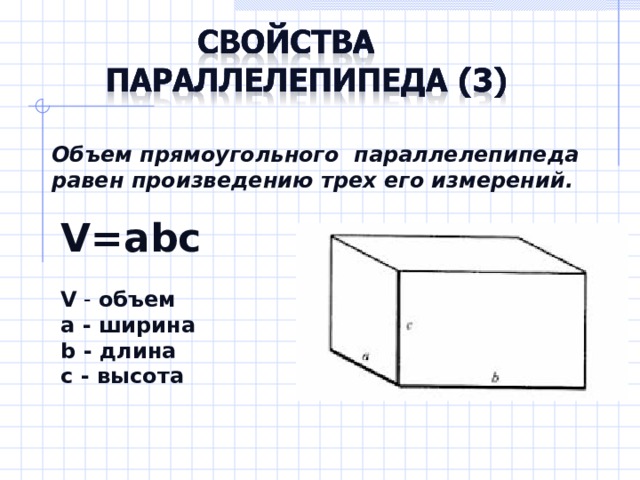
Объем прямоугольного параллелепипеда равен произведению трех его измерений.

V=abc

V - объем

a - ширина

b - длина

c - высота

Задача № 2 ( см на доске)

Найдите объем прямоугольного параллелепипеда, если его измерения равны 1дм, 5 см и 10 мм

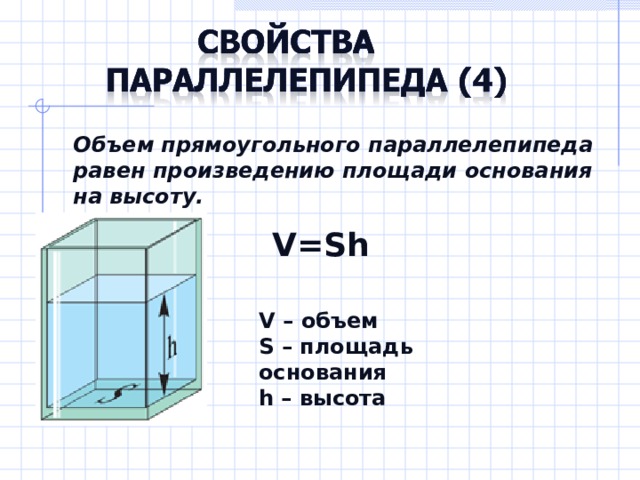
Объем прямоугольного параллелепипеда равен произведению площади основания на высоту.

V=Sh

V – объем

S – площадь основания

h – высота

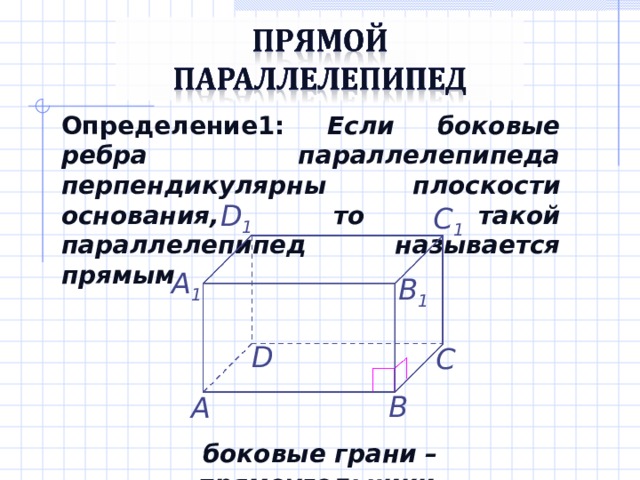
Определение1: Если боковые ребра параллелепипеда перпендикулярны плоскости основания, то такой параллелепипед называется прямым

D 1

C 1

А 1

B 1

D

С

В

А

боковые грани – прямоугольники

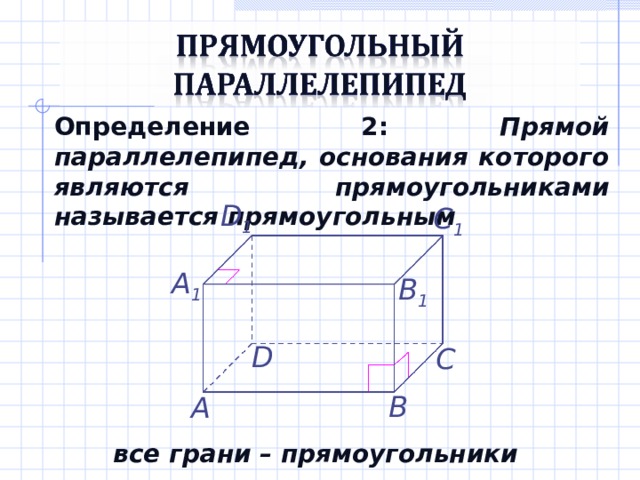
Определение 2: Прямой параллелепипед, основания которого являются прямоугольниками называется прямоугольным

D 1

C 1

А 1

B 1

D

С

В

А

все грани – прямоугольники

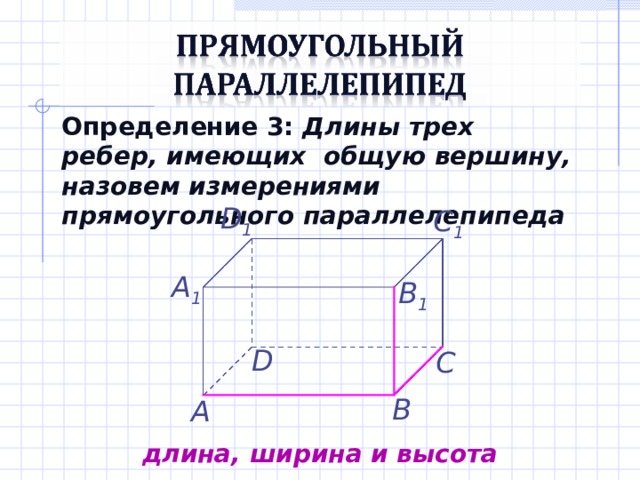
Определение 3: Длины трех ребер, имеющих общую вершину, назовем измерениями прямоугольного параллелепипеда

D 1

C 1

А 1

B 1

D

С

В

А

длина, ширина и высота

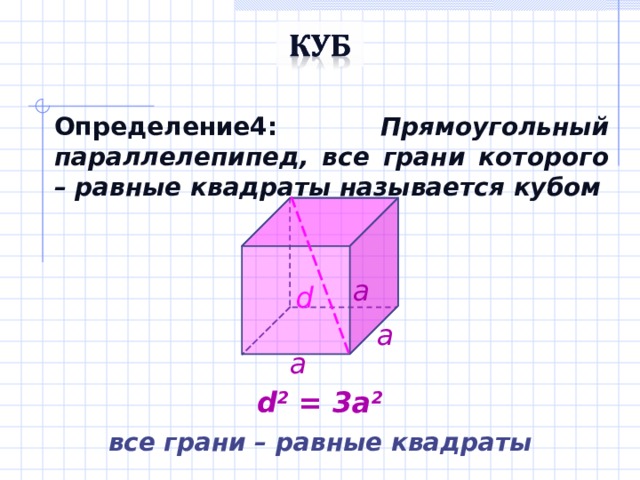
Определение4: Прямоугольный параллелепипед, все грани которого – равные квадраты называется кубом

a

d

a

a

d 2 = 3 a 2

все грани – равные квадраты

Задача № 3 ( см на доске)

Чему равна диагональ куба, если его сторона равна 10/√3 см?

Практическая работа № 2

Вычисление диагонали куба и параллелепипеда и их объемов

1. Начертите полученные фигуры

2. Измерьте длину, ширину и высоту параллелепипеда и куба

3. Вычислите длину диагонали данных фигур.

4.Сколько диагоналей у параллелепипеда? Начертите их. Найдите их сумму

5 . Найдите объем полученных фигур.

6. Сделайте вывод.

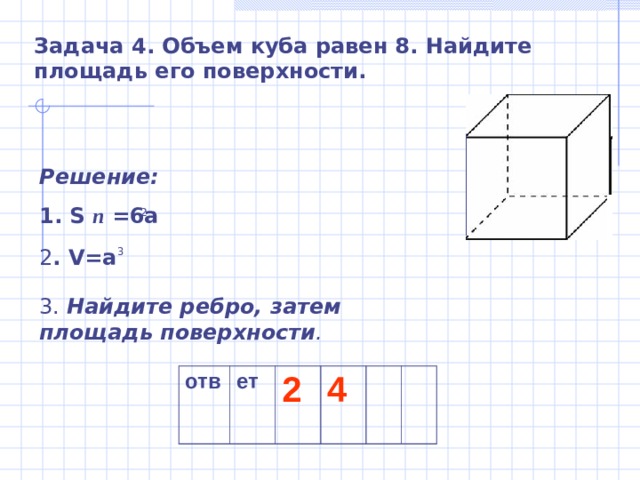
Задача 4. Объем куба равен 8. Найдите площадь его поверхности.

Решение:

1. S п =6а

2

2 . V =а

3

3. Найдите ребро, затем площадь поверхности .

отв

ет

2

4

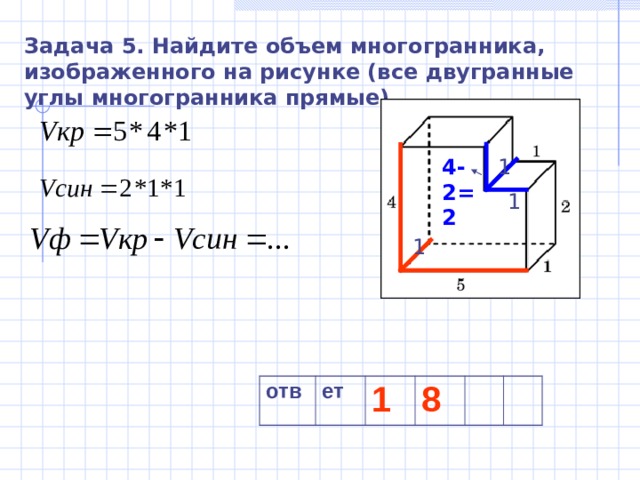
Задача 5. Найдите объем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые).

1

4-2=2

1

1

отв

ет

1

8