
Задачи с параметром
Графический метод решения задач с параметром на ОГЭ ( типовые задачи №22 КИМ ОГЭ)
Подготовила:
учитель математики
МОУ «Гимназия №1»
г. Железногорска Курской области
Агашкова Н.А.

Задача№1. Найдите все значенияk, при которых прямая y=kx пересекает в трех различных точках график функции:
f(x) =
Решение.
Построим график функции f(x) =
- y=kx– уравнение прямой, проходящей через начало координат
x
y
-3
-5
-2
-8
x
y
3
5
-2
4
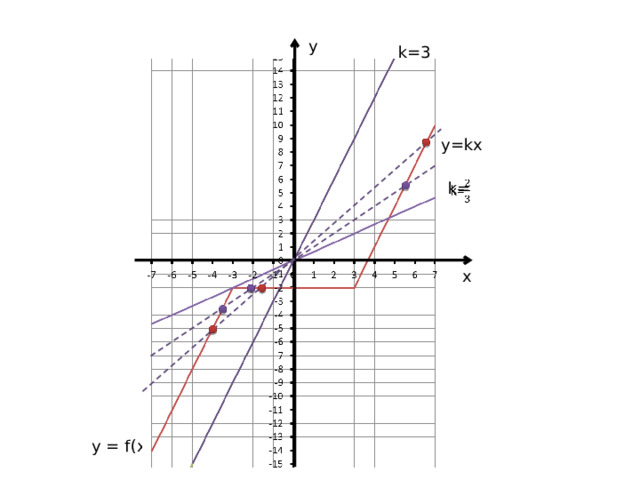
y
k=3
y=kx
k=
x
y = f(x)

5) Прямая y=kxпересекает в трех различных точках этот график, если её угловой коэффициент больше углового коэффициента прямой, проходящей через точку (-3 -2) и меньше углового коэффициента прямой, параллельной прямой y=3x+7 и y=3x-11
6) Найден угловой коэффициент прямой y=kx, проходящей через
точку (-3 -2):
-3k = -2 k =
7) Угловой коэффициент k прямой, параллельной прямой y=3x+7, равен 3.
Прямая y=kx имеет с графиком заданной функции три общие точки при
Ответ:

Задание для самостоятельного решения
Найдите все значенияпараметра k, при каждом из которых прямая y=kx пересекает в трех различных точках ломаную, заданную условиями:
a) y =
Ответ: k (1;2)
b)
Ответ: k (;2)
![Задача№2. При каких значениях p прямая y = p имеет три общие точки с графиком функции y = f(x), где f(x) = Решение. Построим график функции f(x) = 1) y = x(x - 4) = x²- 4x = (x²- 4x +4) – 4 = (x – 2)² - 4 y = (x – 2)² - 4 , x 0 (2; -4) - вершина параболы х = 2 – ось симметрии параболы 2) y = x(4 – x) = -x² +4x = -(x² - 4x) = -[(x² - 4x + 4) – 4] = -[(x – 2)² -4] = = -(x -2) ² + 4 y = -(x -2) ² + 4 , x (2; 4) - вершина параболы х = 2 – ось симметрии параболы 3) y = p - уравнение прямой, параллельной оси Ох](https://fsd.multiurok.ru/html/2025/07/10/s_68700c29ece18/img5.jpg)
Задача№2. При каких значениях p прямая y = p имеет три общие точки с графиком функции y = f(x),
где f(x) =
Решение.
Построим график функции
f(x) =
1) y = x(x - 4) = x²- 4x = (x²- 4x +4) – 4 = (x – 2)² - 4
y = (x – 2)² - 4 , x 0
(2; -4) - вершина параболы х = 2 – ось симметрии параболы
2) y = x(4 – x) = -x² +4x = -(x² - 4x) = -[(x² - 4x + 4) – 4] = -[(x – 2)² -4] =
= -(x -2) ² + 4
y = -(x -2) ² + 4 , x
(2; 4) - вершина параболы х = 2 – ось симметрии параболы
3) y = p - уравнение прямой, параллельной оси Ох

y
y = f(x)
y = p (p= 0)
x
y = p (p= -4)
Из рисунка видно, что прямая y = p имеет три общие точки с графиком функции y = f(x) при -4
Ответ: при -4

Задания для самостоятельного решения
- Постройте график функции , где
При каких значениях m прямая m имеет с графиком этой функции две общие точки.
Ответ : при m = 0; m = 4.

Задача №3. Сколько корней имеет уравнение
x 2 -2x-3 = a в зависимости от значения параметра а ?
Решение.
Решим графически. Построим график левой и правой части уравнения
y = x 2 -2x-3 и y = a
- y= x 2 - 2x-3=(x 2 -2x+1)-1-3=(x-1) 2 -4
y = (x-1) 2 - 4 –уравнение параболы, ветви которой направлены вверх, так как a =1 0
(1;-4) – вершина параболы
- Для того чтобы построить график функции y = x 2 -2x-3 , необходимо точки, лежащие на оси Оx и часть графика, находящуюся выше оси Ox, оставить без изменения, а часть графика находящуюся ниже оси Ox, симметрично отобразить в верхнюю полуплосктость.
- y = a – уравнение прямой, параллельной оси Ox
 4) y = 4 (a = 4) y = a (0 x y = 0 (a = 0) Ответ: 1) при a =0, а (4;+ ) - два корня 2) при а (0;4) - четыре корня 3) при а =4 - три корня 4) при а (- ;0) - корней нет. y = a (a" width="640"
4) y = 4 (a = 4) y = a (0 x y = 0 (a = 0) Ответ: 1) при a =0, а (4;+ ) - два корня 2) при а (0;4) - четыре корня 3) при а =4 - три корня 4) при а (- ;0) - корней нет. y = a (a" width="640"
y
y = x 2 -2x-3
y = a (a 4)
y = 4 (a = 4)
y = a (0
x
y = 0 (a = 0)
Ответ:
1) при a =0, а (4;+ ) - два корня
2) при а (0;4) - четыре корня
3) при а =4 - три корня
4) при а (- ;0) - корней нет.
y = a (a
 7 2. Определите количество корней уравнения |2x 2 + 4x - 7|= a при всех положительных значениях параметра а . Ответ: 4 корня при 0 3 корня при a = 9 2 корня при a 9 " width="640"
7 2. Определите количество корней уравнения |2x 2 + 4x - 7|= a при всех положительных значениях параметра а . Ответ: 4 корня при 0 3 корня при a = 9 2 корня при a 9 " width="640"
Задания для самостоятельного решения
1. Определите количество корней уравнения |x 2 - 4x - 3|= a при всех положительных значениях параметра a . Ответ: 4 корня при 0 3 корня при a = 7 2 корня при a 7 2. Определите количество корней уравнения |2x 2 + 4x - 7|= a при всех положительных значениях параметра а . Ответ: 4 корня при 0 3 корня при a = 9 2 корня при a 9

Задача №4. Построить график функциии определите,
при каких значениях параметрапрямая не имеет с графиком функции общих точек.
Решение.
Построим график функции
1)
2)
=

3)
В новой системе координат с началом в точке построим гиперболу
Составим таблицу значений для графика функции в новой системе координат
4) у = а – уравнение прямой, параллельной оси Ох
х
х
y
y
-8
-8
-4
-4
-
-2
-
-2
-1
-1
-1
-1
-2
-2
-
-4
-4
-
-8
-8
8
8
4
4
1
1
2
2
2
2
1
4
4
1
8
8

y
y= a
1
3
5
y= a ( a = -1)
x
-1
y= a ( a = -2)
y= a
Ответ: при a = -2; a = -1 прямая не имеет с графиком функции общих точек

Задания для самостоятельного решения
1. Постройте график функции y=
Найдите значения b, при которых прямая у = b не имеет с графиком данной функции общих точек
Ответ : при b = -2; b = -1
2. Постройте график функции и определите, при каких значениях a прямая у=а не имеет с графиком ни одной общей точки
a) у =
Ответ : при а = 4; а =3
b) у =
Ответ : при а = 5; а = 5

Задача№5. Постройте график функции у= и определите, при каких значениях k прямая у=kх имеет с графиком ровно одну общую точку
Решение.
Построим график функции у==
- D (у): х 0; х -
- y= = =
у = (х 0)– уравнение гиперболы
3 ) y=kx – уравнение прямой, проходящей через начало координат
х
х
у
у
-4
-4
-2
-
-2
-1
-1
-
-1
-1
-
-2
-2
-
-4
-4
4
4
2
1
1
2
1
1
2
2
4
4

4) Прямая y = kx имеет с данным графиком функции ровно одну общую точку, если она проходит через точку с абсциссой равной
Найдем ординату этой точки:
y
y=kx
y=kx
y=kx (k=)
x
-1
-1
5) Найдем угловой коэффициент прямой, проходящей через точку ;
k=
Ответ: при k=

Задания для самостоятельного решения
1. Постройте график функции и определите, при каких значениях k прямая у=kx имеет с графиком ровно одну общую точку
a) у=
Ответ : при k = 81
b) у=
Ответ : при k =

Задача№6. Постройте график функции у= и определите, при каких значениях m прямая y=mимеет с графиком ровно две общие точки.
Решение:
- Построим график функции у=(х+1)-5х
D( y )=R
Т.к функция содержит один знак модуля, то раскроем знак модуля по определению, получим:
y =
y =
y =

1) ,
;
(-3;9)-вершина параболы
2)
(2;-4)-вершина параболы
2. = m - уравнение прямой, параллельной оси О x

y
y=m (m = 9)
у=
y=m
x
y=m
y=m (m = -4)
y=m
Ответ: при m = - 4; m = 9

Задания для самостоятельного решения
1. Постройте график функции и определите, при каком значении m прямая y=m имеет с графиком ровно две общие точки
a) y= | x | (x+1)-6x
Ответ: при m = -6,25; m = 12,25
b) y=|x|x -|x|- 6x
Ответ: при m = -12,25; m = 6,25
2. Постройте график функции y=x 2 - 8x - 4|x - 3|+15
и определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки
Ответ: при m=-1, m=0

Задача№7. Построить график функции
и определите, при каких значениях k прямая =не имеет с графиком общих точек
Решение. т.к =
или
4

2. y==
y=
1) y= ()- уравнение гиперболы
2) Для того чтобы построить график функции у= необходимо точки, лежащие на оси Oу, и часть графика, лежащего правее на оси Оу, оставить без изменения, левую часть графика стереть. Для правой части графика построить симметричную относительно оси Оу.
3. ykx– уравнение прямой, проходящей через начало координат.
х
х
-4
-4
y
y
-2
-2
-1
-1
1
1
-
-
2
2
4
4
-4
-4
-2
1
-2
1
2
2
-1
-1
4
4
-
-

4. Прямая y=kx не имеет с графиком функции общих точек, если она проходит через точки с абсциссами . А так же когда совпадает с осью Ox, в этом случае k=0.
5. Найдем ординаты этих точек:
х= ; y = =
х= ; y = − = 4
6.Найдите угловой коэффициент прямой y=kx проходящий через точки
k =4
k =16 k =16
Ответ: при k =-16; k =0; k =16

y
y = k(k = 16)
y = k(k = -16)
y = k
-1
y=k (k=0)
x
1
y=
-4

Задания для самостоятельного решения
1. Постройте график функции и определите, при каких значениях kпрямая y=kxне имеет с графиком общих точек
Ответ: при k =- 2,25; k = 0; k =2,25
2. Постройте график функциии определите, при каких значениях k прямая y=kxне имеет с графиком общих точек
Ответ: при k =- 6,25;k =0; k = 6,25












![Задача№2. При каких значениях p прямая y = p имеет три общие точки с графиком функции y = f(x), где f(x) = Решение. Построим график функции f(x) = 1) y = x(x - 4) = x²- 4x = (x²- 4x +4) – 4 = (x – 2)² - 4 y = (x – 2)² - 4 , x 0 (2; -4) - вершина параболы х = 2 – ось симметрии параболы 2) y = x(4 – x) = -x² +4x = -(x² - 4x) = -[(x² - 4x + 4) – 4] = -[(x – 2)² -4] = = -(x -2) ² + 4 y = -(x -2) ² + 4 , x (2; 4) - вершина параболы х = 2 – ось симметрии параболы 3) y = p - уравнение прямой, параллельной оси Ох](https://fsd.multiurok.ru/html/2025/07/10/s_68700c29ece18/img5.jpg)



 4) y = 4 (a = 4) y = a (0 x y = 0 (a = 0) Ответ: 1) при a =0, а (4;+ ) - два корня 2) при а (0;4) - четыре корня 3) при а =4 - три корня 4) при а (- ;0) - корней нет. y = a (a" width="640"
4) y = 4 (a = 4) y = a (0 x y = 0 (a = 0) Ответ: 1) при a =0, а (4;+ ) - два корня 2) при а (0;4) - четыре корня 3) при а =4 - три корня 4) при а (- ;0) - корней нет. y = a (a" width="640"
 7 2. Определите количество корней уравнения |2x 2 + 4x - 7|= a при всех положительных значениях параметра а . Ответ: 4 корня при 0 3 корня при a = 9 2 корня при a 9 " width="640"
7 2. Определите количество корней уравнения |2x 2 + 4x - 7|= a при всех положительных значениях параметра а . Ответ: 4 корня при 0 3 корня при a = 9 2 корня при a 9 " width="640"


























