Россия, п.Новосельский
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до 18.04.2025
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 13.04.2025 16:58
Нуркатова Гульсара Дуйсембаевна
учитель математики
80
217 931 
Местоположение
Специализация
Презентация по алгебре на тему "Решение квадратных уравнений" (8 класс)
Категория:
Алгебра
02.04.2025 11:33
Просмотр содержимого документа
«Презентация по алгебре на тему "Решение квадратных уравнений" (8 класс)»
Решение квадратных уравнений
«Квадратные уравнения - это фундамент, на котором покоится величественное здание алгебры».
Леонардо Фибоначчи
Психологическая установка на урок:
« Понять и быть тем первым, который увидит ход решения»
Устный счет
(х 1 = 1 , х 2 = -24 )
- х² +23x-24=0
- 2х² + x-3=0
- х² +3x+2=0
- 5х² +8x+3=0
(х 1 = 1 , х 2 = -1,5 )
(х 1 = -1 , х 2 = -2 )
(х 1 = -1 , х 2 = -0,6 )
Устный счет
- √ 169
- √ 121
- √ 4900
(13 )
(11 )
(70 )
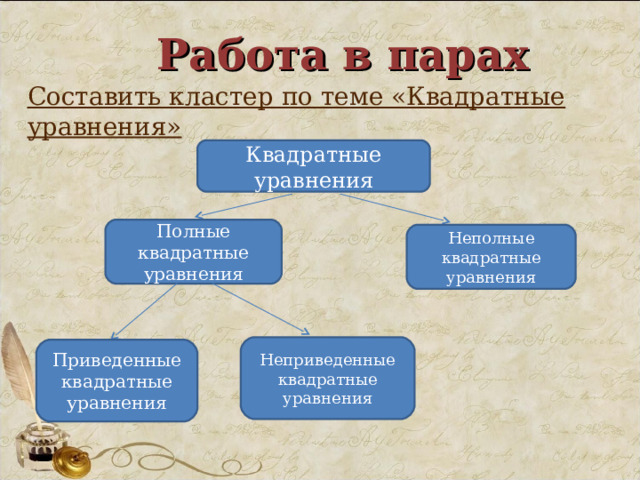
Работа в парах
Составить кластер по теме «Квадратные уравнения»
Квадратные уравнения
Полные квадратные уравнения
Неполные квадратные уравнения
Неприведенные квадратные уравнения
Приведенные квадратные уравнения
0, то уравнение имеет 2 корня " width="640"
Полное квадратное уравнение
a x 2 + b x+ c= 0
D = b 2 - 4ac
Если D
Если D = 0, то уравнение имеет 1 корень
Если D 0, то уравнение имеет 2 корня
Неполные квадратные уравнения
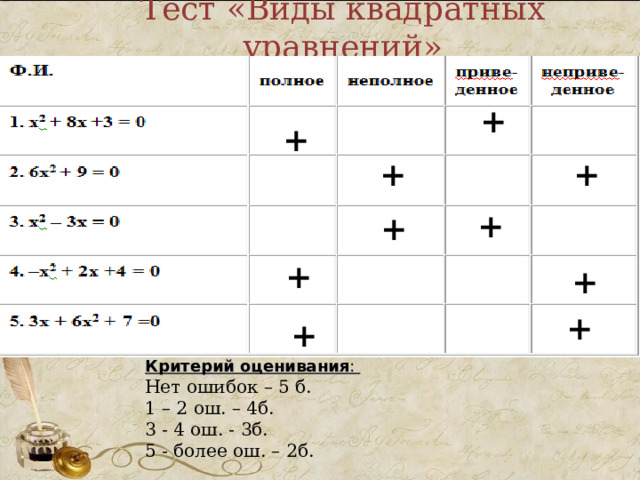
Тест «Виды квадратных уравнений»
+
+
+
+
+
+
+
+
+
+
Критерий оценивания :
Нет ошибок – 5 б.
1 – 2 ош. – 4б.
3 - 4 ош. - 3б.
5 - более ош. – 2б.
Задание на соответствие:
1 - 4
2 - 7
3 - 1
4 - 6
5 - 3
6 - 5
7 - 2
Карточка -теоретические вопросы
- 1) Общий вид квадратного уравнения.
- 2) Формула дискриминанта.
- 3) Формула для вычисления корней квадратного уравнения.
- 4) Формула для вычисления дискриминанта квадратного уравнения с четным вторым коэффициентом.
- 5) Формула для вычисления корней квадратного уравнения c четным вторым коэффициентом.
- 6) Формула разложения трехчлена на множители.
- 7) Теорема Виета для квадратного уравнения вида ax 2 + bx + c = 0
- 8) Теорема Виета для приведенного квадратного уравнения x 2 + px + g = 0
Практикум - «Скоро экзамен»
- Региональный экзамен 8 кл
Часть 1
3 вариант
№ 5 Решите уравнение:
Х 2 + 18 х + 65 = 0
5 вариант
№ 5 Найдите положительные корни уравнения 64х – 4 х 2 = 0
Физкультминутка
Работа в группах.
1 группа
Решить квадратные уравнения
а) З х 2 + 6 =0; б) Х 4 + 5х 2 – 36 =0
2 группа
Решить квадратные уравнение:
а) 4х – 100 =0; б) 3(х + 6) + 2010(х + 6) – 2013 = 0
3 группа
Решить квадратные уравнения
а) х 2 +2 х = 0; б)4x 2 – 1 7x – 15 = 0 (метод переброски)
«Синквейн»
- Одно слово. Существительное или местоимение, обозначающее предмет, о котором идет речь.
- Два слова. Прилагательные или причастия, описывающие признаки и свойства выбранного предмета.
- Три слова . Глаголы, описывающие совершаемые предметом или объектом действия.
- Фраза из четырех слов . Выражает личное отношение автора к предмету или объекту.
- Одно слово. Характеризует суть предмета или объекта.
Дифференцированное д омашнее задание
Фамилия, имя ______________________________________ 1) Решить три уравнения (любым способом) Решения уравнений записать в тетрадь. 1 уровень – № 1, 2, 3 2 уровень – № 2, 3, 4 3 уровень – № 3, 4, 5
Критерии оценок
- от 18 баллов «5»
- 11 – 17 баллов «4»
- 6 – 10 баллов «3»
- «Человеку, изучающему алгебру, часто полезнее решить одну и ту же задачу тремя различными способами, чем решить три-четыре различные задачи. Решая одну задачу различными методами, можно путем сравнений выяснить, какой из них короче и эффективнее. Так вырабатывается опыт».
У. Сойер
Спасибо
за урок!
© 2025, Нуркатова Гульсара Дуйсембаевна 60 1
Рекомендуем курсы ПК и ППК для учителей
Похожие файлы
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
Полезное для учителя
Реализация образовательных программ осуществляется с применением исключительно электронного обучения и ДОТ
