Презентация по геометрии на тему "Параллельность плоскостей. Свойства параллельных плоскостей" (10 класс)

10 класс ГЕОМЕТРИЯ

Автор презентации: Попов Дмитрий Сергеевич

Ваша задача на сегодня:

• Откройте тетради, запишите дату и тему урока.
• Выпишите теоремы и определения.
• Выполните задания на слайдах 16-17.
• Выполните домашнее задание.

Как известно из аксиом стереометрии, если плоскости имеют одну общую точку, то они пересекаются по прямой, проходящей через эту точку. Значит две плоскости или пересекаются, или не пересекаются.

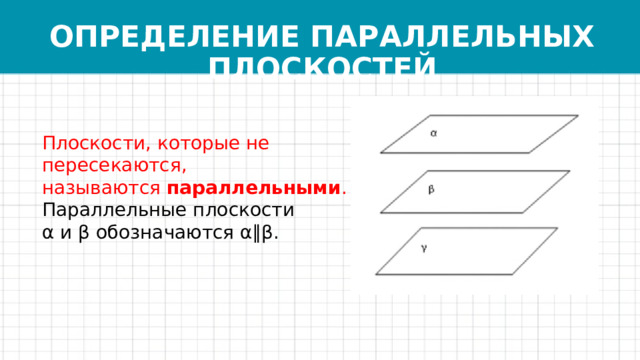
ОПРЕДЕЛЕНИЕ ПАРАЛЛЕЛЬНЫХ ПЛОСКОСТЕЙ

Плоскости, которые не пересекаются, называются  параллельными .

Параллельные плоскости α и β обозначаются α∥β.

ПАРАЛЛЕЛЬНОСТЬ ПЛОСКОСТЕЙ В РЕАЛЬНОЙ ЖИЗНИ

Любая конструкция с полом, потолком и стенами даёт нам представление о параллельных плоскостях – пол и потолок как две параллельные плоскости, боковые стены как параллельные плоскости.

ПРИЗНАК ПАРАЛЛЕЛЬНОСТИ ПЛОСКОСТЕЙ

Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны.

Доказательство.

Пусть α и β - данные плоскости, a 1  и a 2  – пересекающиеся прямые в плоскости α, а b 1  и b 2  соответственно параллельные им прямые в плоскости β. 

Допустим, что плоскости α и β не параллельны, то есть они пересекаются по некоторой прямой c.

Прямая a 1  параллельна прямой b 1 , значит она параллельна и самой плоскости β.

Прямая a 2  параллельна прямой b 2 , значит она параллельна и самой плоскости β (признак параллельности прямой и плоскости).

  Прямая c принадлежит плоскости α, значит хотя бы одна из прямых a 1  или a 2  пересекает прямую c, то есть имеет с ней общую точку. Но прямая c также принадлежит и плоскости β, значит, пересекая прямую c, прямая a 1  или a 2  пересекает плоскость β, чего  быть не может , так как прямые a 1  и a 2  параллельны плоскости β.

Из этого следует, что плоскости α и β не пересекаются, то есть они  параллельны . 

Теорема доказана.

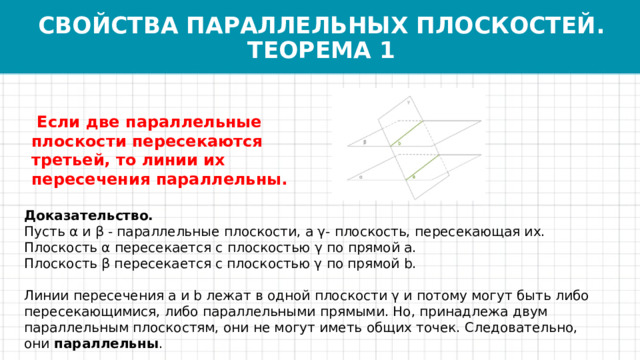
СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПЛОСКОСТЕЙ. ТЕОРЕМА 1

  Если две параллельные плоскости пересекаются третьей, то линии их пересечения параллельны.

Доказательство. 

Пусть α и β - параллельные плоскости, а γ- плоскость, пересекающая их.

Плоскость α пересекается с плоскостью γ по прямой a.  

Плоскость β пересекается с плоскостью γ по прямой b. 

Линии пересечения a и b лежат в одной плоскости γ и потому могут быть либо пересекающимися, либо параллельными прямыми. Но, принадлежа двум параллельным плоскостям, они не могут иметь общих точек. Следовательно, они  параллельны .

СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПЛОСКОСТЕЙ. ТЕОРЕМА 2

Отрезки параллельных прямых, заключенных между двумя параллельными плоскостями, равны.

Доказательство.

Пусть α и β - параллельные плоскости, а a и b – параллельные прямые, пересекающие их.

Через прямые a и b можно провести плоскость - эти прямые параллельны, значит определяют плоскость, причём только одну.

Проведённая плоскость пересекается с плоскостью α по прямой AB, а с плоскостью β по прямой CD. 

По предыдущей теореме прямые AB и CD параллельны. Четырехугольник ABCD есть параллелограмм (у него противоположные стороны параллельны). А раз это параллелограмм, то противоположные стороны у него  равны , то есть BC=AD.

СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПЛОСКОСТЕЙ. ТЕОРЕМА 3

Если прямая пересекает одну из двух параллельных плоскостей, то она пересекает и другую.

Доказательство.

Пусть α||β, a пересекает α в точке А.

Выберем в плоскости любую точку  C . Через эту точку и прямую  a  проведём плоскость.

Так как плоскость имеет с плоскостями α и β общие точки  A  и  C  соответственно, то она пересекает эти плоскости по некоторым прямым  b  и  c , которые проходят соответственно через точки  A  и  C . По предыдущей теореме прямые  b  и  c  параллельны. Тогда в плоскости прямая  a  пересекает (в точке  A ) прямую  b , которая параллельна прямой  c . Значит, прямая  a  пересекает и прямую  c  в некоторой точке  B . Так как прямая  c  лежит в плоскости, то точка  B  является точкой пересечения прямой  a  и плоскости. Теорема доказана.

СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПЛОСКОСТЕЙ. ТЕОРЕМА 4

Если плоскость пересекает одну из двух параллельных плоскостей, то она пересекает и другую плоскость.

Доказательство. Пусть α||β, α и γ пересекаются.

Докажем, что плоскости β и γ пересекаются.

Проведём в плоскости γ прямую  a , пересекающую плоскость α в некоторой точке  B . Тогда по теореме 3 прямая  a  пересекает и плоскость β в некоторой точке  A . Следовательно, плоскости β и γ имеют общую точку  A , т. е. пересекаются. Теорема доказана. 

СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПЛОСКОСТЕЙ. ТЕОРЕМА 5

Через точку, не лежащую в данной плоскости, можно провести плоскость, параллельную данной, и притом только одну.

ДОКАЗАТЕЛЬСТВО. Пусть нам даны плоскость α и точка М, ей не принадлежащая.

Докажем, что существует плоскость β, которой принадлежит точка М, параллельная плоскости α.

В данной плоскости α проведём две произвольные пересекающиеся прямые  a  и  b . Через точку  M  проведём прямые  a 1  и  b 1 , параллельные соответственно  a  и  b . Плоскость, проходящую через пересекающиеся прямые  a 1  и  b 1 , обозначим β. На основании признака параллельности плоскостей плоскость β параллельна плоскости α.

Докажем методом от противного, что β — единственная плоскость, удовлетворяющая условию теоремы.

Допустим, что через точку  M  проходит другая плоскость, например β 1 , параллельная α.

Так как β 1  пересекает плоскость β (они имеют общую точку  M ), то по теореме 4 плоскость β 1  пересекает и плоскость α (β ‖ α). Мы пришли к противоречию. Таким образом, предположение о том, что через точку  M  можно провести плоскость, отличную от плоскости β и параллельную плоскости α, неверно. Значит, плоскость β — единственна. Теорема доказана. 

Рассмотрим несколько простых задач на доказательство.

Даны две пересекающиеся прямые a и b точка А, не лежащая в плоскости этих прямых. Докажите, что через точку А проходит плоскость, параллельная прямым a и b, и притом только одна.

Доказательство.

Прямые a и b пересекаются по условию, следовательно, эти прямые единственным образом определяют плоскость α.

Известно, что через точку А, не принадлежащую плоскости α, проходит единственная плоскость, параллельная α, т.е. параллельная прямым a и b   (по теореме 5)  .

Плоскости α и β параллельны, прямая m лежит в плоскости α. Докажите, что прямая m параллельна плоскости β.

Доказательство.

Предположим, что прямая m пересекает плоскость β в точке М. Тогда точка М принадлежит плоскости α (т.к. прямая m лежит в плоскости α) и М принадлежит плоскости β, значит, α и β пересекаются, но они параллельны по условию. Очевидно, m не пересекает плоскость α, т.е. параллельна ей.

Три отрезка А 1 А 2 , В 1 В 2  и С 1 С 2 , не лежащие в одной плоскости, имеют общую середину. Докажите, что плоскости А 1 В 1 С 1  и А 2 В 2 С 2  параллельны.

Докажем параллельность А 1 В 1  и А 2 В 2 .

Рассмотрим плоскость, проходящую через прямые А 1 А 2  и В 1 В 2

(она существует и единственная, т.к. прямые пересекаются).

В этой плоскости лежит четырехугольник А 1 В 1 А 2 В 2 , диагонали которого точкой пересечения делятся пополам. Следовательно, данный четырехугольник является параллелограммом (признак параллелограмма), значит, А 1 В 1  и А 2 В 2  параллельны.

Аналогично доказывается параллельность В 1 С 1  и В 2 С 2 . Из вышеперечисленного следует, что плоскости А 1 В 1 С 1  и А 2 В 2 С 2  параллельны по признаку параллельности плоскостей.

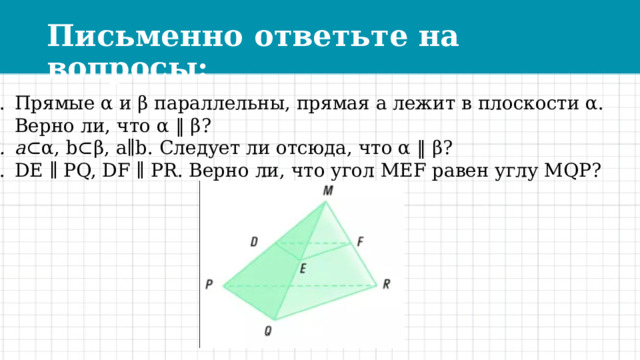
Письменно ответьте на вопросы:

• Прямые α и β параллельны, прямая а лежит в плоскости α. Верно ли, что α ‖ β?
• a ⊂α, b⊂β, a∥b. Следует ли отсюда, что α ‖ β?
• DE ∥ PQ, DF ∥ PR. Верно ли, что угол MEF равен углу MQP?

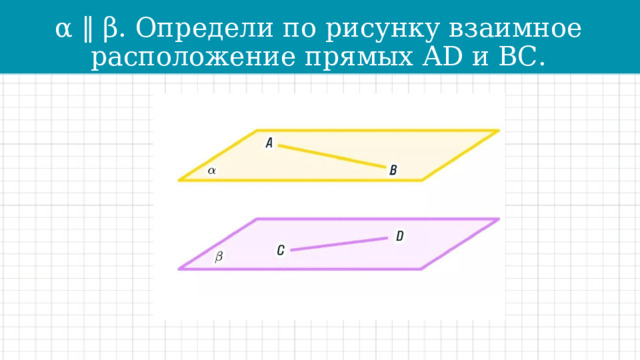
α ‖ β. Определи по рисунку взаимное расположение прямых АD и ВС.

Рефлексия

Домашнее задание

1) Прочитайте п. 10,11; 2) Выполните №63(а).