Презентация по теме "Алгебра логики"

Алгебра логики

Высказывание

Логические операции

Высказывание

П редложение на любом языке, содержание которого можно однозначно определить как истинное или ложное .

Высказывание

Истинное (1)

Ложное (0)

Логические операции

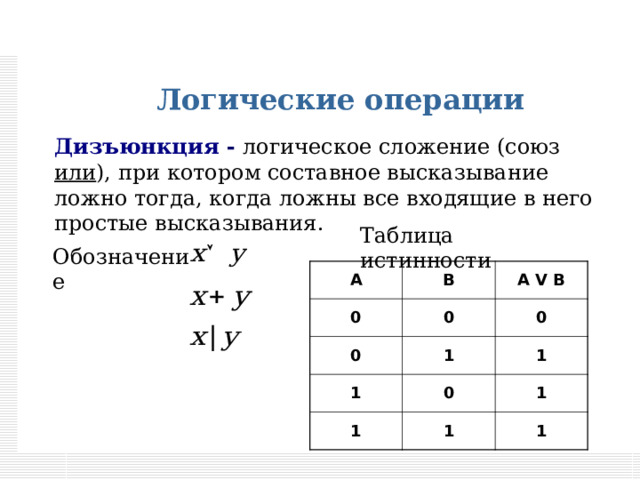
Дизъюнкция - логическое сложение (союз или ), при котором составное высказывание ложно тогда, когда ложны все входящие в него простые высказывания.

Таблица истинности

Обозначение

А

0

В

А V B

0

0

1

0

1

1

0

1

1

1

1

Логические операции

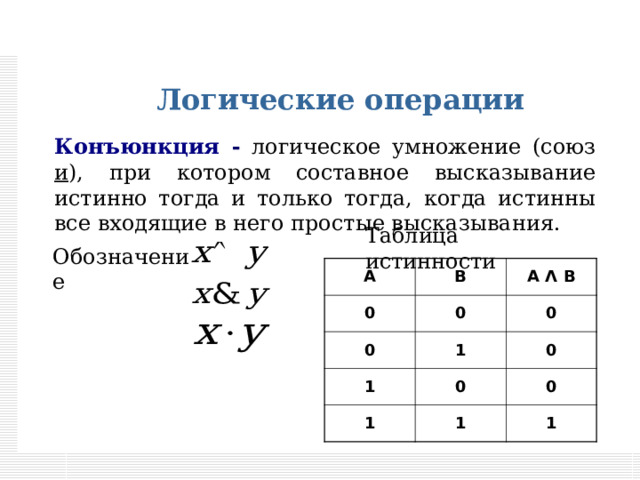
Конъюнкция - логическое умножение (союз и ), при котором составное высказывание истинно тогда и только тогда, когда истинны все входящие в него простые высказывания.

Таблица истинности

Обозначение

А

0

В

А Λ B

0

0

1

0

1

1

0

0

0

1

1

Логические операции

Импликация - (логическое следование - если…, то…). Ложно тогда и только тогда, когда из истинного высказывания следует ложное.

Таблица истинности

Обозначение

x → y

А

0

В

А → B

0

0

1

1

1

1

1

0

0

1

1

Логические операции

Эквиваленция - (логическое равенство (тождество) - тогда и только тогда…). Истинно тогда и только тогда, когда оба высказывания истины или оба ложны.

Таблица истинности

Обозначение

x ↔ y

А

0

В

0

А ↔ B

0

1

1

1

1

0

0

0

1

1

x ≡ y

Логические операции

Инверсия - (отрицание) делает истинное высказывание ложным, а ложное истинным.

Таблица истинности

Обозначение

А

0

¬ А

1

1

0

Последовательность операций

• Инверсия ¬ (отрицание)
• Конъюнкция /\ («И» умножение)
• Дизъюнкция \/ («ИЛИ» сложение)
• Импликация → (следование)
• Эквиваленция ↔ (равенство)

Приоритет операций можно изменить при помощи скобок.

Решение задач 1

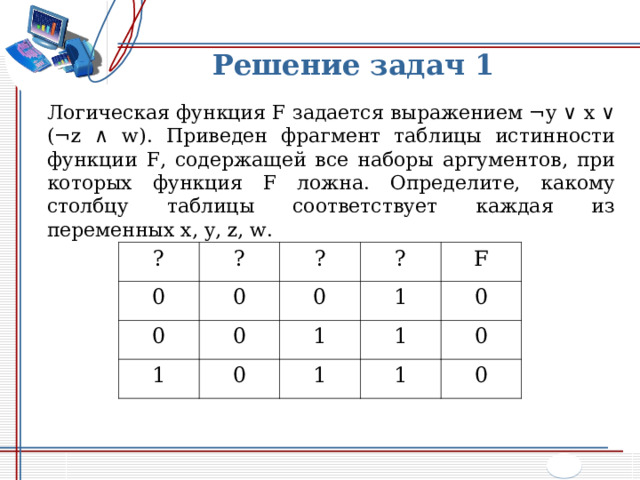
Логическая функция F задается выражением ¬ y ∨ x ∨ ( ¬ z ∧ w) . Приведен фрагмент таблицы истинности функции F , содержащей все наборы аргументов, при которых функция F ложна. Определите, какому столбцу таблицы соответствует каждая из переменных x, y, z, w .

?

0

?

0

?

0

1

0

?

0

1

F

1

0

0

1

1

0

1

0

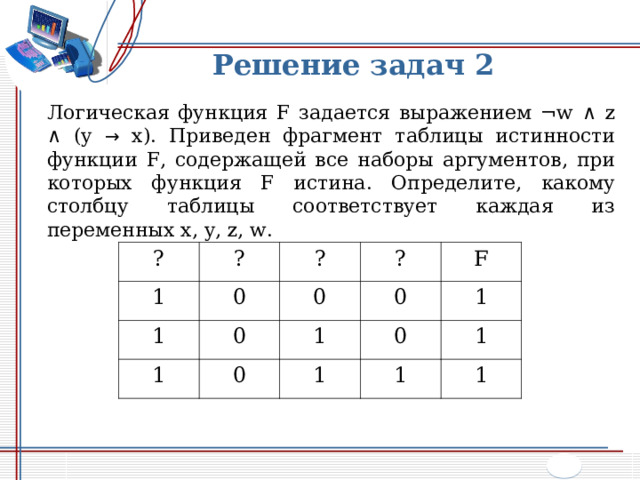
Решение задач 2

Логическая функция F задается выражением ¬ w ∧ z ∧ (y → x) . Приведен фрагмент таблицы истинности функции F , содержащей все наборы аргументов, при которых функция F истина. Определите, какому столбцу таблицы соответствует каждая из переменных x, y, z, w .

?

1

?

1

?

0

1

0

?

0

0

F

1

0

1

0

1

1

1

1

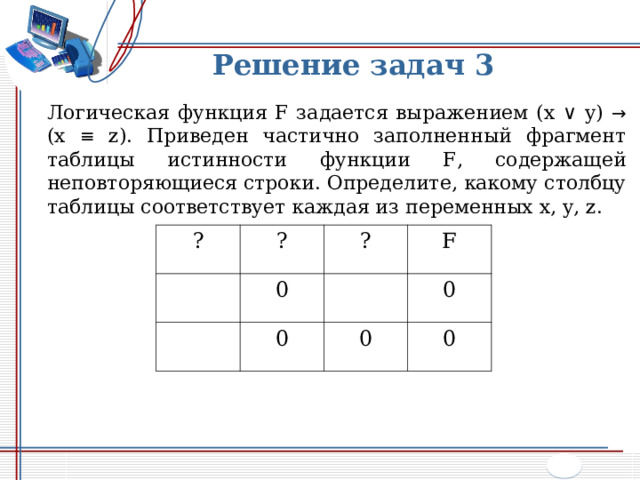
Решение задач 3

Логическая функция F задается выражением ( x ∨ y) → (x ≡ z) . Приведен частично заполненный фрагмент таблицы истинности функции F , содержащей неповторяющиеся строки. Определите, какому столбцу таблицы соответствует каждая из переменных x, y, z .

?

?

?

0

F

0

0

0

0

Решение задач 4

Логическая функция F задается выражением ( x → ( y ∧ ¬ z)) ∨ w . Приведен частично заполненный фрагмент таблицы истинности функции F , содержащей неповторяющиеся строки. Определите, какому столбцу таблицы соответствует каждая из переменных x, y, z .

?

?

0

?

1

?

1

F

0

0

1

1

0

0

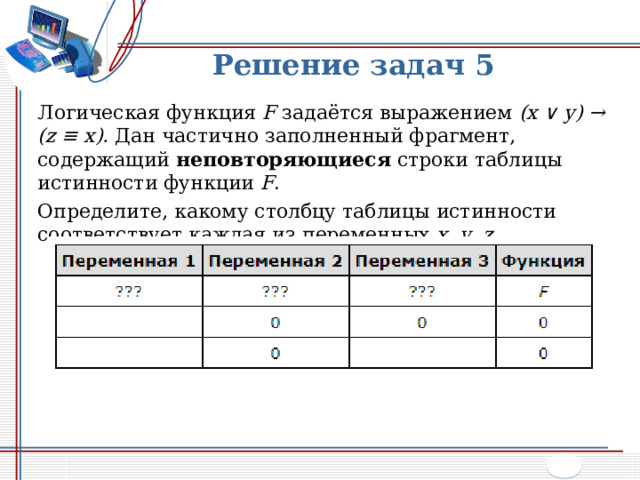
Решение задач 5

Логическая функция  F  задаётся выражением  (x ∨ y) → (z ≡ x). Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции  F .

Определите, какому столбцу таблицы истинности соответствует каждая из переменных  x ,  y ,  z .

Решение задач 6

Логическая функция  F  задаётся выражением ( x  ≡  z  ) ∨ ( x  → ( y  ∧  z )).

Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции  F .

Определите, какому столбцу таблицы истинности соответствует каждая из переменных  x ,  y ,  z .

Решение задач 7

Логическая функция  F  задаётся выражением ( x  ≡  y  ) ∨ (( y  ∨  z ) →  x ).

Дан частично заполненный фрагмент, содержащий неповторяющиеся  строки таблицы истинности функции  F .

Определите, какому столбцу таблицы истинности соответствует каждая из переменных  x ,  y ,  z .