Презентация по теме "Функции. Пределы. Производные", 12 класс

∆х= х 2 - х 1 . Геометрически приращение аргумента изображается приращением абсциссы точки кривой, а приращение функции – приращение ординаты этой точки. " width="640"

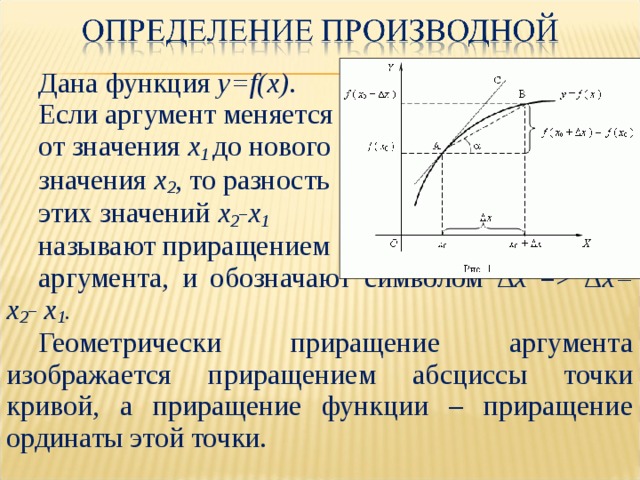
Дана функция y = f ( x ) .

Если аргумент меняется

от значения х 1 до нового

значения х 2 , то разность

этих значений х 2 -х 1

называют приращением

аргумента, и обозначают символом ∆х = ∆х= х 2 - х 1 .

Геометрически приращение аргумента изображается приращением абсциссы точки кривой, а приращение функции – приращение ординаты этой точки.

Производной функции в точке x 0 называется предел отношения приращения функции к приращению аргумента, если приращение аргумента стремится к нулю .

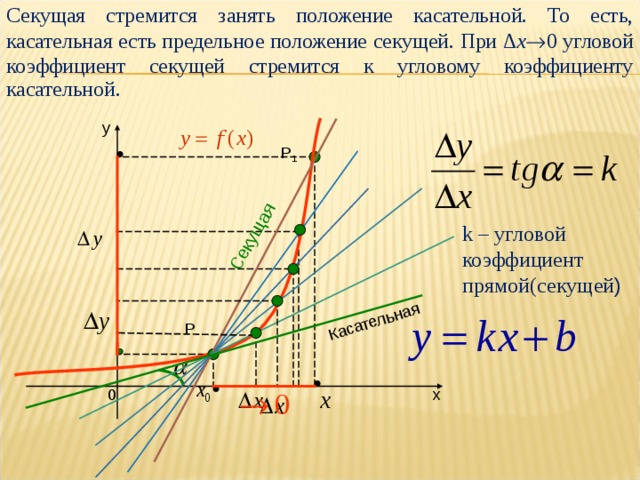
Секущая стремится занять положение касательной. То есть, касательная есть предельное положение секущей. При ∆ x  0 угловой коэффициент секущей стремится к угловому коэффициенту касательной.

Секущая

Касательная

y

Р 1

k – угловой коэффициент прямой(секущей )

Р

0

х

Если функции U и V дифференцируемы в точке x 0 , то

из второго свойства следует (С U)´=CU´ , где С – постоянная.

• Если функции U и V дифференцируемы в точке x 0 , то из второго свойства следует (С U)´=CU´ , где С – постоянная.

• ( U + V )´ = U´ + V´

• (U V)´ = U´ V + U V´

• U ´ U´ V - U V´

— = ——————

V V 2

Если функция y=f(z) имеет производную в точке z , a z=g(x) имеет производную в точке x , то функция y=f(g(x)) имеет производную в точке x и y'=f '(g(x))g'(x) .

Доказательство:

Пусть функция f(x) имеет в точке x o производную f '(x)  0 . Тогда обратная функция g(y) имеет в точке y 0 производную g'(y 0 )=1/f '(x 0 ) .

Доказательство:

1) f(x) = C .

 f(x0) = f(x0 +  x) – f(x0) = C – C = 0 ;

. Таким образом , ( С) ´ = 0 .

2) f ( x ) = x .

 f ( x 0) = f ( x 0 +  x ) – f ( x 0) = ( x 0 +  x ) – x 0 =  x ;

. Таким образом, (x) ´ = 1 .

3) f ( x ) = x n .

Прологарифмируем равенство , получим: ln f ( x ) = n ln( x ). Продифферецируем равенство , получим: f ´ (x)/f(x)=n/x . Выразим f ´ , получим f ´ (x)=f(x)n/x = x n n/x = nx n-1 . Таким образом, ( x n ) ´ = nx n-1 .

4) f(x)=sin(x)

Таким образом, (sin(x)) ´ = cos(x) .

4) f(x)=arcsin(x)

y= arcsin(x) , тогда x=sin(y). y´=1/x´

Таким образом, ( arcsin(x) ) ´ = 1/  (1-x 2 ) .

Функцию r: R  R n будем называть вектор-функцией. Т.е. r(t)= ={x 1 (t),x 2 (t),…,x n (t)}.

Теорема r´(t)={x 1 ´(t),x 2 ´(t),…,x n ´(t)} .

СВОЙСТВА ПРОИЗВОДНОЙ ВЕКТОР-ФУНКЦИИ