Презентация по теме "Объем прямой призмы и цилиндра"

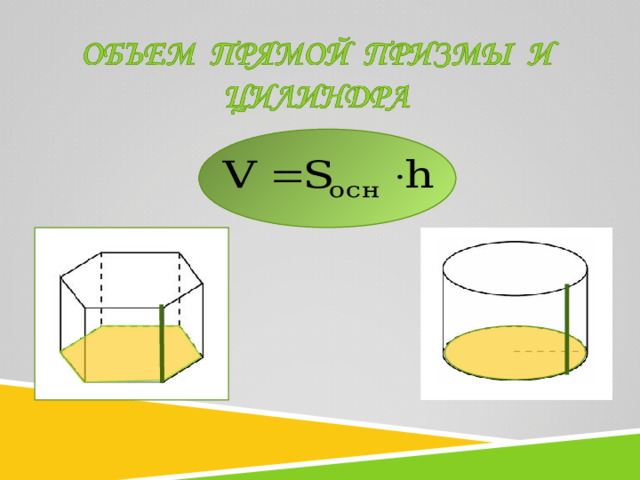
НЕКОТОРЫЕ ОТНОШЕНИЯ ПОДОБИЯ

• Отношение периметров подобных многоугольников равно коэффициенту подобия.

• Отношение площадей подобных фигур равно квадрату коэффициента подобия.

• Отношение объемов подобных тел равно кубу коэффициента подобия.

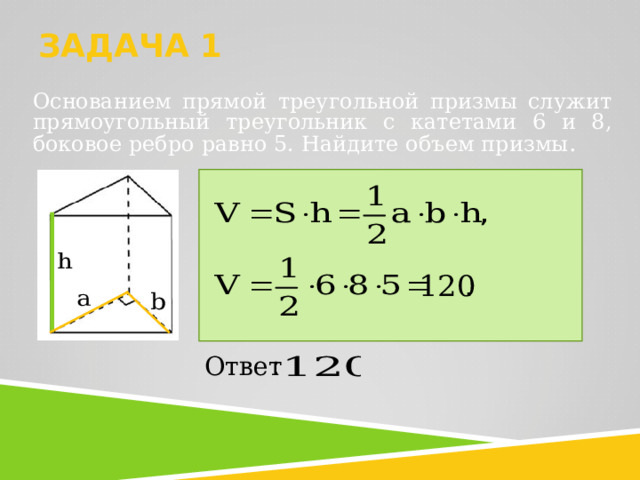
ЗАДАЧА 1

Основанием прямой треугольной призмы служит прямоугольный тре­угольник с катетами 6 и 8, боковое ребро равно 5. Найдите объем приз­мы .

ЗАДАЧА 2

Найдите объем правильной шестиугольной призмы, стороны основания которой равны 1, а боковые ребра равны √3.

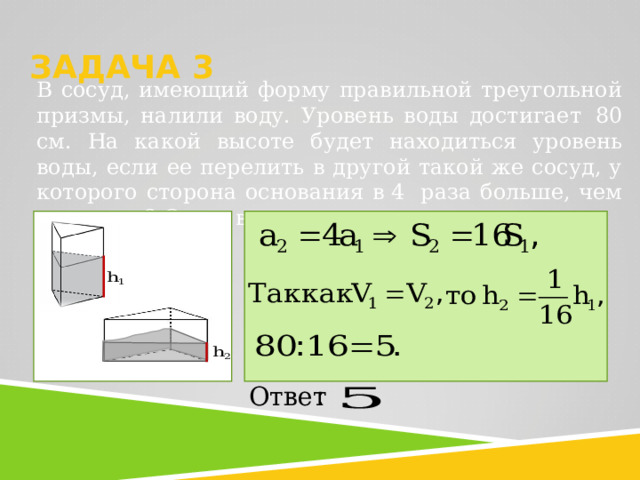
ЗАДАЧА 3

В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает   80 см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в  4  раза больше, чем у первого? Ответ выразите в см.

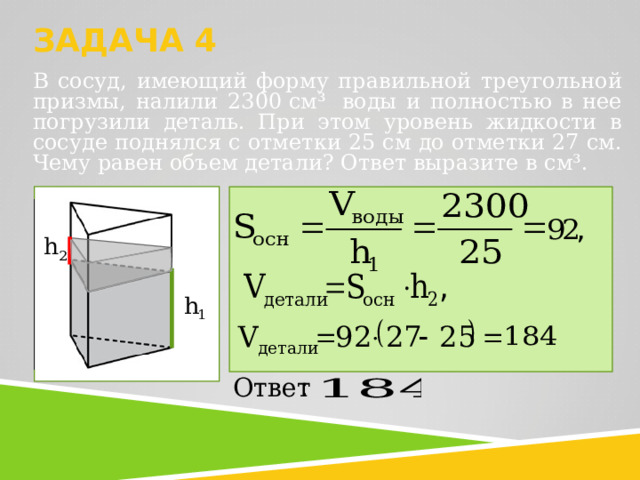
ЗАДАЧА 4

В сосуд, имеющий форму правильной треугольной призмы, налили 2300 см³  воды и полностью в нее погрузили деталь. При этом уровень жидкости в сосуде поднялся с отметки 25 см до отметки 27 см. Чему равен объем детали? Ответ выразите в см³.

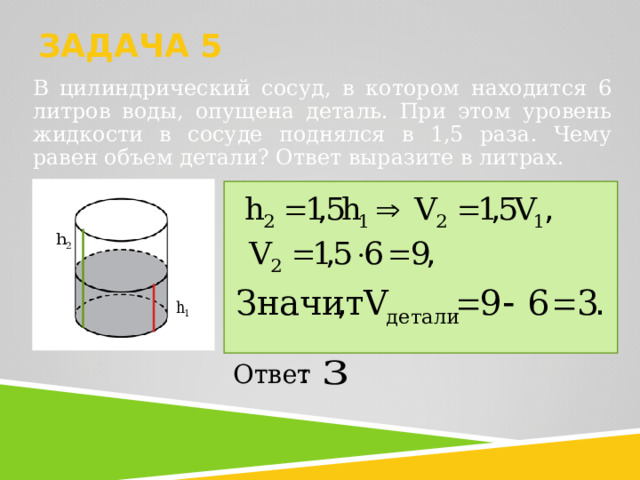
ЗАДАЧА 5

В цилиндрический сосуд, в котором находится 6 литров воды, опущена деталь. При этом уровень жидкости в сосуде поднялся в 1,5 раза. Чему равен объем детали? Ответ выразите в литрах.

ЗАДАЧА 6

Объем первого цилиндра равен 12 м 3 . У второго цилиндра высота в три раза больше, а радиус основания — в два раза меньше, чем у первого. Найдите объем второго цилиндра. Ответ дайте в кубических метрах.

ЗАДАЧА 7

Найдите объем  V  части цилиндра, изображенной на рисунке. В ответе укажите V/ π .

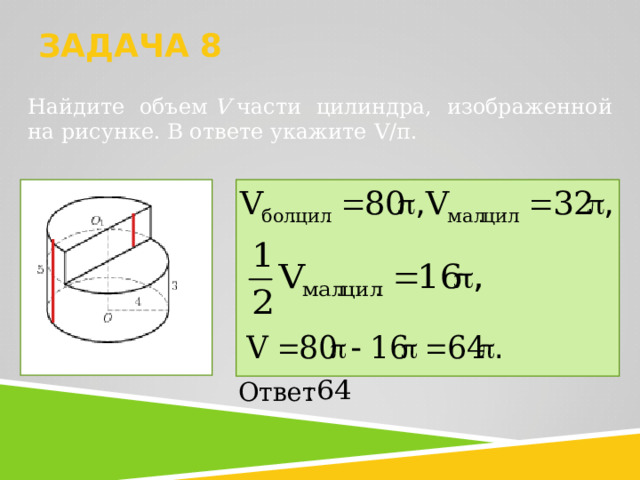
ЗАДАЧА 8

Найдите объем  V  части цилиндра, изображенной на рисунке. В ответе укажите V/ π .

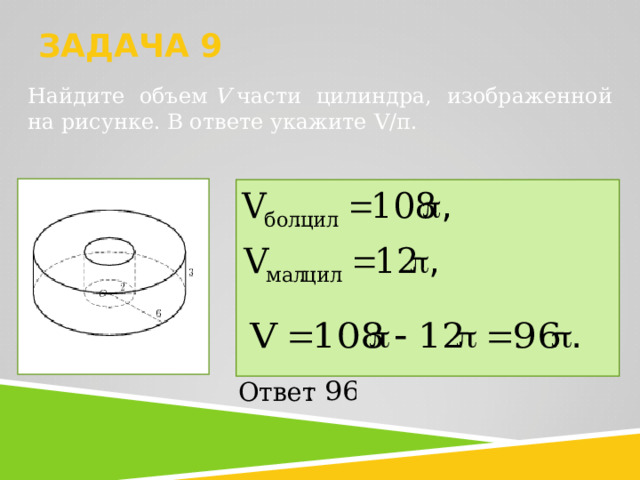
ЗАДАЧА 9

Найдите объем  V  части цилиндра, изображенной на рисунке. В ответе укажите V/ π .