Презентация по теме "Решение задач по теме векторы"

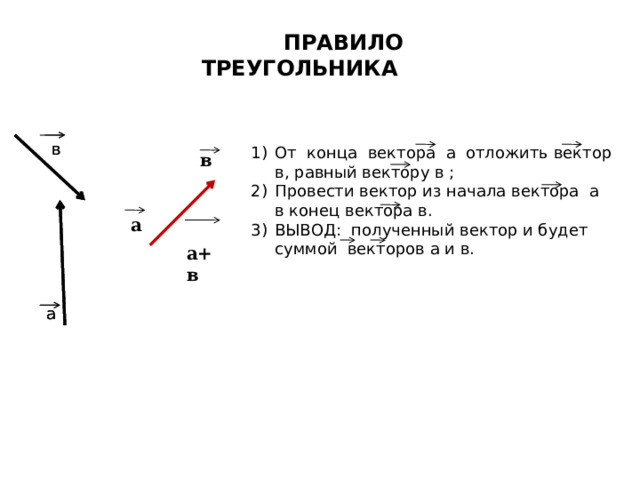
ПРАВИЛО ТРЕУГОЛЬНИКА

в

в

• От конца вектора а отложить вектор в, равный вектору в ;
• Провести вектор из начала вектора а в конец вектора в.
• ВЫВОД: полученный вектор и будет суммой векторов а и в.

в

а+в

а

а

а

а + в

а

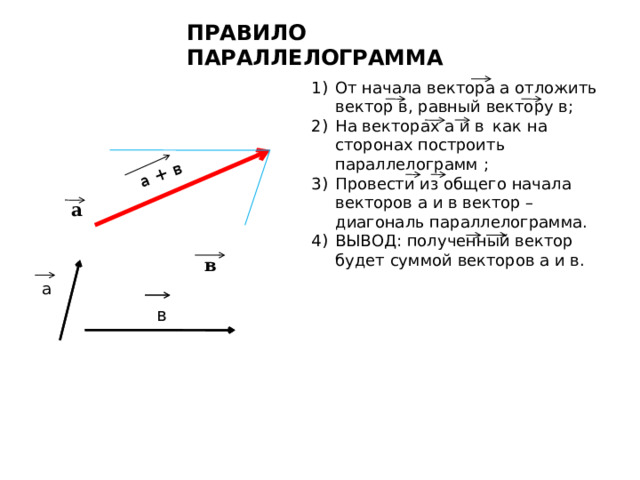
ПРАВИЛО ПАРАЛЛЕЛОГРАММА

• От начала вектора а отложить вектор в, равный вектору в;
• На векторах а и в как на сторонах построить параллелограмм ;
• Провести из общего начала векторов а и в вектор –диагональ параллелограмма.
• ВЫВОД: полученный вектор будет суммой векторов а и в.

а

в

в

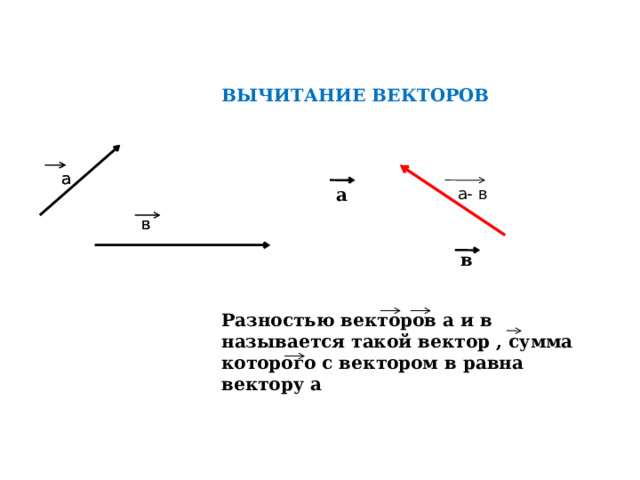
ВЫЧИТАНИЕ ВЕКТОРОВ

а

а

а- в

а

в

в

в

Разностью векторов а и в называется такой вектор , сумма которого с вектором в равна вектору а

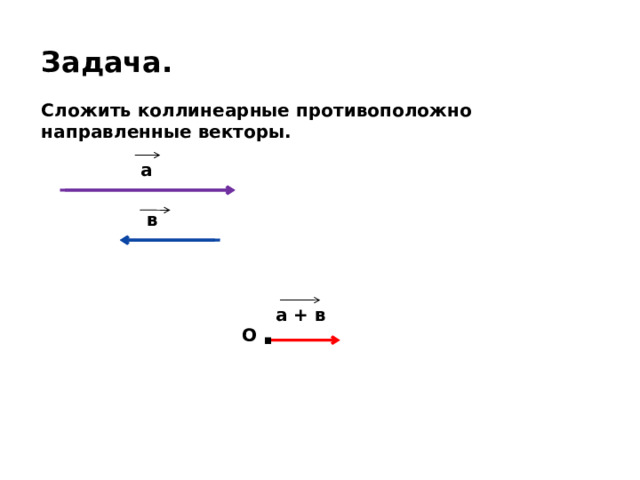
Задача.

Сложить коллинеарные противоположно направленные векторы.

а

в

а + в

.

О

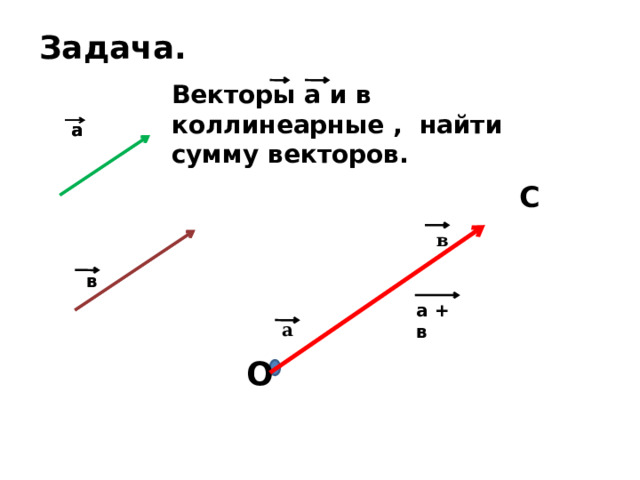
Задача.

Векторы а и в коллинеарные , найти сумму векторов.

а

а

С

в

в

а + в

а

О

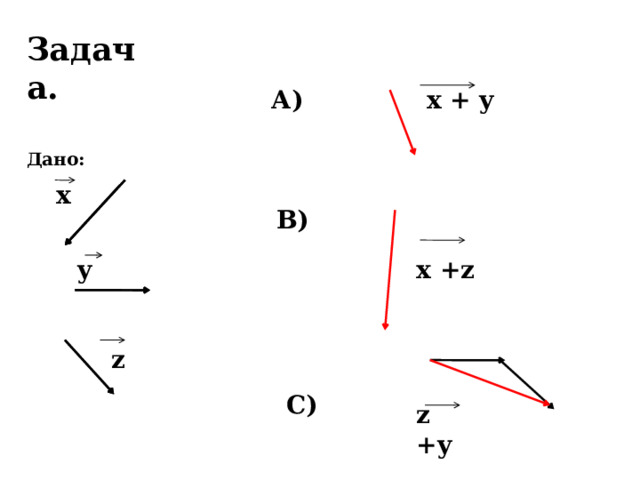
Задача.

Дано:

А)

х + y

х

В)

у

x +z

z

C)

z +y

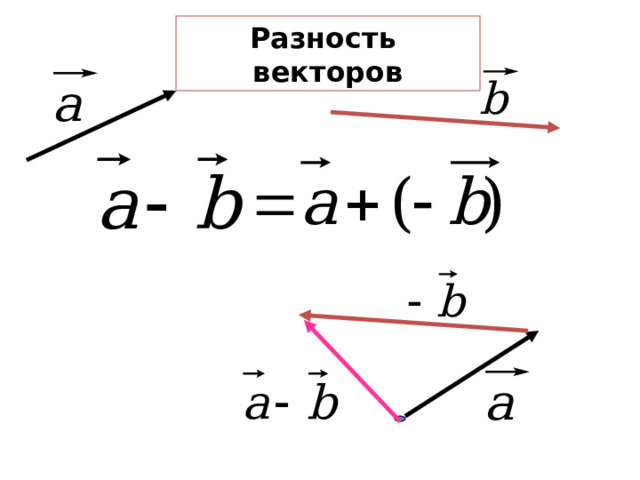
Разность векторов

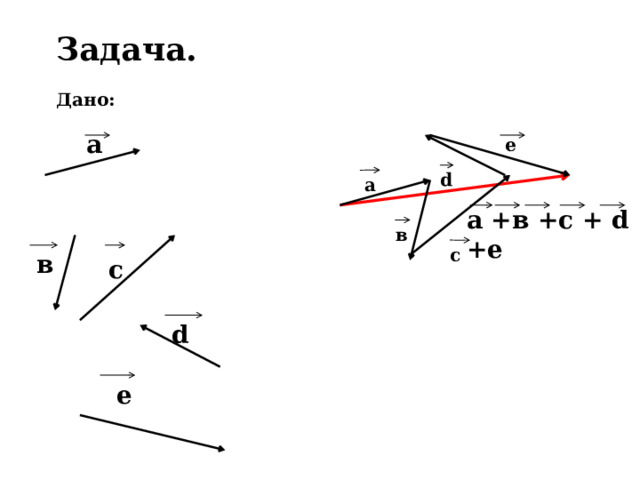
Задача.

Дано:

а

e

d

а

а +в +с + d +е

в

с

в

с

d

е

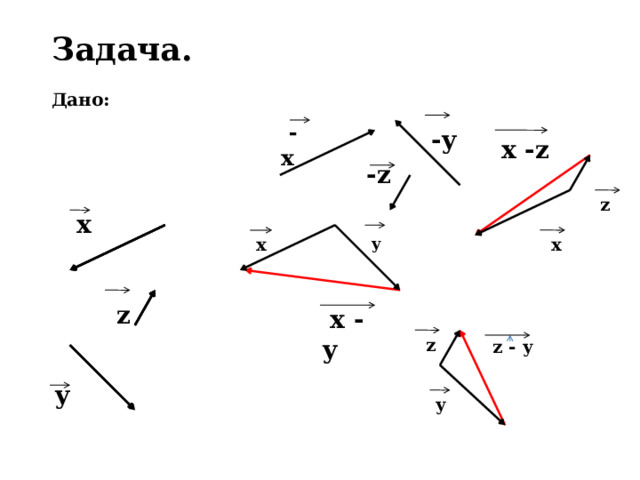
Задача.

Дано:

- х

-y

x -z

-z

z

х

x

x

y

z

х - у

z - y

z

y

у

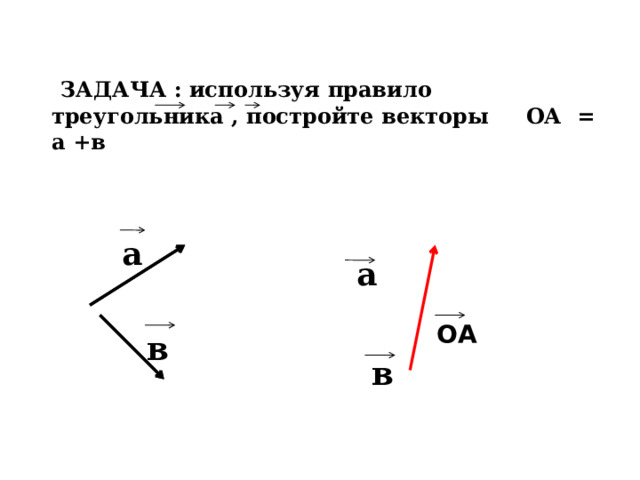
ЗАДАЧА : используя правило треугольника , постройте векторы ОА = а +в

а

а

АА

ОА

в

в

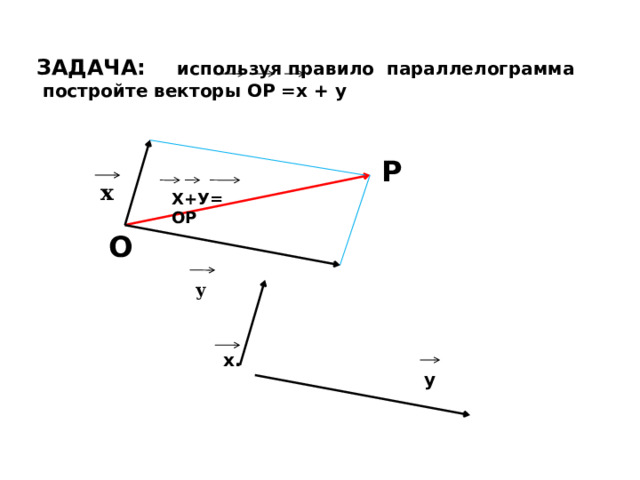
ЗАДАЧА: используя правило параллелограмма

постройте векторы ОР =х + у

P

х

Х+У= ОР

O

у

х.

у

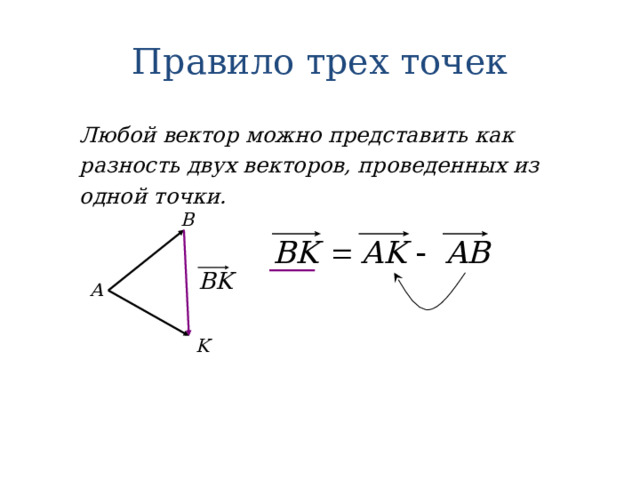
Правило трех точек

Любой вектор можно представить как разность двух векторов, проведенных из одной точки.

B

А

K

Устные вопросы

Справедливо ли утверждение:

а) любые два противоположно направленных вектора коллинеарны?

б) любые два коллинеарных вектора сонаправлены?

в) любые два равных вектора коллинеарны?

г) любые два сонаправленных вектора равны?

д)

е) существуют векторы , и такие, что

и не коллинеарны, и не коллинеарны, а

и коллинеарны?

Ответы

а) ДА

б) НЕТ (могут быть и противоположно направленными)

в) ДА

г) НЕТ (могут иметь разную длину)

д) ДА

е) ДА

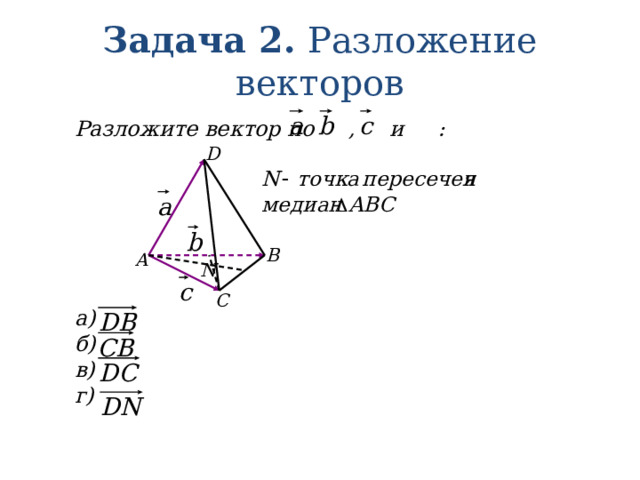
Задача 2. Разложение векторов

Разложите вектор по , и :

а)

б)

в)

г)

D

B

A

N

C

Решение

а)

б)

в)

г)

Задача 3. Сложение и вычитание

Упростите выражения:

а)

б)

в)

г)

д)

е)

Решение

Решение

а)

б)

в)

г)

д)

е)

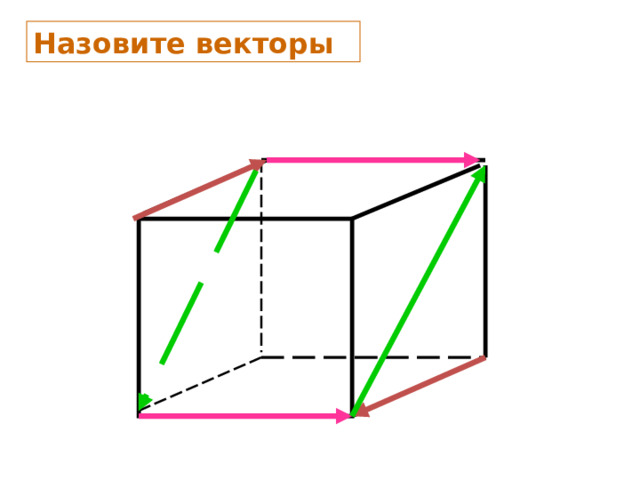
Назовите векторы

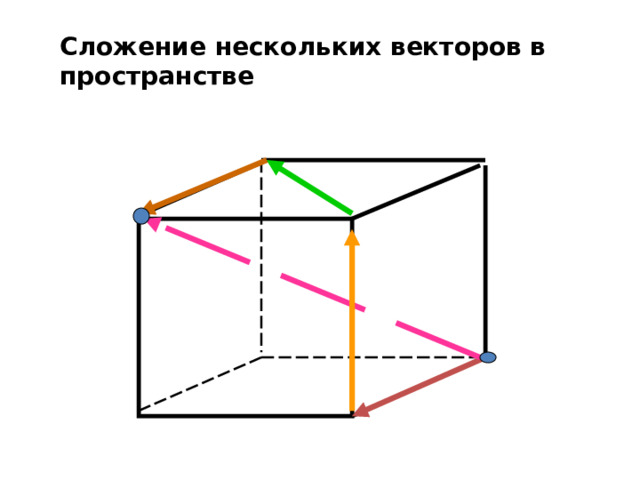
Сложение нескольких векторов в пространстве

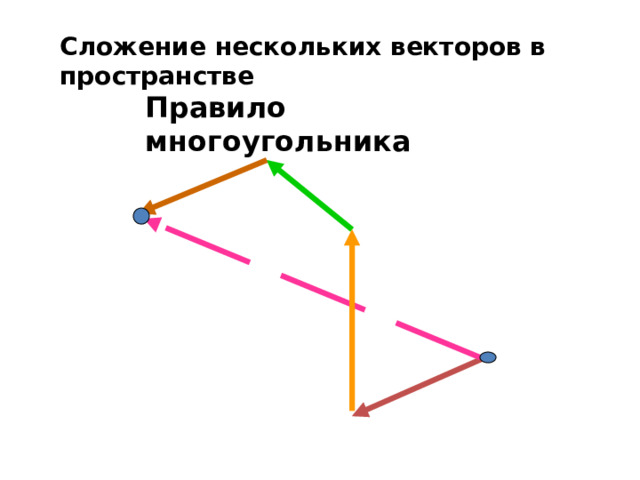
Сложение нескольких векторов в пространстве

Правило многоугольника

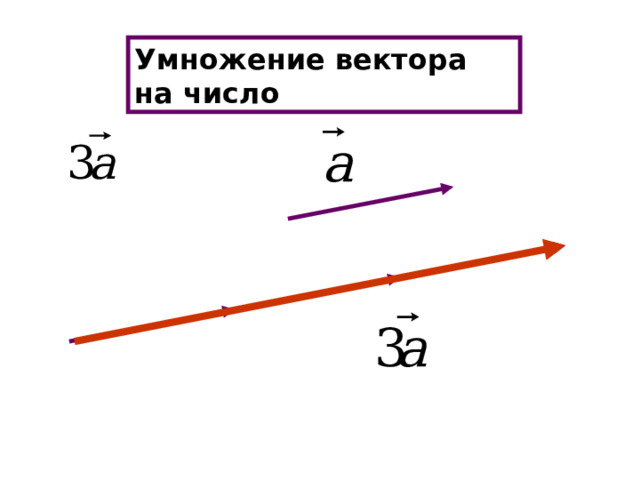
Умножение вектора на число

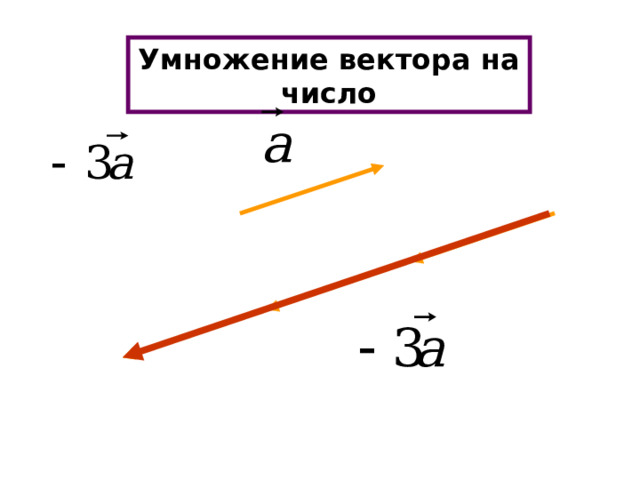
Умножение вектора на число

Умножение вектора на число

Устный тест

1.Что называется вектором?

а)любой отрезок

б)отрезок, обозначенный двумя заглавными латинскими буквами

в) отрезок с выбранным направлением

2. Какой вектор является нулевым?

а)длина вектора равна 0

б)вектор лежит на прямой

в)вектор обозначен одной буквой

3. Векторы коллинеарны, если…

а)лежат на прямых

б)лежат на параллельных прямых

в)один из векторов нулевой

5. Векторы называются равными, если …

а)их длины равны

б)их модули равны и векторы направлены в одну сторону

в)они отложены от одной точки

6. Векторы компланарны, если …

а) они отложены от одной точки

б) они отложены от одной точки и при этом лежат в одной плоскости

в) они лежат в одной плоскости

Упростите выражение

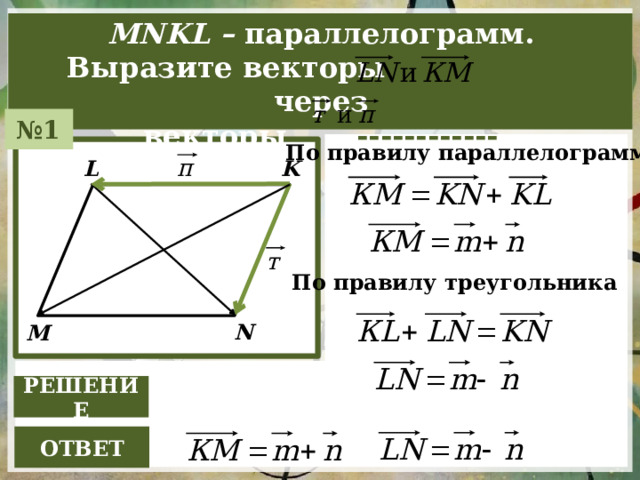
MNKL – параллелограмм.

Bыразите векторы через

векторы ------------

№ 1

По правилу параллелограмма

K

L

По правилу треугольника

N

М

РЕШЕНИЕ

ОТBЕТ

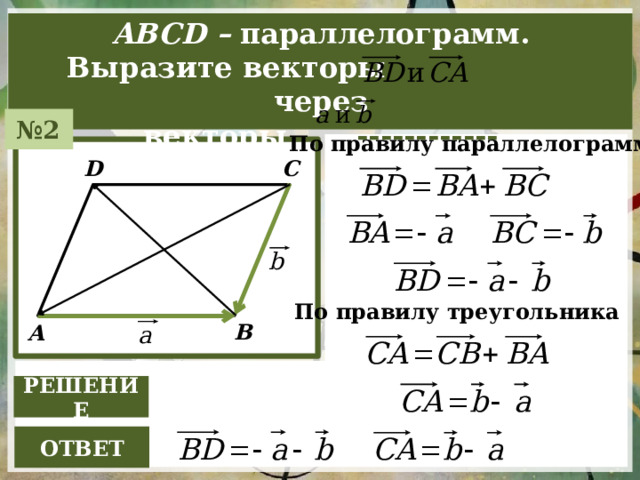
ABCD – параллелограмм.

Bыразите векторы через

векторы ------------

№ 2

По правилу параллелограмма

C

D

По правилу треугольника

B

A

РЕШЕНИЕ

ОТBЕТ

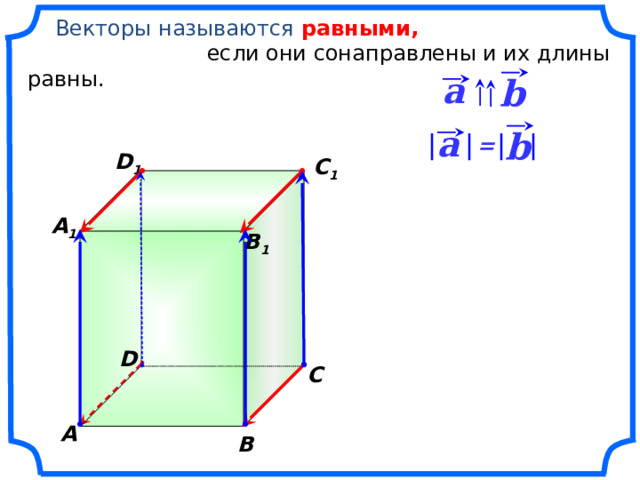
Векторы называются равными,

если они сонаправлены и их длины равны.

a

b

a

b

=

D 1

C 1

A 1

B 1

«Геометрия 10-11» Л.С. Атанасян и др. Рисунки Савченко Е.М.

D

C

A

B

29

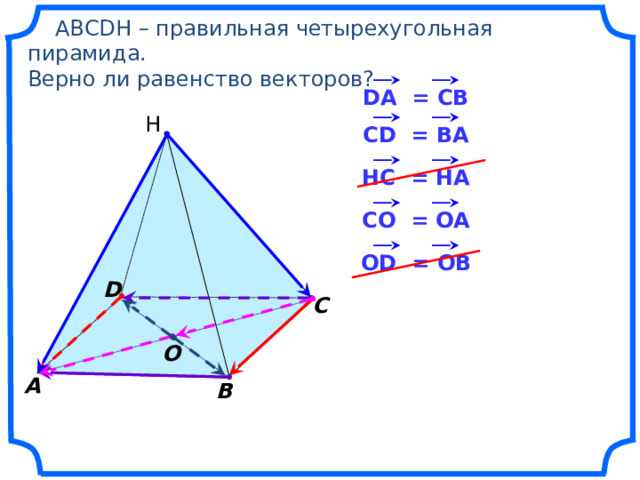
АВСDH – правильная четырехугольная пирамида.

Верно ли равенство векторов?

DA = CB

Н

CD = BA

HC = HA

CO = OA

OD = OB

D

С

O

А

В

30

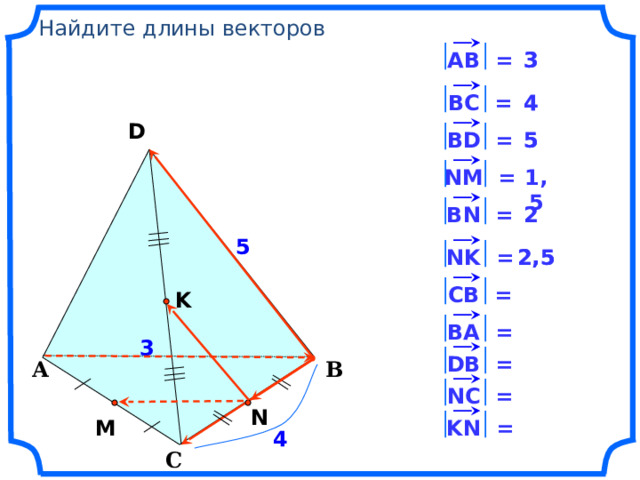
Найдите длины векторов

3

АВ =

3

4

4

ВC =

D

5

S

ВD =

5

1,5

NM =

2

2

BN =

5

2,5

NK =

2,5

CB =

K

«Геометрия 10-11» Л.С. Атанасян и др.

BA =

3

DB =

А

В

NC =

N

M

KN =

4

С

31