Российская Федерация, Москва
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до 24.05.2025
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 20.05.2025 23:40
Егорова Татьяна Савельевна
Учитель математики
60 лет
6 575
7 413 
Местоположение
Специализация
Презентация по теме "Взаимное расположение прямой и окружности"
Категория:
Математика
17.04.2023 23:53
Просмотр содержимого документа
«Презентация по теме "Взаимное расположение прямой и окружности"»
ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ И ОКРУЖНОСТИ
Как вы думаете, сколько общих точек могут иметь прямая и окружность?
О
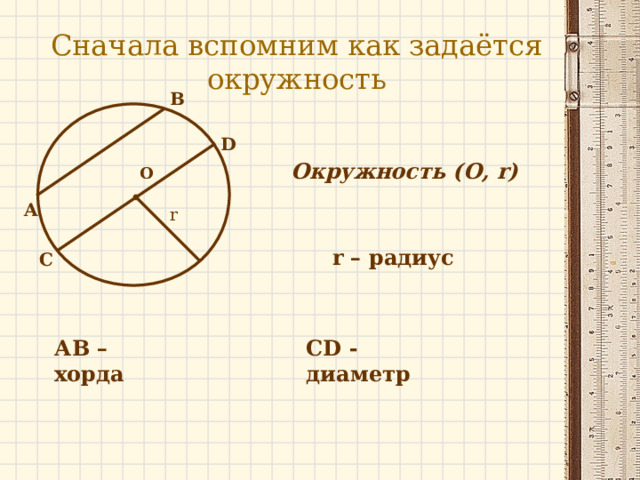
Сначала вспомним как задаётся окружность
B
D
Окружность (О, r )
О
A
r
r – радиус
С
АВ – хорда
CD - диаметр
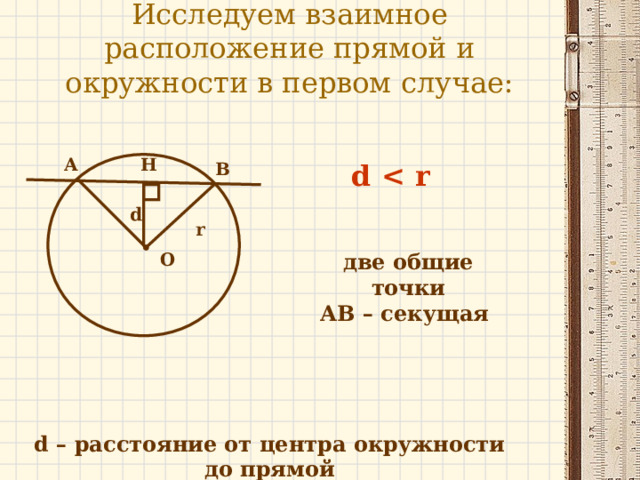
Исследуем взаимное расположение прямой и окружности в первом случае:
Н
А
В
d
d
r
О
две общие точки
АВ – секущая
d – расстояние от центра окружности до прямой
Второй случай:
d = r
одна общая точка
Н
d
r
О
d – расстояние от центра окружности до прямой
r d r не имеют общих точек О d – расстояние от центра окружности до прямой " width="640"
Третий случай:
H
d r
d
r
не имеют общих точек
О
d – расстояние от центра окружности до прямой
r две общие точки одна общая точка не имеют общих точек Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют только одну общую точку . Если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая и окружность имеют две общие точки . Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек . " width="640"
Сколько общих точек могут иметь прямая и окружность?
d
d = r
d r
две общие точки
одна общая точка
не имеют общих точек
Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют только одну общую точку .
Если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая и окружность имеют две общие точки .
Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек .
Касательная к окружности
Определение: П рямая, имеющая с окружностью только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.
M
m
s = r
O
Свойство касательной: Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
M
m – касательная к окружности с центром О
М – точка касания
OM - радиус
m
O
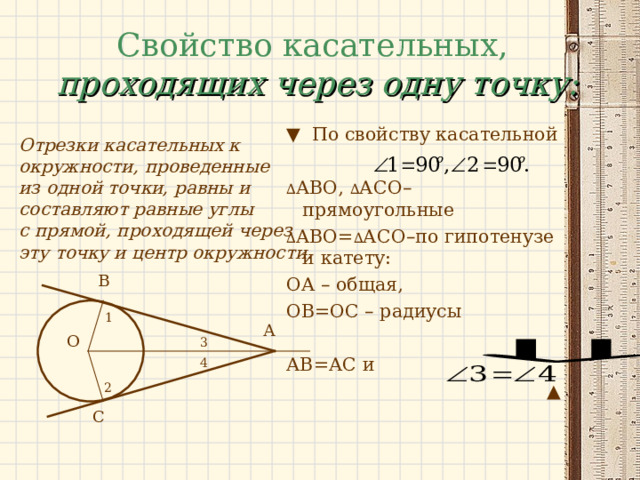
Свойство касательных, проходящих через одну точку:
Отрезки касательных к
окружности, проведенные
из одной точки, равны и
составляют равные углы
с прямой, проходящей через
эту точку и центр окружности.
▼ По свойству касательной
∆ АВО, ∆ АСО–прямоугольные
∆ АВО= ∆ АСО–по гипотенузе и катету:
ОА – общая,
ОВ=ОС – радиусы
АВ=АС и
▲
В
1
А
О
3
4
2
С
Признак касательной: Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна радиусу, то она является к асательной.
M
m
окружность с центром О
радиуса OM
m – прямая, которая проходит через точку М
и
m – касательная
O
© 2023, Егорова Татьяна Савельевна 499 20
Рекомендуем курсы ПК и ППК для учителей
Похожие файлы
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
Полезное для учителя
Реализация образовательных программ осуществляется с применением исключительно электронного обучения и ДОТ
Закрыть через 5 секунд
