Презентация «Правильные многогранники»

БПОУ ВО «Воронежский государственный промышленно-гуманитарный колледж им. В.М. Пескова»

Правильные многогранники (справочные материалы)

Разработчик: Н.Л.Латышева

«Многогранники – фигуры особого очарования с богатой родословной» Клауди Альсина, испанский математик, профессор.

Призма

Антипризма

Пирамида

Параллелепипед

Усеченная пирамида

Тела Кеплера-Пуансо

Тела Архимеда

Тела Платона

Каталановы тела

Соединения многогранников

Другие звездчатые многогранники

выпуклые

Чтобы понять, является ли многогранник выпуклым , можно:

• … рассмотреть отрезки, соединяющие точки, расположенные внутри его или на его гранях, и проверить, находятся ли эти отрезки полностью внутри многогранника;
• … проверить, будет ли многогранник целиком располагаться по одну сторону от плоскости каждой из его граней;
• … показать, что сечение многогранника произвольной плоскостью является выпуклым многоугольником. Пуансо

Правильные

Выпуклый многогранник называется  правильным , если его гранями являются равные правильные многоугольники и в каждой вершине сходится одинаковое число граней.

Тела Платона

Выпуклые правильные многогранники принято называть Платоновыми телами, хотя они были известны задолго до Платона.

Платон определяет правильный многогранник так: «имеющий свойство делить всю описанную около него сферу на равные и подобные части».

Платон отождествляет многогранники с прекрасным, однако эта красота у него связана не с их геометрической формой, а с воплощенными в ней математическими свойствами: «… тела, прекраснейшие из всех, которые не подобны друг другу, однако способны, разрушаясь друг в друга перерождаться».

Платон  (427–347 до н.э.) – великий древнегреческий философ, ученик Сократа, основатель Академии.

Платон в своих трудах сумел обобщить многие, существующие в его эпоху, разрозненные философские и математические знания Востока и Запада об элементарных началах бытия и творения Жизни. Главная заслуга Платона в истории математики заключается в том, что он под влиянием пифагорейцев, в противовес своему учителю Сократу и софистам, которые не считали нужным для философов изучать математику, признавал, что знание математики необходимо каждому образованному человеку. На дверях его академии была надпись: "Пусть тот, кто не знает геометрии, не входит сюда".

Вклад Платона в математику незначителен. Однако его идеи относительно структуры и методов математики чрезвычайно ценны. Он ввел традицию давать безукоризненные определения и определять, какие положения в математических соображениях можно принимать без доказательства. Платон ввел термины "анализ" и "синтез", первым обосновал метод доказательства от противного, который теперь широко применяется в геометрии. В школе Платона особое внимание уделялось решению задач на построение. Благодарю этому в ней сформировалось понятие о геометрическом месте точек, а также была разработана методика решения задач на построение. Заслуга Платона и в том, что он не разрешал использовать при построении никаких приспособлений, кроме циркуля и линейки. Это ограничение имело большое значение для развития геометрии. 

Уместно было бы упомянуть Платона под его собственным именем – Аристокл, т.к. Платон – это прозвище, которое означает «широкоплечий».

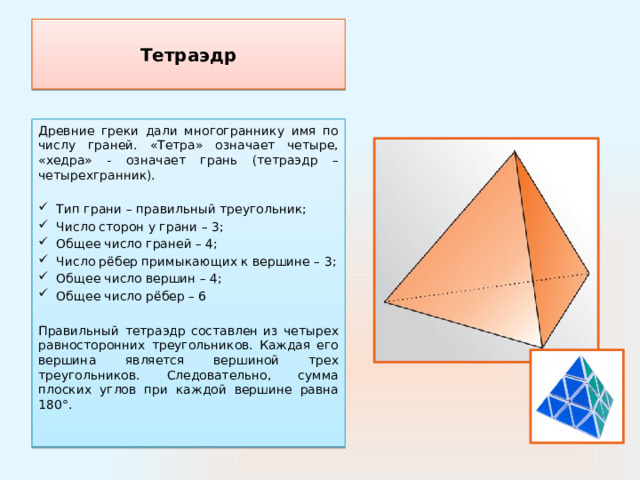
Тетраэдр

Древние греки дали многограннику имя по числу граней. «Тетра» означает четыре, «хедра» - означает грань (тетраэдр – четырехгранник). 

• Тип грани – правильный треугольник;
• Число сторон у грани – 3;
• Общее число граней – 4;
• Число рёбер примыкающих к вершине – 3;
• Общее число вершин – 4;
• Общее число рёбер – 6

Правильный тетраэдр составлен из четырех равносторонних треугольников. Каждая его вершина является вершиной трех треугольников. Следовательно, сумма плоских углов при каждой вершине равна 180°.

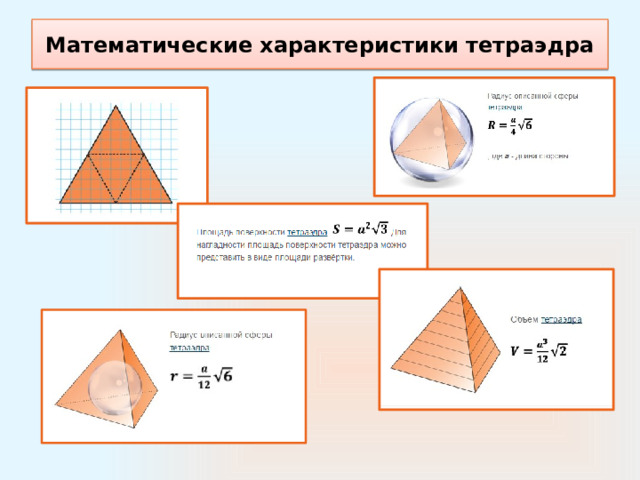
Математические характеристики тетраэдра

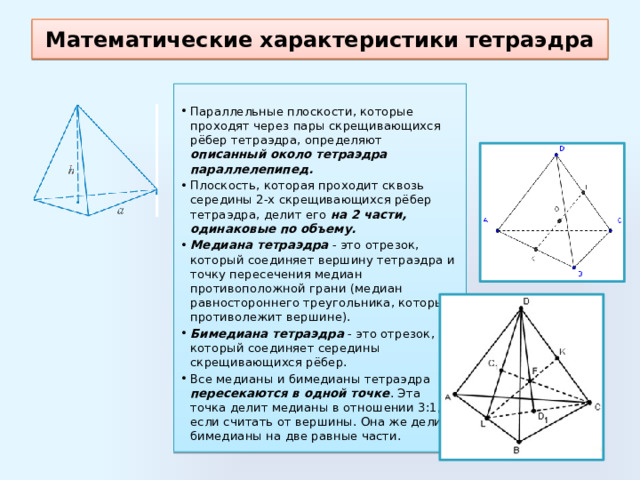
Математические характеристики тетраэдра

• Параллельные плоскости, которые проходят через пары скрещивающихся рёбер тетраэдра, определяют описанный около тетраэдра параллелепипед.
• Плоскость, которая проходит сквозь середины 2-х скрещивающихся рёбер тетраэдра, делит его на 2 части, одинаковые по объему.
• Медиана тетраэдра  - это отрезок, который соединяет вершину тетраэдра и точку пересечения медиан противоположной грани (медиан равностороннего треугольника, который противолежит вершине).
• Бимедиана тетраэдра  - это отрезок, который соединяет середины скрещивающихся рёбер.
• Все медианы и бимедианы тетраэдра пересекаются в одной точке . Эта точка делит медианы в отношении 3:1, если считать от вершины. Она же делит бимедианы на две равные части.

Октаэдр

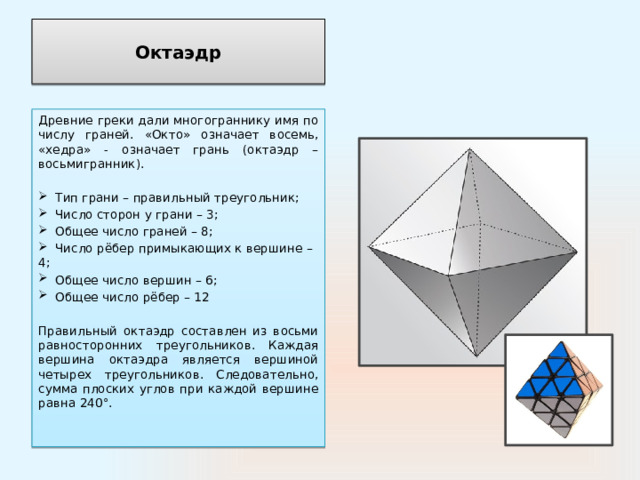
Древние греки дали многограннику имя по числу граней. «Окто» означает восемь, «хедра» - означает грань (октаэдр – восьмигранник). 

• Тип грани – правильный треугольник;
• Число сторон у грани – 3;
• Общее число граней – 8;
• Число рёбер примыкающих к вершине – 4;
• Общее число вершин – 6;
• Общее число рёбер – 12

Правильный октаэдр составлен из восьми равносторонних треугольников. Каждая вершина октаэдра является вершиной четырех треугольников. Следовательно, сумма плоских углов при каждой вершине равна 240°.

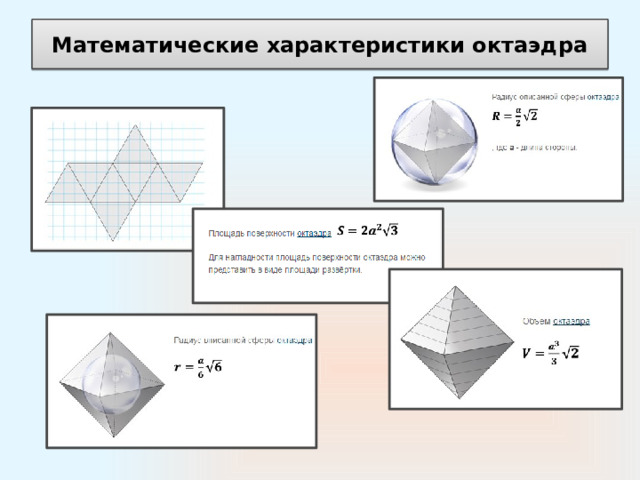
Математические характеристики октаэдра

Математические характеристики октаэдра

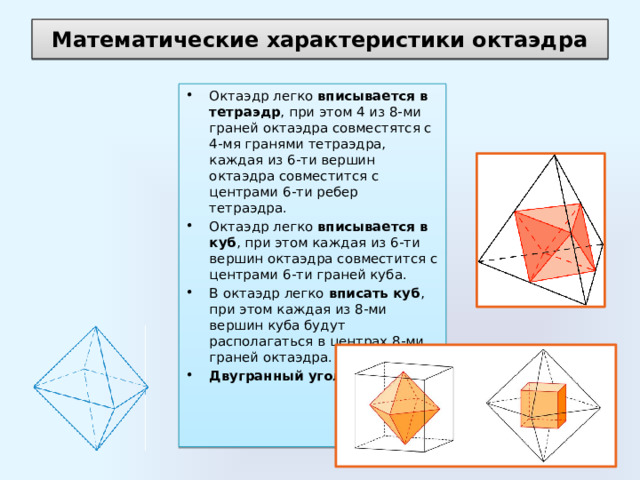
• Октаэдр легко вписывается в тетраэдр , при этом 4 из 8-ми граней октаэдра совместятся с 4-мя гранями тетраэдра, каждая из 6-ти вершин октаэдра совместится с центрами 6-ти ребер тетраэдра.
• Октаэдр легко вписывается в куб , при этом каждая из 6-ти вершин октаэдра совместится с центрами 6-ти граней куба.
• В октаэдр легко вписать куб , при этом каждая из 8-ми вершин куба будут располагаться в центрах 8-ми граней октаэдра.
• Двугранный угол :  α≈109,47°  .

Икосаэдр

Древние греки дали многограннику имя по числу граней. «Икоси» означает двадцать, «хедра» - означает грань (Икосаэдр – двадцатигранник). 

• Тип грани – правильный треугольник;
• Число сторон у грани – 3;
• Общее число граней – 20;
• Число рёбер примыкающих к вершине – 5;
• Общее число вершин – 12;
• Общее число рёбер – 30;

Правильный икосаэдр составлен из двадцати равносторонних треугольников. Каждая вершина икосаэдра является вершиной пяти треугольников. Следовательно, сумма плоских углов при каждой вершине равна 300°.

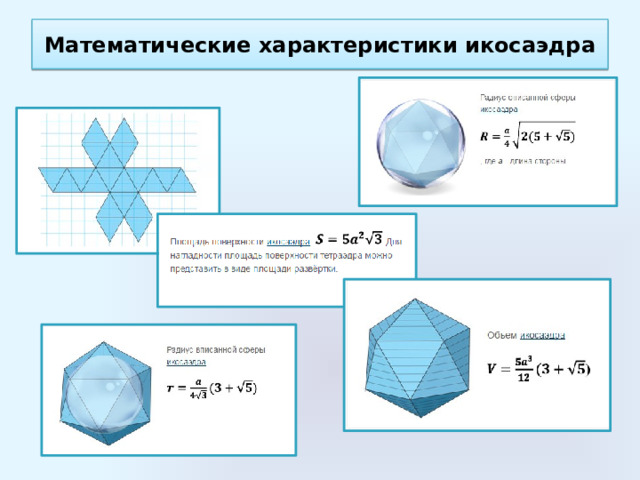
Математические характеристики икосаэдра

Математические характеристики икосаэдра

• Каждая из 12 вершин икосаэдра лежит по 3 в 4-х параллельных плоскостях , образуя во всех плоскостях правильный треугольник.
• 10 вершин икосаэдра находятся в 2-х параллельных плоскостях, и образуют в них 2 правильных 5-ти угольника, а оставшиеся 2 — противоположны друг другу и находятся в 2-х концах диаметра описанной вокруг икосаэдра сферы, который перпендикулярен параллельным плоскостям.
• В икосаэдр можно вписать тетраэдр , таким образом, чтобы 4 вершины тетраэдра станут совмещены с 4-мя вершинами икосаэдра.
• Сделать икосаэдр можно из 20 тетраэдров . Нельзя сделать икосаэдр из правильных тетраэдров, потому что радиус описанной сферы вокруг икосаэдра и длина бокового ребра тетраэдра меньше ребра икосаэдра.
• Октаэдр можно вписать в икосаэдр так, что вершинами октаэдра будут середины ребер икосаэдра.  Икосаэдр можно вписать в октаэдр так, что центрами граней икосаэдра будут центры граней октаэдра.

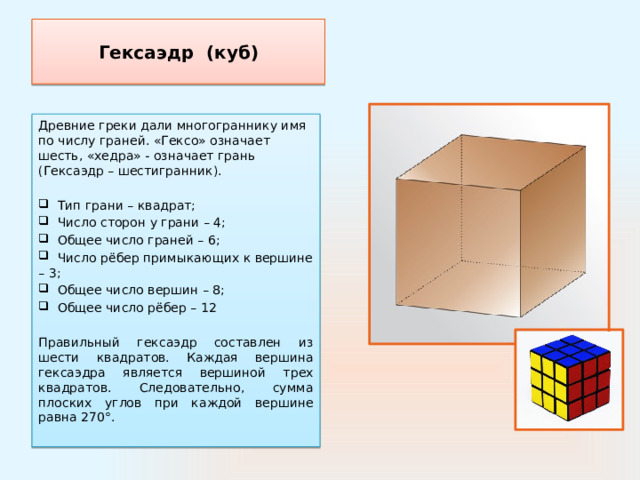
Гексаэдр (куб)

Древние греки дали многограннику имя по числу граней. «Гексо» означает шесть, «хедра» - означает грань (Гексаэдр – шестигранник). 

• Тип грани – квадрат;
• Число сторон у грани – 4;
• Общее число граней – 6;
• Число рёбер примыкающих к вершине – 3;
• Общее число вершин – 8;
• Общее число рёбер – 12

Правильный гексаэдр составлен из шести квадратов. Каждая вершина гексаэдра является вершиной трех квадратов. Следовательно, сумма плоских углов при каждой вершине равна 270°.

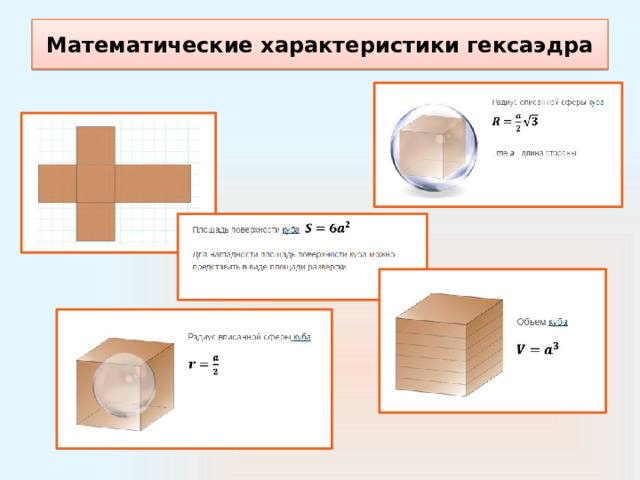
Математические характеристики гексаэдра

Математические характеристики куба

• 4 сечения куба имеют вид правильных шестиугольников — они проходят сквозь центр куба перпендикулярно четырём его главным диагоналям.
• В куб вписывают тетраэдр  2-мя способами. В любом из них 4 вершины тетраэдра всегда совмещены с 4-мя вершинами куба и каждое из шести ребер тетраэдра принадлежат граням куба.
• В 1-м случае каждая вершина тетраэдра принадлежит граням трехгранного угла, вершиной совпадающего с одной из вершин куба.
• Во 2-м случае ребра тетраэдра, которые попарно скрещиваются принадлежат попарно противоположным граням куба. Такой тетраэдр будет правильным, а его объём будет составлять треть от объёма куба.
• В куб вписывают икосаэдр , притом 6 взаимно параллельных рёбер икосаэдра располагаются на 6-ти гранях куба, следующие 24 ребра располагаются внутри куба. Каждая из 12 вершин икосаэдра располагается на 6-ти гранях куба.

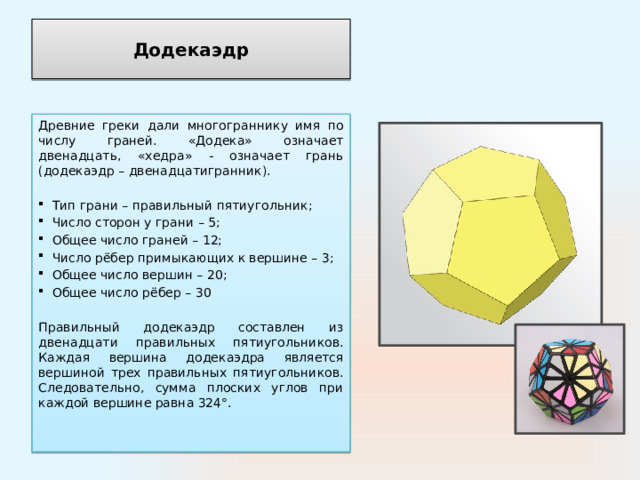
Додекаэдр

Древние греки дали многограннику имя по числу граней. «Додека» означает двенадцать, «хедра» - означает грань (додекаэдр – двенадцатигранник). 

• Тип грани – правильный пятиугольник;
• Число сторон у грани – 5;
• Общее число граней – 12;
• Число рёбер примыкающих к вершине – 3;
• Общее число вершин – 20;
• Общее число рёбер – 30

Правильный додекаэдр составлен из двенадцати правильных пятиугольников. Каждая вершина додекаэдра является вершиной трех правильных пятиугольников. Следовательно, сумма плоских углов при каждой вершине равна 324°.

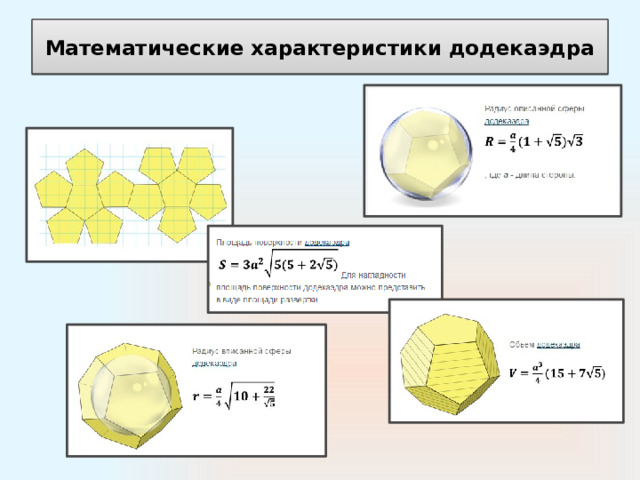
Математические характеристики додекаэдра

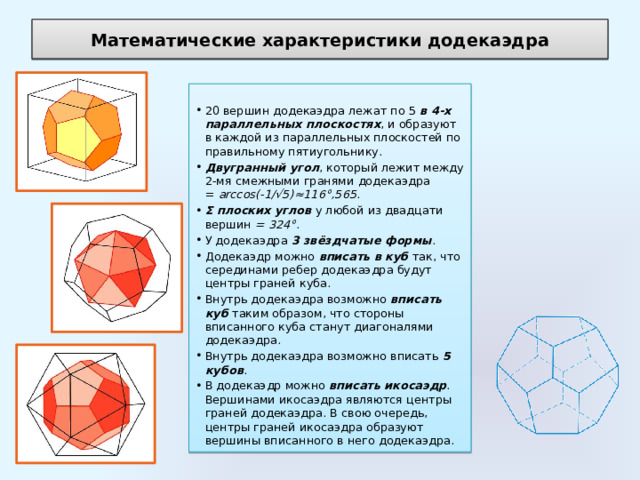
Математические характеристики додекаэдра

• 20 вершин додекаэдра лежат по 5 в 4-х параллельных плоскостях , и образуют в каждой из параллельных плоскостей по правильному пятиугольнику.
• Двугранный угол , который лежит между 2-мя смежными гранями додекаэдра =  arccos(-1/√5)≈116°,565 .
• Ʃ плоских углов у любой из двадцати вершин  = 324° .
• У додекаэдра 3 звёздчатые формы .
• Додекаэдр можно вписать в куб так, что серединами ребер додекаэдра будут центры граней куба. 
• Внутрь додекаэдра возможно вписать куб таким образом, что стороны вписанного куба станут диагоналями додекаэдра.
• Внутрь додекаэдра возможно вписать 5 кубов .
• В додекаэдр можно вписать икосаэдр . Вершинами икосаэдра являются центры граней додекаэдра. В свою очередь, центры граней икосаэдра образуют вершины вписанного в него додекаэдра. 

Симметрия правильных многогранников

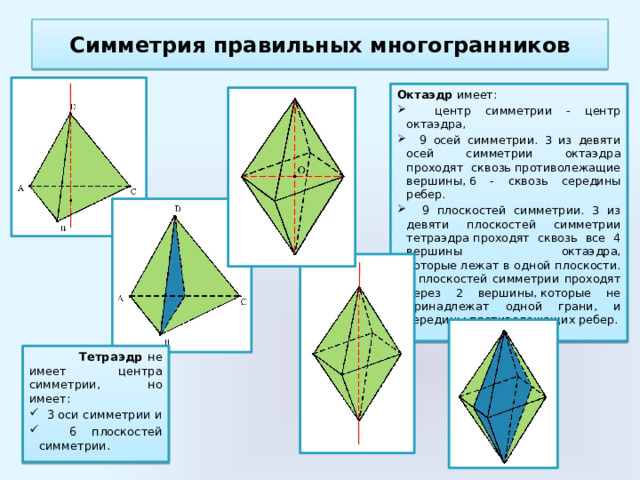
Октаэдр имеет:

• центр симметрии - центр октаэдра,
• 9 осей симметрии. 3 из девяти осей симметрии октаэдра проходят сквозь противолежащие вершины, 6 - сквозь середины ребер.
• 9 плоскостей симметрии. 3 из девяти плоскостей симметрии тетраэдра проходят сквозь все 4 вершины октаэдра, которые лежат в одной плоскости. 6 плоскостей симметрии проходят через 2 вершины, которые не принадлежат одной грани, и середины противолежащих ребер.

Тетраэдр не имеет центра симметрии, но имеет:

• 3 оси симметрии и
• 6 плоскостей симметрии.

Симметрия правильных многогранников

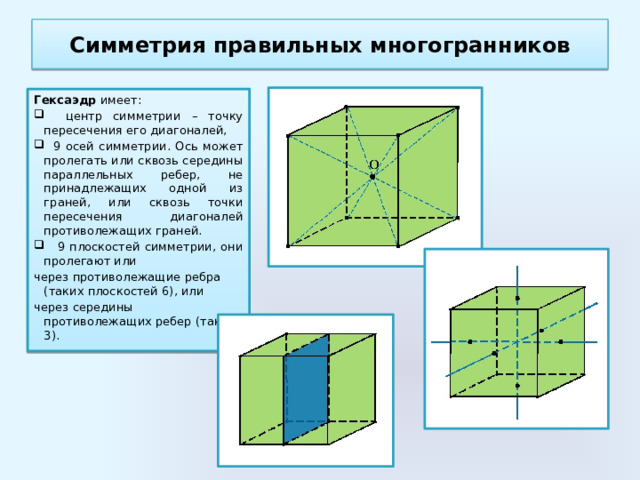
Гексаэдр имеет:

• центр симметрии – точку пересечения его диагоналей,
• 9 осей симметрии. Ось может пролегать или сквозь середины параллельных ребер, не принадлежащих одной из граней, или сквозь точки пересечения диагоналей противолежащих граней.
• 9 плоскостей симметрии, они пролегают или

через противолежащие ребра (таких плоскостей 6), или

через середины противолежащих ребер (таких 3).

Симметрия правильных многогранников

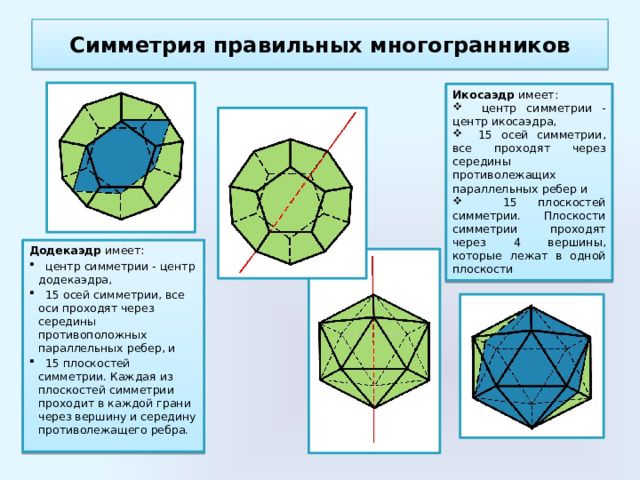
Икосаэдр имеет:

• центр симметрии - центр икосаэдра,
• 15 осей симметрии, все проходят через середины противолежащих параллельных ребер и
• 15 плоскостей симметрии. Плоскости симметрии проходят через 4 вершины, которые лежат в одной плоскости

Додекаэдр имеет:

• центр симметрии - центр додекаэдра,
• 15 осей симметрии, все оси проходят через середины противоположных параллельных ребер, и
• 15 плоскостей симметрии. Каждая из плоскостей симметрии проходит в каждой грани через вершину и середину противолежащего ребра.

Двойственность правильных многогранников

Рассмотрим произвольный выпуклый многогранник и возьмём точки в серединах его граней.

Соединим между собой точки соседних граней отрезками. Тогда точки являются вершинами, отрезки — рёбрами, а многоугольники, которые ограничивают эти отрезки, гранями ещё одного выпуклого многогранника.

Этот многогранник называется двойственным к исходному.

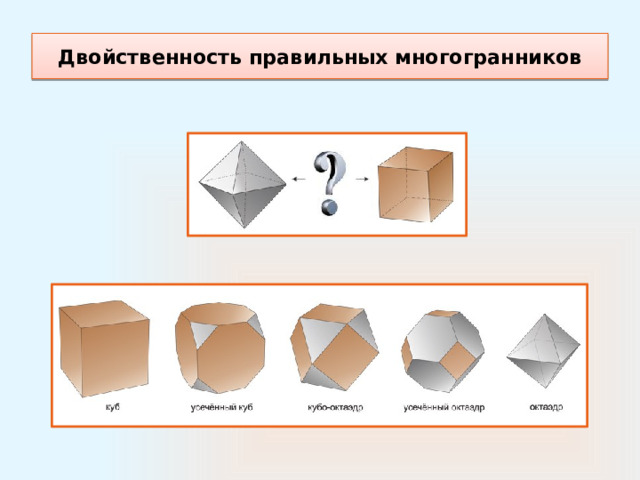
Двойственность правильных многогранников

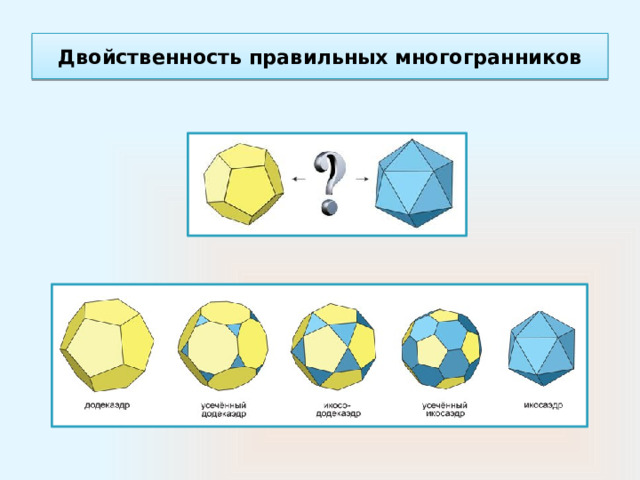
Двойственность правильных многогранников

Правильные многогранники известны с древнейших времён.

Их орнаментные модели можно найти на резных каменных шарах, созданных в период позднего неолита, в Шотландии, как минимум за 1000 лет до Платона. В костях, которыми люди играли на заре цивилизации, уже угадываются формы правильных многогранников.

В значительной мере правильные многогранники были изучены древними греками. Некоторые источники (такие как Прокл Диадох) приписывают честь их открытия Пифагору . Другие утверждают, что ему были знакомы только тетраэдр, куб и додекаэдр, а честь открытия октаэдра и икосаэдра принадлежит Теэтету Афинскому , современнику Платона. В любом случае, Теэтет дал математическое описание всем пяти правильным многогранникам   и первое известное доказательство того, что их ровно пять.

Пифагор

Теэтет

Правильные многогранники характерны для философии Платона,

в честь которого и получили название «Платоновы тела». Платон писал о них в своём трактате Тимей (360г до н. э.), где сопоставил каждую из четырёх стихий (землю, воздух, воду и огонь) определённому правильному многограннику.

Земля сопоставлялась кубу, воздух — октаэдру, вода — икосаэдру, а огонь — тетраэдру. Для возникновения данных ассоциаций были следующие причины: жар огня ощущается чётко и остро (как маленькие тетраэдры); воздух состоит из октаэдров: его мельчайшие компоненты настолько гладкие, что их с трудом можно почувствовать; вода выливается, если её взять в руку, как будто она сделана из множества маленьких шариков (к которым ближе всего икосаэдры); в противоположность воде, совершенно непохожие на шар кубики составляют землю, что служит причиной тому, что земля рассыпается в руках, в противоположность плавному току воды.

По поводу пятого элемента, додекаэдра, Платон сделал смутное замечание: «…его бог определил для Вселенной и прибегнул к нему в качестве образца». Аристотель добавил пятый элемент — эфир и постулировал, что небеса сделаны из этого элемента, но он не сопоставлял его платоновскому пятому элементу.

Евклид (умер между 275 и 270 до н. э.), древнегреческий математик.

Работал в Александрии в 3 в. до н. э. Главный труд "Начала" (15 книг), содержащий основы античной математики, элементарной геометрии и теории чисел, оказал огромное влияние на развитие математики. 

Евклид:

• Дал полное математическое описание правильных многогранников в последней, XIII книге Начал. Предложения 13—17 этой книги описывают структуру тетраэдра, октаэдра, куба, икосаэдра и додекаэдра в данном порядке.
• Для каждого многогранника Евклид нашёл отношение диаметра описанной сферы к длине ребра.
• В 18-м предложении утверждается, что не существует других правильных многогранников.

Большое количество информации XIII книги «Начал», возможно, взято из трудов Теэтета.

Иоганн Кеплер (1571—1630) в своей работе «Тайна мироздания» в 1596 году,

используя правильные многогранники, вывел принцип, которому подчиняются формы и размеры орбит планет Солнечной системы. От внутренних планет к внешним период обращения планет возрастал пропорционально удвоенной разницы радиусов сфер.

Геометрия Солнечной системы, по Кеплеру, заключалась в следующем:

• « Земля (имеется в виду орбита Земли) есть мера всех орбит.
• Вокруг нее опишем додекаэдр.
• Описанная вокруг додекаэдра сфера есть сфера Марса .
• Вокруг сферы Марса опишем тетраэдр .
• Описанная вокруг тетраэдра сфера есть сфер Юпитера .
• Вокруг сферы Юпитера опишем куб .
• Описанная вокруг куба сфера есть сфера Сатурна .
• В сферу Земли вложим икосаэдр .
• Вписанная в нег сфера есть сфера Венеры .
• В сферу Венеры вложим октаэдр .
• Вписанная него сфера есть сфера Меркурия ».

Такая модель Солнечной системы получила название «Космического кубка» Кеплера.

Позже от оригинальной идеи Кеплера пришлось отказаться, но результатом его поисков стало открытие двух законов орбитальной динамики —  законов Кеплера , — изменивших курс физики и астрономии, а также правильных звёздчатых многогранников ( тел Кеплера-Пуансо ).

Тела Кеплера-пуансо

Красивые формы имеют так называемые звездчатые многогранники, то есть правильные невыпуклые многогранники. Они получаются из правильных многогранников продолжением их граней или ребер. Их всего четыре. Первые два были открыты И. Кеплером, а два других почти 200 лет спустя построил Л. Пуансо (1777—1859). В 1811 году французский математик О. Коши (1789-1857) в работе «Исследование о многогранниках» доказал, что других правильных звездчатых многогранников не существует. 

Малый звездчатый додекаэдр 

Из тетраэдра, куба и октаэдра правильные звездчатые многогранники не получаются. 

Возьмем додекаэдр. Продолжение его ребер приводит к замене каждой грани звездчатым правильным пятиугольником (пятиконечной звездой), и в результате возникает многогранник, который называется  малым звездчатым додекаэдром .

У малого звёздчатого додекаэдра грани - пятиконечные звёзды (пентаграммы), которые сходятся по 5 в каждой вершине. 

Малый звёздчатый додекаэдр имеет следующие характеристики:

• 12 пятигранных пирамид, основанием которых является додекаэдр
• Грани: – 60 треугольников
• Вершины: - 12
• Ребра – 90.

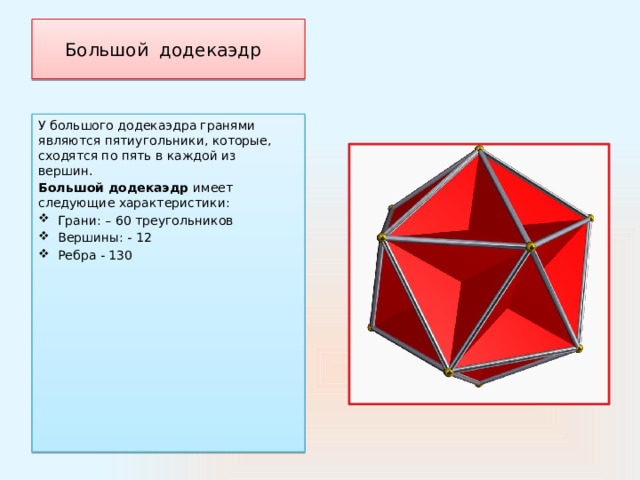
Большой  додекаэдр  

У большого додекаэдра гранями являются пятиугольники, которые, сходятся по пять в каждой из вершин. 

Большой додекаэдр имеет следующие характеристики:

• Грани: – 60 треугольников
• Вершины: - 12
• Ребра - 130

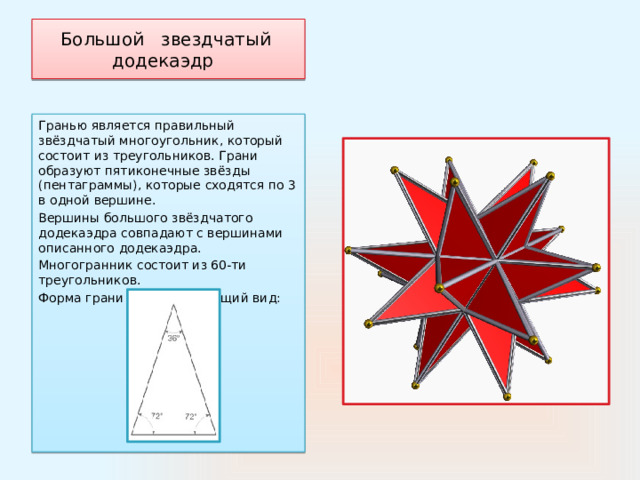
Большой   звездчатый  додекаэдр  

Гранью является правильный звёздчатый многоугольник, который состоит из треугольников. Грани образуют пятиконечные звёзды (пентаграммы), которые сходятся по 3 в одной вершине. 

Вершины большого звёздчатого додекаэдра совпадают с вершинами описанного додекаэдра.

Многогранник состоит из 60-ти треугольников.

Форма грани имеет следующий вид:

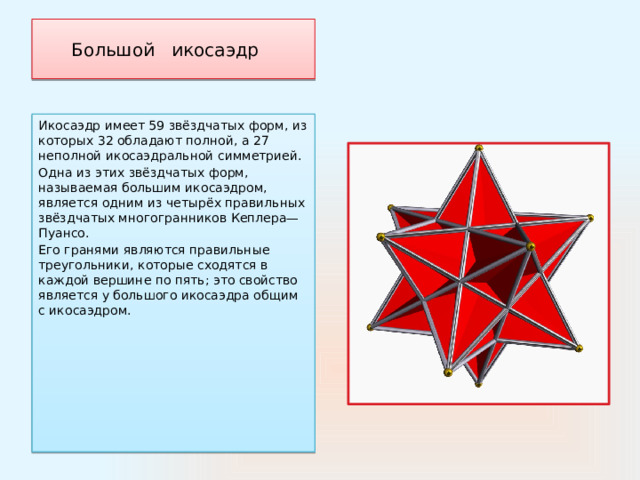
Большой   икосаэдр   

Икосаэдр имеет 59 звёздчатых форм, из которых 32 обладают полной, а 27 неполной икосаэдральной симметрией.

Одна из этих звёздчатых форм, называемая большим икосаэдром, является одним из четырёх правильных звёздчатых многогранников Кеплера—Пуансо.

Его гранями являются правильные треугольники, которые сходятся в каждой вершине по пять; это свойство является у большого икосаэдра общим с икосаэдром.

«Главная причина, по которой изучают правильные многогранники, не изменилась со времен Пифагора и заключается в том, что эти многогранники кажутся нам привлекательными» Гарольд Коксетер, канадский математик (1907 - 2003)

Источники: Мир математики: в 40 т. Т. 23: Клауди Альсина. Тысяча граней геометрической красоты. Многогранники. / Пер. с исп. – М.: Де Агостини, 2014. – 144 с. http://mnogogranniki.ru http://www.geometry2006.narod.ru/Lecture/SemRegPol/SemRegPol.htm http://geometry-and-art.ru/index.html https://tetraksis.com/glavnaya/polygon/polygon2 http://www.wikiwand.com/ru http://school-37.ru/downloads/poly/uniform/index.htm https://www.calc.ru/geom.html http://mathworld.wolfram.com/topics/ArchimedeanSolids.html